2.3. Метод контурних струмів

Для більш раціональних розрахунків використовують методи, в основу яких покладені закони Кірхгофа. Розглянемо метод контурних струмів на прикладі схеми, представленої на рис.2.3.

В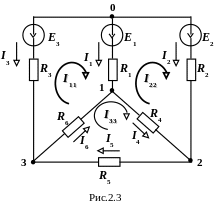 ибираємо три незалежних контури: 0–1–3–0; 0–1–2–0 та 1–2–3–1.

Припустимо, що в кожному контурі проходять контурні струми I₁₁, I₂₂ і I₃₃, спрямовані за годинниковою стрілкою.

Для кожного контуру складаємо рівняння за 2-м законом Кірхгофа. При цьому враховуємо, що в загальному розгалуженні незалежних контурів проходить струм, який дорівнює різниці контурних струмів, що протікають у цих контурах. Приймаємо напрями обходів контурів за годинниковою стрілкою.

Складаємо рівняння для контуру 0–1–3–0:

(R₁ + R₆ + R₃)I₁₁ – R₁I₂₂ – R₆I₃₃ = Е₁ – Е₃ .

Уводимо позначення:

R₁ + R₆ + R₃ = R₁₁ ;

–R₁ = R₁₂ ;

–R₆ = R₁₃ ;

Е₁ – Е₃ = Е₁₁ .

Тоді рівняння для контуру 0–1–3–0 буде мати вигляд:

R₁₁I₁₁ + R₁₂I₂₂ + R₁₃I₃₃ = Е₁₁ . (2.3)

Складаємо рівняння для контуру 0–1–2–0:

(R₁ + R₂ + R₄)I₂₂ – R₁I₁₁ – R₄I₃₃ = Е₂ – Е₁ .

Уводимо позначення:

R₁ + R₂ + R₄ = R₂₂ ;

–R₁ = R₂₁ ;

–R₄ = R₂₃ ;

Е₂ – Е₁ = Е₂₂ .

Тоді рівняння для контуру 0–1–2–0 буде мати вигляд:

R₂₁I₁₁ + R₂₂I₂₂ + R₂₃I₃₃ = Е₂₂ . (2.4)

Складаємо рівняння для контуру 1–2–3–1:

(R₄ + R₅ + R₆)I₃₃ – R₆I₁₁ – R₄I₂₂ = 0 .

Уводимо позначення:

R₄ + R₅ + R₆ = R₃₃ ;

–R₆ = R₃₁ ;

–R₄ = R₃₂ ;

0 = Е₃₃ .

Тоді рівняння для контуру 1–2–3–1 буде мати вигляд:

R₃₁I₁₁ + R₃₂I₂₂ + R₃₃I₃₃ = Е₃₃ . (2.5)

В отриманих рівняннях:

R₁₁, R₂₂, R₃₃ – повні або власні опори контурів;

R₁₂ = R₂₁, R₁₃ = R₃₁, R₂₃ = R₃₂ – опори загальних розгалужень контурів

(беруться зі знаком «+», якщо напрями контурних струмів у цьому розгалуженні збігаються, беруться зі знаком «–», якщо напрями контурних струмів у цьому розгалуженні не збігаються);

Е₁₁, Е₂₂, Е₃₃ – контурні е.р.с.,

які дорівнюють алгебраїчній сумі е.р.с. у відповідному контурі.

Вирішивши систему рівнянь (2.3), (2.4), (2.5), знаходимо контурні струми I₁₁, I₂₂, I₃₃, а після цього дійсні струми в розгалуженнях:

I₁ = I₁₁ – I₂₂ , I₂ = I₂₂ , I₃ = I₁₁ , I₄ = I₃₃ – I₂₂ , I₅ = I₃₃ , I₆ = I₃₃ – I₁₁.

Приклад 2.1

Для розрахункової схеми, приведеної на рис.2.2, задані наступні значення опорів і е.р.с.:

R₁ = 0,6 Ом ; R₄ = 2,0 Ом ; Е₁ = 10 В ;

R₂ = 1,2 Ом ; R₅ = 2,0 Ом ; Е₂ = 60 В ;

R₃ = 1,6 Ом ; R₆ = 1,0 Ом ; Е₃ = 40 В .

Розрахувати сили струмів у розгалуженнях.

Рішення.

Використовуємо рівняння (2.3), (2.4), (2.5) і знаходимо опори і е.р.с.:

R₁₁ = 3,2 Ом ; R₂₂ = 3,8 Ом ; R₃₃ = 5,0 Ом ;

R₁₂ = –0,6 Ом ; R₂₁ = –0,6 Ом ; R₃₁ = –1,0 Ом ;

R₁₃ = –1,0 Ом ; R₂₃ = –2,0 Ом ; R₃₂ = –2,0 Ом ;

Е₁₁ = –30 В ; Е₂₂ = 50 В ; Е₃₃ = 0 В .

Враховуючи отримані значення, запишемо систему рівнянь для розглядаємої схеми кола:

3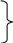 ,2I₁₁ – 0,6I₂₂ – 1I₃₃ = –30 ;

–0,6I₁₁ + 3,8I₂₂ – 2I₃₃ = 50 ;

–1I₁₁ – 2I₂₂ + 5I₃₃ = 0 .

Вирішуємо отриману систему рівнянь за допомогою визначників третього порядку. Знаходимо визначник системи:

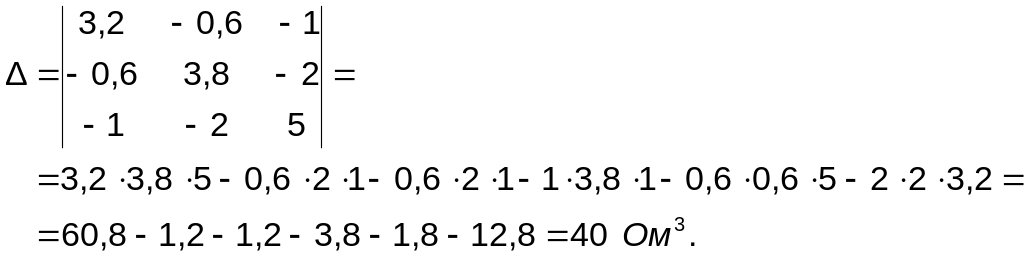
Знаходимо доповнення визначника:

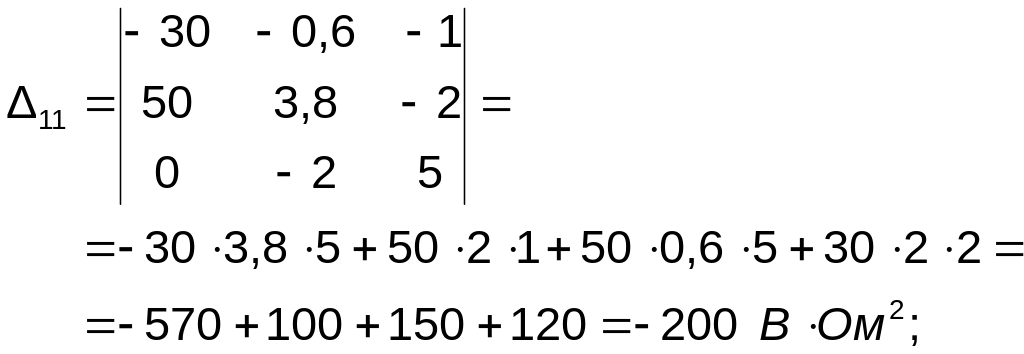
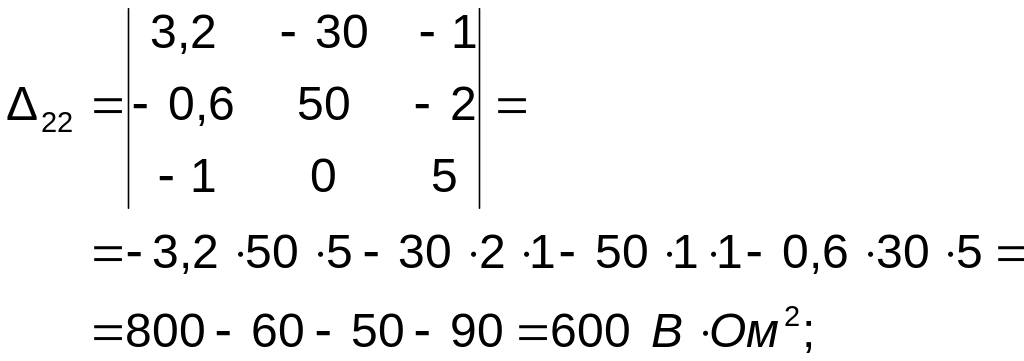
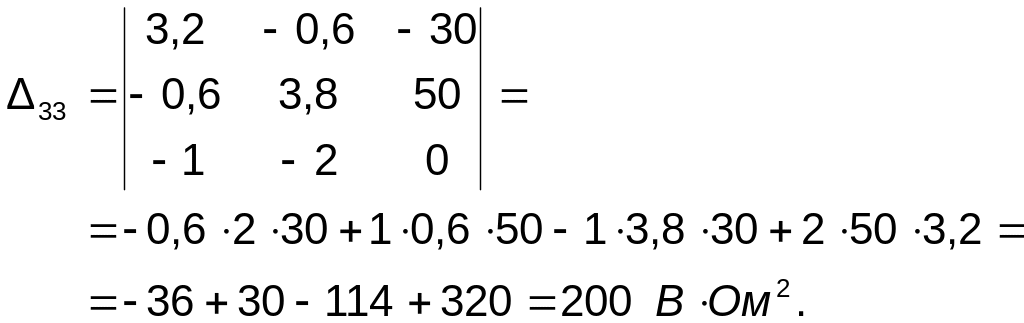
Визначаємо сили контурних струмів:

Визначаємо сили струмів у розгалуженнях схеми електричного кола:

I₁ = I₁₁ – I₂₂ = –5 – 15 = –20 А ;

I₂ = I₂₂ = 15 А ;

I₃ = –I₁₁ = 5 А ;

I₄ = I₃₃ – I₂₂ = 5 – 15 = –10 А ;

I₅ = I₃₃ = 5 А ;

I₆ = I₃₃ – I₁₁ = 5 – (–5) = 10 А .