41. Взаимная индукция

Возьмем два контура, расположенные недалеко друг от друга, как это показано на рисунке 5.4.

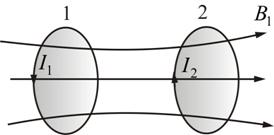
Рис. 5.4

      В первом контуре течет ток   . Он создает магнитный поток, который пронизывает и витки второго контура.

,

(5.3.1)

      При изменении тока    во втором контуре наводится ЭДС индукции:

,

(5.3.2)

      Аналогично, ток    второго контура создает магнитный поток, пронизывающий первый контур:

,

(5.3.3)

      И при изменении тока    наводится ЭДС:

,

(5.3.4)

      Контуры называются связанными, а явление – взаимной индукцией. Коэффициенты    и    называются взаимной индуктивностью, или коэффициентами взаимной индукции. Причём 

42. Токи при размыкании и замыкании цепи.

При всяком изменении силы тока в проводящем контуре возникает э. д. с. самоиндукции, в результате чего в контуре появляются дополнительные токи, называемые экстратоками самоиндукции. Экстратоки самоиндукции, согласно правилу Ленца, всегда направлены так, чтобы препятствовать изменениям тока в цепи, т. е. направлены противоположно току, создаваемому источником. При выключении источника тока экстратоки имеют такое же направление, что и ослабевающий ток. Следовательно, наличие индуктивности в цепи приводит к замедлению исчезновения или установления тока в цепи.

Размыкание:

Под действием внешней э. д. с. в цепи течет постоянный ток

В момент времени t=0 отключим источник тока. Ток в катушке индуктивностью L начнет уменьшаться, что приведет к возникновению э.д.с. самоиндукции   препятствующей, согласно правилу Ленца, уменьшению тока. В каждый момент време­ни ток в цепи определяется законом Ома I= _s/R, или

Разделив в выражении (127.1) переменные, получим   Интегрируя это уравнение по I (от I₀ до I) и t (от 0 до t), находим ln (I /I₀) = –Rt/L, или где t=L/R — постоянная, называемая временем релаксации.

Замыкание:

В момент замыкания (t=0) сила тока I = 0 и u = –  . Следовательно, интегрируя по и (от –  до IR– ) и t (от 0 до t), находим ln[(IR– )]/–  = —t/t, или

                                                        (127.3)

где   — установившийся ток (при t®¥).

1- размыкание, 2 - замыкание

       

43. Энергия магнитного поля электрического тока

Рассмотрим контур индуктивностью L, по которому течет ток I. С данным контуром сцеплен магнитный поток (см. (126.1)) Ф=LI, причем при изменении тока на dIмагнитный поток изменяется на dФ=LdI. Однако для изменения магнитного потока на величину dФ (см. § 121) необходимо совершить работу dА=IdФ=LIdI. Тогда работа по созданию магнитного потока Ф будет равна

Следовательно, энергия магнитного поля, связанного с контуром,

 

Энергию магнитного поля можно представить как функцию величин, характеризу­ющих это поле в окружающем пространстве. Для этого рассмотрим частный слу­чай — однородное магнитное поле внутри длинного соленоида. Подставив в формулу (130.1) выражение (126.2), получим

Так как I=Bl/(m₀mN) (см. (119.2)) и В=m₀mH (см. (109.3)), то

                                                          (130.2)

где Sl = V — объем соленоида.

Магнитное поле соленоида однородно и сосредоточено внутри него, поэтому энергия (см. (130.2)) заключена в объеме соленоида и распределена в нем с постоянной объемной плотностью