МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«тюменский государственный нефтегазовый университет»

Институт кибернетики, информатики и связи

отделение информационных технологий и вычислительной техники

МАТЕМАТИКА

методические рекомендации

для самостоятельной работы студентов

специальностей

230115 Программирование в компьютерных системах

230401 Информационные системы (по отраслям)

210709 Многоканальные телекоммуникационные системы

210721 Радиосвязь, радиовещание и телевидение

Тюмень

ТюмГНГУ

2012

СОДЕРЖАНИЕ

ОБЩИЕ ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ 5

САМОСТОЯТЕЛЬНЫХ РАБОТ 5

САМОСТОЯТЕЛЬНАЯ РАБОТА №1 5

САМОСТОЯТЕЛЬНАЯ РАБОТА №2 11

САМОСТОЯТЕЛЬНАЯ РАБОТА №3 12

САМОСТОЯТЕЛЬНАЯ РАБОТА №4 13

САМОСТОЯТЕЛЬНАЯ РАБОТА №5 14

САМОСТОЯТЕЛЬНАЯ РАБОТА №6 16

САМОСТОЯТЕЛЬНАЯ РАБОТА №7 19

САМОСТОЯТЕЛЬНАЯ РАБОТА №8 20

САМОСТОЯТЕЛЬНАЯ РАБОТА №9 21

САМОСТОЯТЕЛЬНАЯ РАБОТА №10 22

САМОСТОЯТЕЛЬНАЯ РАБОТА №11 24

САМОСТОЯТЕЛЬНАЯ РАБОТА №12 25

САМОСТОЯТЕЛЬНАЯ РАБОТА №13 27

САМОСТОЯТЕЛЬНАЯ РАБОТА №14 29

СПИСОК ЛИТЕРАТУРЫ 32

Пояснительная записка

Методические рекомендации по выполнению самостоятельных работ составлены в соответствии с программой учебной дисциплины «Математика» для студентов, обучающихся по специальностям 230115 Программирование в компьютерных системах, 230401 Информационные системы (по отраслям) на базе основного общего образования, 210709 Многоканальные телекоммуникационные системы, 210721 Радиосвязь, радиовещание и телевидение.

Целями выполнения самостоятельных работ студентами является:

• систематизация, закрепление, расширение теоретических знаний и применение их для решения конкретных задач;

• выявление уровня подготовки студентов к самостоятельному решению профессиональных задач;

• формирование умений использовать справочную документацию и специальную литературу;

• развитие познавательных способностей и активности студентов, творческой инициативы, самостоятельности, ответственности и организованности;

• развитие навыков организации самостоятельной работы.

Основными видами заданий для внеаудиторной самостоятельной работы является:

• повторение теоретического материала через рассмотрение примеров решений задач;

• подготовка к практическим работам;

• решение задач и уравнений по основным темам.

Методические рекомендации содержат пояснительную записку, общие требования к оформлению самостоятельных работ, критерии оценки самостоятельные работ, описания каждой работы, которые снабжены пояснениями к изучаемым вопросам, примерами решения задач и заданиями для самостоятельного решения, ссылками на рекомендуемую литературу.

Сроки выполнения самостоятельных работ определяются в соответствии с календарно – тематическим планом дисциплины. На выполнение каждой работы отводится определенное количество часов в соответствии с тематическим планом программы учебной дисциплины «Математика».

Методические рекомендации окажут помощь преподавателям в организации самостоятельной работы студентов, а также будут необходимы студентам при повторении изученного материала и подготовке к зачету и экзамену.

Общие требования к оформлению самостоятельных работ

Самостоятельные работы требуется выполнять в отдельной ученической тетради для самостоятельных работ. Каждая работа должна содержать:

• номер и тему самостоятельной работы;

• цель работы;

• условия заданий;

• подробное решение заданий.

Самостоятельная работа №1

Тема: Решение задач на тему «Корни, степени и логарифмы»

Цель: закрепление умений решения логарифмических и степенных уравнений.

Время выполнения: 8 часов

Теоретические сведения

Степенная функция - функция вида , где  - заданное число, называемое показателем степени. Иногда степенной функцией называется функция несколько более общего вида .

Многие функциональные зависимости выражаются через степенную функцию. Например, объем куба  есть степенная функция от  (длины его ребра): ; период  колебаний математического маятника пропорционален длине маятника  в степени , а именно . Если газ расширяется или сжимается без теплообмена с окружающей средой, то его давление  и объем  связаны формулой  (для воздуха, например, ). Заметим, что в двух последних случаях показатель не является целым числом.

При любом показателе степени  показательная функция  определена во всяком случае на положительной полуоси. Свойства степенной функции различны в зависимости от значения показателя степени. Если  - натуральное число , то функция  определена на всей числовой оси, обращается в нуль при , четная при четном  и нечетная при  нечетном, неограниченно возрастает при безграничном возрастании аргумента . На Рисунок 1 и 2 приведены графики типичных степенных функций с целым положительным показателем:  (кубическая парабола) и  (парабола четвертой степени). При  степенная функция  является линейной функцией, при  - квадратичной функцией .

Рисунок 1

Рисунок 2

Если  - отрицательное целое число , то степенная функция определяется равенством . Она определена при всех отличных от нуля . Ее график состоит из двух частей (ветвей), имеющих асимптотами оси координат, к которым эти кривые неограниченно приближаются. Типичные представители - функции  и  их графики даны на Рисунок 3 и 4. При  по определению . Если , то функция  (обозначается также ) определяется как обратная функция для функции . При четном  функция определена лишь для , а при нечетном  - на всей оси. Графики таких функций  и изображены на Рис. 5 и 6.

Рисунок 3

Рисунок 4

Рисунок 5

Рисунок 6

Для рационального показателя  ( - несократимая дробь) степенная функция определяется формулой

.

Графики типичных степенных функций с рациональным показателем приведены на Рис. 7, 8, 9.

Рисунок 7

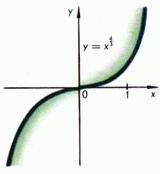
Рисунок 8

Рисунок 9

Логарифм – это число, применение которого позволяет упростить многие сложные операции арифметики. Использование в вычислениях вместо чисел их логарифмов позволяет заменить умножение более простой операцией сложения, деление - вычитанием, возведение в степень - умножением и извлечение корней - делением. Общее описание. Логарифмом данного числа называется показатель степени, в которую нужно возвести другое число, называемое основанием логарифма, чтобы получить данное число. Например, логарифм числа 100 по основанию 10 равен 2. Иначе говоря, 10 нужно возвести в квадрат, чтобы получить число 100 (102 = 100). Если n - заданное число, b - основание и l - логарифм, то bl = n. Число n также называется антилогарифмом по основанию b числа l. Например, антилогарифм 2 по основанию 10 равен 100. Сказанное можно записать в виде соотношений logb n = l и antilogb l = n. Основные свойства логарифмов:

Любое положительное число, кроме единицы, может служить основанием логарифмов, но, к сожалению, оказывается, что если b и n - рациональные числа, то в редких случаях найдется такое рациональное число l, что bl = n. Однако можно определить иррациональное число l, например, такое, что 10l = 2; это иррациональное число l можно с любой требуемой точностью приблизить рациональными числами. Оказывается, что в приведенном примере l примерно равно 0,3010, и это приближенное значение логарифма по основанию 10 числа 2 можно найти в четырехзначных таблицах десятичных логарифмов. Логарифмы по основанию 10 (или десятичные логарифмы) столь часто используются при вычислениях, что их называют обычными логарифмами и записывают в виде log2 = 0,3010 или lg2 = 0,3010, опуская явное указание основания логарифма. Логарифмы по основанию e, трансцендентному числу, приближенно равному 2,71828, называются натуральными логарифмами. Они встречаются преимущественно в работах по математическому анализу и его приложениям к различным наукам. Натуральные логарифмы также записывают, не указывая явно основание, но используя специальное обозначение ln: например, ln2 = 0,6931, т.к. e0,6931 = 2.

Пользование таблицами обычных логарифмов. Обычный логарифм числа - это показатель степени, в которую нужно возвести 10, чтобы получить данное число. Так как 100 = 1, 101 = 10 и 102 = 100, мы сразу получаем, что log1 = 0, log10 = 1, log100 = 2 и т.д. для возрастающих целых степеней 10. Аналогично, 10-1 = 0,1, 10-2 = 0,01 и, следовательно, log0,1 = -1, log0,01 = -2 и т.д. для всех целых отрицательных степеней 10. Обычные логарифмы остальных чисел заключены между логарифмами ближайших к ним целых степеней числа 10; log2 должен быть заключен между 0 и 1, log20 - между 1 и 2, а log0,2 - между -1 и 0. Таким образом, логарифм состоит из двух частей, целого числа и десятичной дроби, заключенной между 0 и 1. Целочисленная часть называется характеристикой логарифма и определяется по самому числу, дробная часть называется мантиссой и может быть найдена из таблиц. Кроме того, log20 = log(2ґ10) = log2 + log10 = (log2) + 1. Логарифм числа 2 равен 0,3010, поэтому log20 = 0,3010 + 1 = 1,3010. Аналогично, log0,2 = log(2е10) = log2 - log10 = (log2) - 1 = 0,3010 - 1. Выполнив вычитание, мы получим log0,2 = - 0,6990. Однако удобнее представить log0,2 в виде 0,3010 - 1 или как 9,3010 - 10; можно сформулировать и общее правило: все числа, получающиеся из данного числа умножением на степень числа 10, имеют одинаковые мантиссы, равные мантиссе заданного числа. В большинстве таблиц приведены мантиссы чисел, лежащих в интервале от 1 до 10, поскольку мантиссы всех остальных чисел могут быть получены из приведенных в таблице. В большинстве таблиц логарифмы даются с четырьмя или пятью десятичными знаками, хотя существуют семизначные таблицы и таблицы с еще большим числом знаков. Научиться пользоваться такими таблицами легче всего на примерах. Чтобы найти log3,59, прежде всего заметим, что число 3,59 заключено между 100 и 101, поэтому его характеристика равна 0. Находим в таблице число 35 (слева) и движемся по строке до столбца, у которого сверху стоит число 9; на пересечении этого столбца и строки 35 стоит число 5551, поэтому log3,59 = 0,5551. Чтобы найти мантиссу числа с четырьмя значащими цифрами, необходимо прибегнуть к интерполяции. В некоторых таблицах интерполирование облегчается пропорциональными частями, приведенными в последних девяти столбцах в правой части каждой страницы таблиц. Найдем теперь log736,4; число 736,4 лежит между 102 и 103, поэтому характеристика его логарифма равна 2. В таблице находим строку, слева от которой стоит 73 и столбец 6. На пересечении этой строки и этого столбца стоит число 8669. Среди линейных частей находим столбец 4. На пересечении строки 73 и столбца 4 стоит число 2. Прибавив 2 к 8669, получим мантиссу - она равна 8671. Таким образом, log736,4 = 2,8671.

Натуральные логарифмы. Таблицы и свойства натуральных логарифмов аналогичны таблицам и свойствам обычных логарифмов. Основное различие между теми и другими состоит в том, что целочисленная часть натурального логарифма не имеет существенного значения при определении положения десятичной запятой, и поэтому различие между мантиссой и характеристикой не играет особой роли. Натуральные логарифмы чисел 5,432; 54,32 и 543,2 равны, соответственно, 1,6923; 3,9949 и 6,2975. Взаимосвязь между этими логарифмами станет очевидной, если рассмотреть разности между ними: log543,2 - log54,32 = 6,2975 - 3,9949 = 2,3026; последнее число есть не что иное, как натуральный логарифм числа 10 (пишется так: ln10); log543,2 - log5,432 = 4,6052; последнее число равно 2ln10. Но 543,2 = 10*54,32 = 102*5,432. Таким образом, по натуральному логарифму данного числа a можно найти натуральные логарифмы чисел, равные произведениям числа a на любые степени n числа 10, если к lna прибавлять ln10, умноженный на n, т.е. ln(a*10n) = lna + nln10 = lna + 2,3026n. Например, ln0,005432 = ln(5,432*10-3) = ln5,432 - 3ln10 = 1,6923 - (3*2,3026) = - 5,2155. Поэтому таблицы натуральных логарифмов, как и таблицы обычных логарифмов, обычно содержат только логарифмы чисел от 1 до 10. В системе натуральных логарифмов можно говорить об антилогарифмах, но чаще говорят об экспоненциальной функции или об экспоненте. Если x = lny, то y = ex, и y называется экспонентой от x (для удобства типографского набора часто пишут y = exp x). Экспонента играет роль антилогарифма числа x. С помощью таблиц десятичных и натуральных логарифмов можно составить таблицы логарифмов по любому основанию, отличному от 10 и e. Если logb a = x, то bx = a, и, следовательно, logc bx = logc a или xlogc b = logc a, или x = logc a/logc b = logb a. Следовательно, с помощью этой формулы обращения из таблицы логарифмов по основанию c можно построить таблицы логарифмов по любому другому основанию b. Множитель 1/logc b называется модулем перехода от основания c к основанию b. Ничто не мешает, например, пользуясь формулой обращения, или перехода от одной системы логарифмов к другой, найти натуральные логарифмы по таблице обычных логарифмов или совершить обратный переход. Например, log105,432 = loge 5,432/loge 10 = 1,6923/2,3026 = 1,6923ґ0,4343 = 0,7350. Число 0,4343, на которое нужно умножить натуральный логарифм данного числа, чтобы получить обычный логарифм, является модулем перехода к системе обычных логарифмов.