3. Элементарная алгебра

Приведены некоторые функции которые могут быть использованы при решении задач элементарной алгебры

Solvelhs==rhs,x решает относительно переменной x уравнение lhs = rhs;

NSolvelhs==rhs,x  решает численно относительно переменной x уравнение lhs = rhs;

Solve{lhs₁==rhs₁,lhs₂==rhs₂,…},{x,y,…}  решает относительно переменных x, у,… систему уравнений lhs₁=rhs₁, lhs₂=rhs₂,…;

Reduce[неравенство,x] – решает относительно переменной x данное неравенство;

Factorвыражение  представляет в виде произведения данное выражение;

Simplify% Упрощает выражение полученное в предыдущем примере;

Simplifyвыражение  Упрощает данное выражение;

Factorмногочлен с целыми коэффициэнтами  представляет в виде произведения многочленов с целыми коэффициентами; FactorListpolinom  определяет множители многочлена и показатели их степеней;

...

Пример 3.1. Решить уравнение .

Решение. Набираем Solve и Enter цифрогого блока . На экран выводится  :

In1 := Solve

Out1={{x22i},{x-2+2i},{x1},{x4}}.

Получены четыре решения: x₁ = 22i, x₂ = 2+2i, x₃ = 1, x₄ = 4.

Пример 3.2. Решить неравенство .

Решение. Набираем Reduce и Enter цифрогого блока . На экран выводится  :

In[2]:=Reduce

Out[2]= 4  x  0.

Пример 3.3. Разложить на произведение сомножителей с целыми коэффициентами выражение .

Решение. Набираем Scriem Factor[ ]и Enter цифрогого блока . На экран выводится  :

In[3] := Factor[ ]

Out[3]=(1+x)(1+x)(1x+x²x³+x⁴)(1+x+x²+x³+x⁴).

Пример 3.4. Упростить выражение полученное в предыдущем примере

Решение. Набираем Simplify[%]и Enter цифрогого блока . На экран выводится  :

In[4]:= Simplify[%]

Out[4]= .

Пример 3.5. Решить уравнение : 1) в точном виде; 2) численно (приближенно).

Решение. 1) Набираем Solve и Enter цифрогого блока . На экран выводится  :

In[5]:= Solve

Out[5]={{x1},{xi},{xi}}.

2) Набираем NSolve и Enter цифрогого блока . На экран выводится  :

In[6]:= NSolve

Out[6]={{x1},{x7.124510^19+1.i},{x7.124510^191.i}.

Получили различные результаты, но которые отличаются очень мало друг от друга.

Примеры для индивидуального решения

E.3.1. Разложить в прозведение выражение xⁿ1, где n равен 10 плюс номер варианта.

E.3.2. Упростить выражение полученное в предыдущем примере.

 

E.3.3.Решить уравнение  P(x) = 0, где P(x) многочлен из Matematica I, ex.3.7.4, стр.150.

E.3.4. Решить неравенство из Matematica I, ex.3.7.7, стр.152.

4. Примеры из линейной алгебры

Матрицы могут быть обозначены через A, B, M, a, b, m, … и они не должны быть обозначены через C, D. матрица вводится в виде списка, элементы которого списки содержащие элементы линий данной матрицыe. Напрмер, квадратная матрица третьего порядка A= вводится следующим образом : A:={{a₁₁,a₁₂,a₁₃},{a₂₁,a₂₂,a₂₃},{a₃₁,a₃₂,a₃₃}} и нажимаем Shift+Enter или Enter цифрогого блока . На экран выводится  :

In[1]:=A:={{a₁,a₁₂,a₁₃},{a₂₁,a₂₂,a₂₃},{a₃₁,a₃₂,a₃₃}}.

С матрицей введенной в такой форме могут быть произведены все необходимые операции. Если хотим представить матрицу в привычную форму то набираем MatrixFormA нажимаем Shift+Enter или Enter цифрогого блока . На экран выводится  :

Out[1]//MatrixForm[A]=

.

Среди функций линейной алгебры можно отметить:

DetA  вычисляет определитель матрицы А.

DotA,B  вычисляет произведение матриц А и В и выводит результат в виде списка;

InverseA  вычисляет обратную матрицу для данной матрицы A и выводит результат в виде списка;

TransposeA  вычисляет транспонированную матрицу для данной матрицы A и выводит результат в виде списка;

EigenvaluesA  вычисляет A şi le afişează în formă de listă;

EigenvectorsA  вычисляет собственные значения матрицы A и выводит результат в виде списка;

EigensystemA  вычисляет собственные значения и собственные вектора матрицы A и выводит результат в виде списка первый элемент которго список собственных значений а остальные элементы – списки координат собственных векторов;

MatrixFormA.B  выводит произведение AB матриц A и B в виде матрицы;

MatrixFormA+B  выводит сумму A+B матриц A и B в виде матрицы;

MatrixForm*A  выводит произведение числа  на матрицу A в виде матрицы;

TransposeA//MatrixForm  выводит в виде матрицы транспонированную матрицу;

InverseA//MatrixForm  выводит в виде матрицы обратную матрицу;

…

Пример4.1.Рассмотрим матрицы 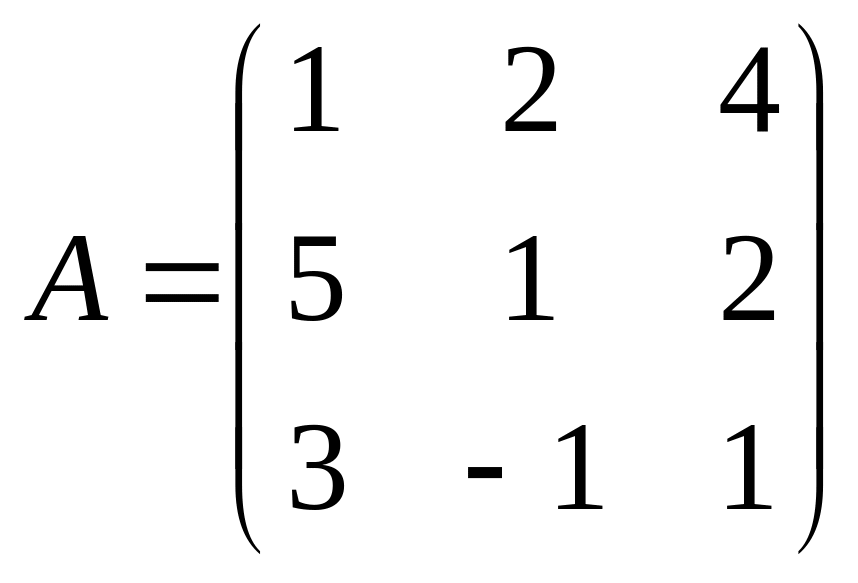, 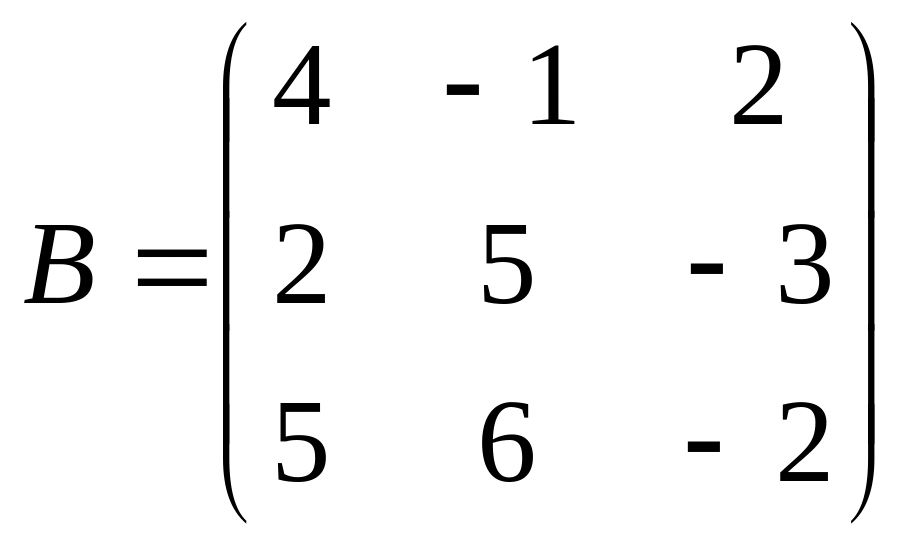и число3.Найти: 1) A+B; 2) 3A; 3) AB; 4) detA; 5) A^1; 6) A^T.

Решение. Вводим матрицы A и B. Набираем A:={{1,2 ,4 },{5,1 ,2 },{3,-1 ,1 }}, нажимаем Shift+Enter или Enter цифрогого блока . На экран выводится  :

In1 :=A:={{1,2 ,4 },{5,1 ,2 },{3,-1 ,1 }}.

Аналогично B:={{4,1 ,2 },{2,5 ,3 },{5,6 ,2 }}, нажимаем Shift+Enter или Enter цифрогого блока . На экран выводится  :

In2 :=B:={{4,1 ,2 },{2,5 ,3 },{5,6 ,2 }}.

Следовательно матрцы A и B введены в документ

1) Для вычисления суммы A+B набираем MatrixFormA+B, нажимаем Shift+Enter или Enter цифрогого блока . На экран выводится  :

In3 :=MatrixFormA+B,

Out3//MatrixForm=

,

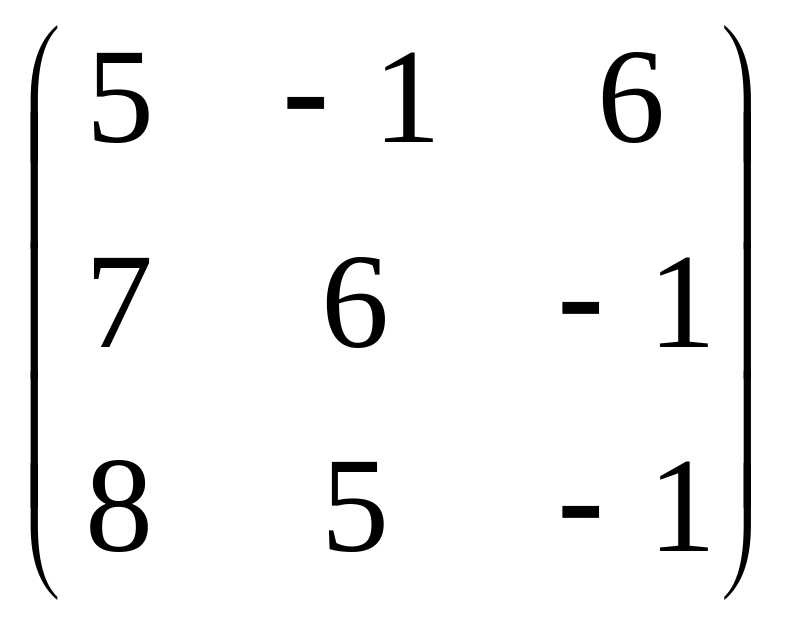2) Для вычисления произведения 3A набираем MatrixForm3*A, нажимаем Shift+Enter или Enter цифрогого блока . На экран выводится 

In4 :=MatrixForm3*A,

Out4//MatrixForm=

.

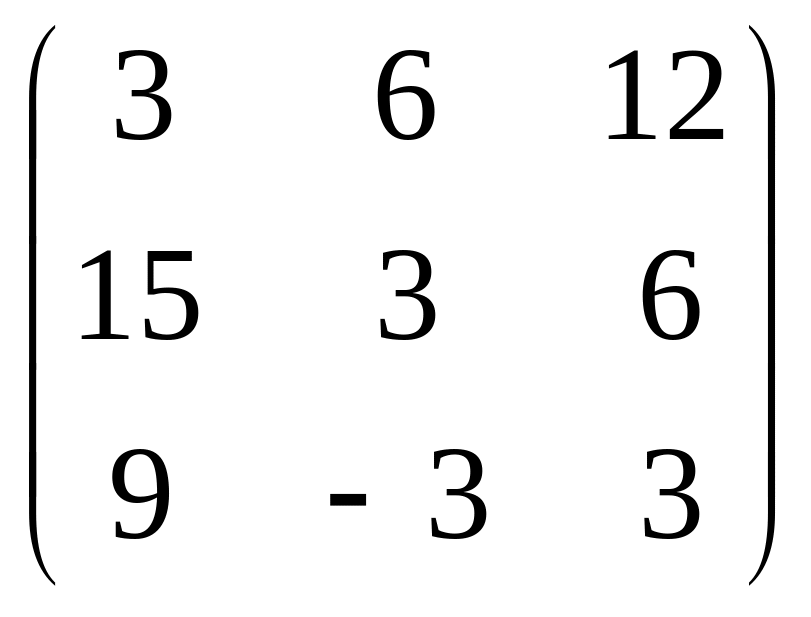3)  Для вычисления произведения AВ набираем MatrixFormA.В, нажимаем Shift+Enter или Enter цифрогого блока . На экран выводится 

In5 :=MatrixFormA.B,

Out5//MatrixForm=

.

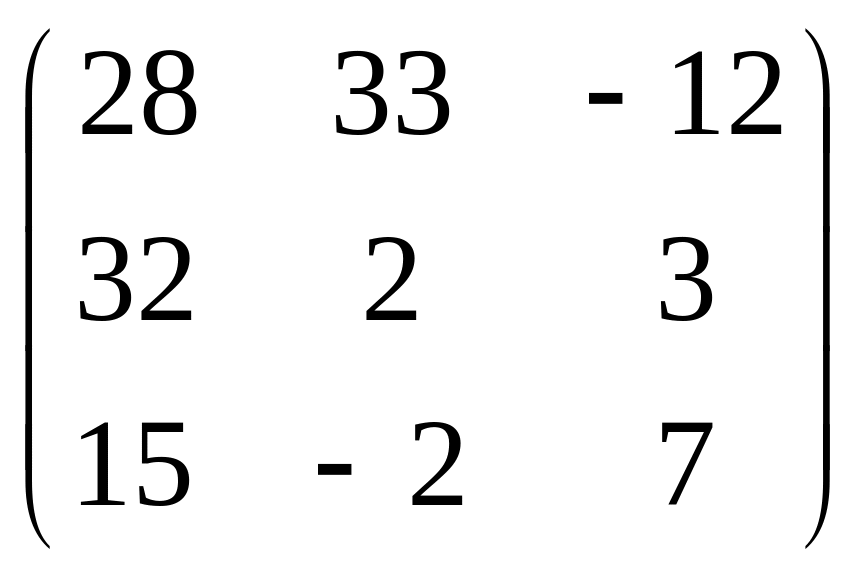4) Для вычисления определителя матрицы A набираем DetA нажимаем Shift+Enter или Enter цифрогого блока . На экран выводится 

In6 :=DetA

Out6=27.

5) Для вычисления матрицы обратной матрицы A набираем InverseA//MatrixForm нажимаем Shift+Enter или Enter цифрогого блока . На экран выводится 

In7 :=InverseA//MatrixForm

Out7=MatrixForm=

.

6) Для вычисления матрицы транспонированной матрице A набираем TranspozeA//MatrixForm нажимаем Shift+Enter или Enter цифрогого блока . На экран выводится  In8 :=TransposeA//MatrixForm

Out8=MatrixForm=

.

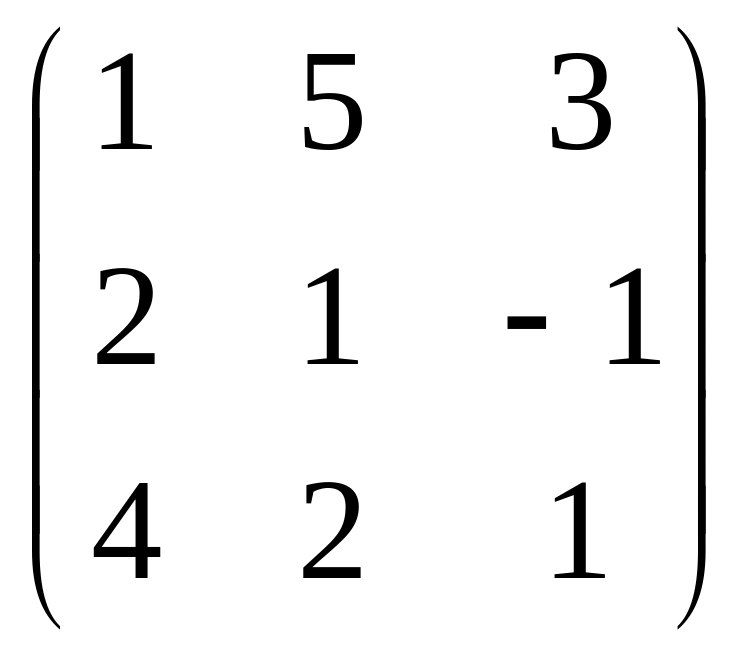Примечание. Известно что умножение чисел обозначается значком *. Если обозначить умножение матрц таким же знаком, тогда не получаем произведение матриц а матрицу элементы которой равны произведению соответствующих элементов данных матриц

Пример:Если наберем MatrixForm[A*B] нажимаем Shift+Enter или Enter цифрогого блока . На экран выводится 

In[9] :=MatrixForm[A*B]

Out[9]//MatrixForm=

.

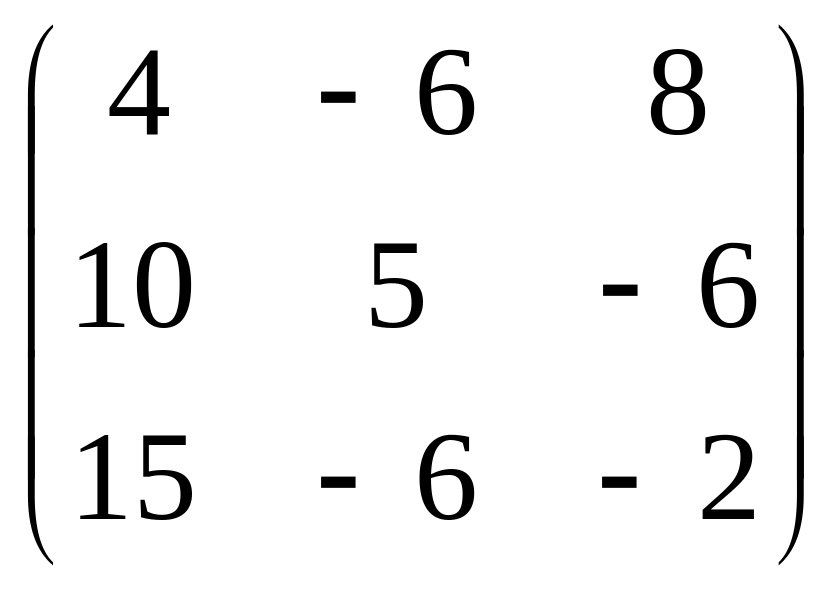Пример 4.2. Для матрицы M= , найти: 1) собственные значения ; 2) собственные вектора; 3) собственные значения и собственные вектора.

Решение. Вводим матрицу M. Набираем M:={{1,3,1},{3,5,1},{3,3,1}} и нажимаем Shift+Enter или Enter цифрогого блока . На экран выводится 

In10:=M:={{-1,3,-1},{-3,5,-1},{-3,3,1}}. .

1. Для нахождения собственных значения матрицы М набираем EigenvaluesM и нажимаем Shift+Enter

2. In10:=EigenvaluesM

Out10={2,2,1}.

3. Для нахождения собственных векторов матрицы М набираем EigenvectorsM и Shift+Enter.

4. In11:=EigenvectorsM

Out11={{-1,0,3},{1,1,0},{1,1,1}}.

3) Для нахождения собственных значений и собственных векторов набираем EigensystemM и Shift+Enter.

In12:=EigensystemM

Out11={{2,2,1},{-1,0,3},{1,1,0},{1,1,1}}.

Пример 4.3. Решить систему линейных уравнений

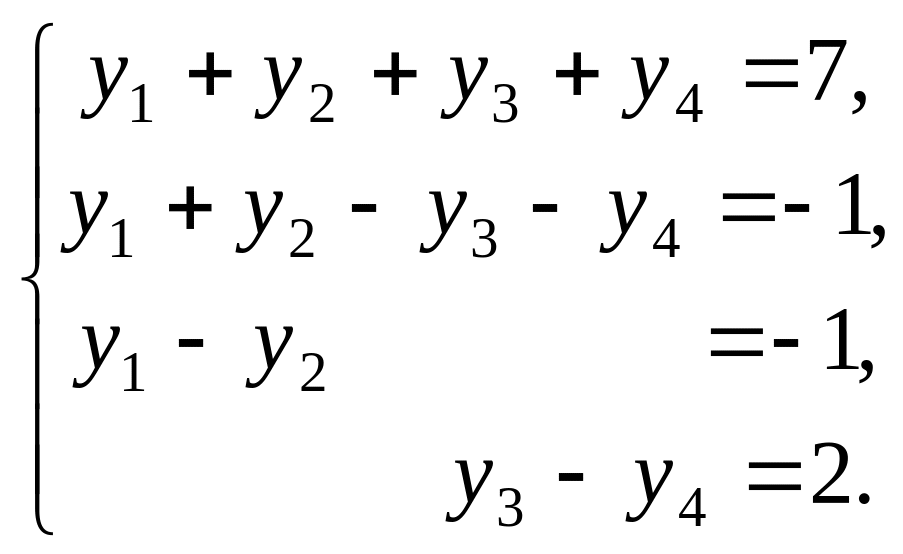
Решение. Набираем Solve{y₁+y₂+y₃+y₄==7, y₁+y₂y₃y₄==1, y₁y₂==1, y₃y₄==2}, {y₁,y₂,y₃,y₄} и Shift+Enter.

In[13]:= Solve{y₁+y₂+y₃+y₄==7, y₁+y₂y₃y₄==1, y₁y₂==1, y₃y₄==2}, {y₁,y₂,y₃,y₄}

Out[13]={{y₁1,y₂2,y₃3,y₄1}}.

Exemplul 4.4. Решить систему линейных уравнений

Rezolvare. Набираем Solve{2x₁+3x₂x₃==8, 5x₁2x₂+2x₃==6, x₁+4x₂3x₃==9},{x₁,x₂,x₃} şi и Shift+Enter.

In[13]:=Solve{2x₁+3x₂x₃==8,5x₁2x₂+2x₃==6,x₁+4x₂3x₃==9},{x₁,x₂,x₃}

Out[13]={{x₁2,x₂1,x₃1}}.

Получено решение x₁=2, x₂=1,x₃=1.

Примеры для индивидуального решения

E.4.1. Даны две матрицы A и B и число из Matematica I, пр. 4.6.1, стр.189, найти: 1)A ; 2)A+B ; 3)AB ; 4)detA ; 5)A^1.

E.4.2. Решить систему линейных уравнений из Matematica I, пр. 4.6.4, стр.197.