4.1.2. Элементы аналитической геометрии на плоскости

Простейшие задачи на плоскости

1. Расстояние между двумя точками и вычисляется по формуле:

.

2. Если и , то координаты точки , делящей направленный отрезок в отношении , вычисляются по формулам:

, .

В частности, если точка делит отрезок пополам ( ), то

, .

Различные виды уравнения прямой на плоскости

1. Углом наклона прямой к оси Ох называется наименьший положительный угол  (0   < ), на который надо повернуть против часовой стрелки ось Ох до совмещения с данной прямой.

Угловым коэффициентом прямой называется число k = tg .

2. Уравнение прямой, проходящей через данную точку в данном направлении :

.

3. Уравнение прямой с угловым коэффициентом:

.

4. Уравнение прямой, проходящей через две данные точки и :

.

Угловой коэффициент такой прямой можно вычислить по формуле:

.

5. Уравнение прямой в отрезках на осях:

,

где параметры a и b равны величинам отрезков, которые прямая отсекает от оси Ox и Oy соответственно.

6. Нормальное уравнение прямой:

,

где параметр p > 0 равен длине нормали, проведенной к прямой из начала координат,  – угол между нормалью и положительной частью оси Ox.

7. Общее уравнение прямой:

,

где A и B одновременно не равны нулю.

8. Чтобы общее уравнение прямой привести к нормальному уравнению, нужно общее уравнение умножить на нормирующий множитель . Знак перед корнем выбирается противоположным знаку коэффициента в общем уравнении.

Расстояние от точки до прямой на плоскости

Расстояние от точки до прямой вычисляется по формуле:

.

Взаимное расположение двух прямых на плоскости

1. Угол между двумя прямыми и вычисляется по формуле:

.

2. Условие параллельности двух прямых: прямые и параллельны тогда и только тогда, когда

.

3. Условие перпендикулярности двух прямых: прямые и перпендикулярны тогда и только тогда, когда

.

Кривые второго порядка

1. Окружностью радиуса R с центром в точке C(a; b) называется геометрическое место точек плоскости, для которых расстояние до центра С равно R. Каноническое уравнение окружности с центром в точке и радиусом (рис. 1): .

Рис. 1

2. Параболой называется геометрическое место точек плоскости, одинаково удаленных от данной точки F, называемой фокусом и от прямой, называемой директрисой. Если фокус взять в точке , а директрису задать уравнением , где p > 0, то получим параболу (рис. 2), каноническое уравнение которой имеет вид: .

Рис. 2

Если фокусы и директрисы брать тремя другими способами, то получим еще три параболы (табл. 1).

Таблица 1

Уравнение параболы	Фокус	Директриса

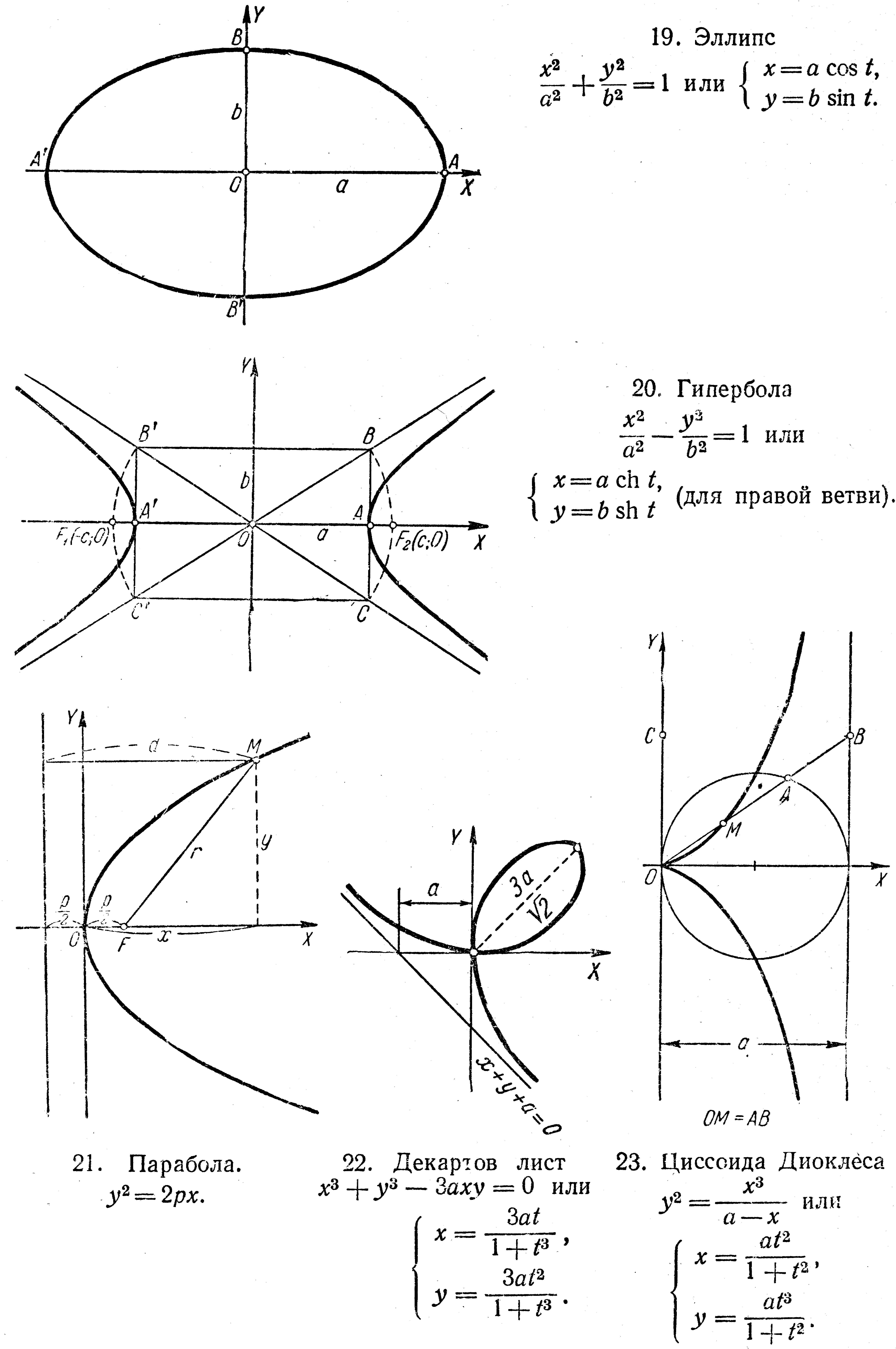
3. Эллипсом называется геометрическое место точек плоскости, сумма расстояний от которых до двух данных точек F₁ и F₂, называемых фокусами (|F₁F₂| = 2c) есть величина постоянная, равная 2a > 2c.

Каноническое уравнение эллипса (рис. 3):

.

Точки , , и – вершины эллипса; отрезок – большая ось, отрезок – малая ось; параметры и – большая и малая полуоси; точки и – левый и правый фокусы; число – эксцентриситет; и – левый и правый фокальные радиусы. Параметры , и связаны равенством .

Рис. 3

4. Гиперболой называется геометрическое место точек плоскости, разность расстояний от которых до двух данных точек F₁ и F₂, называемых фокусами (|F₁F₂| = 2c) есть величина постоянная, равная  2a, где 2a < 2c.

Каноническое уравнение гиперболы (рис. 4):

.

Точки и – вершины гиперболы; отрезок – действительная ось, отрезок – мнимая ось; параметры и – действительная и мнимая полуоси; точки и – левый и правый фокусы; число – эксцентриситет гиперболы; левый и правый фокальные радиусы для точек левой ветви гиперболы равны и , а для точек правой ветви гиперболы – это и ; прямые и – асимптоты гиперболы. Параметры , и связаны равенством .

Рис. 4