1.5.4 Решение слау методом обратной матрицы (ms Exсel)

Шаг 1. Ввод исходных данных.

В диапазон B2:F6 ввести матрицу коэффициентов при неизвестных, в диапазон G2:G6 ввести вектор свободных членов.

Шаг 2. Определение обратной матрицы.

Выделить диапазон B8:F12 ввести в него формулу =МОБР(B2:F6).

Завершить ввод формулы нажатием сочетания клавиш Ctrl+Shift+Enter.

Шаг 3. Определение значений параметров х_i.

Выделить диапазон B14:B18 ввести в него формулу =МУМНОЖ(B8:F12;G2:G6).

Завершить ввод формулы нажатием сочетания клавиш Ctrl+Shift+Enter.

Шаг 4. Проверка.

Выделяем диапазон ячеек D14:D18, записываем в этот диапазон формулу = МУМНОЖ(B2:F6;B14:B18).

Завершаем ввод формулы нажатием сочетанием клавиш Ctrl+Shift+Enter.

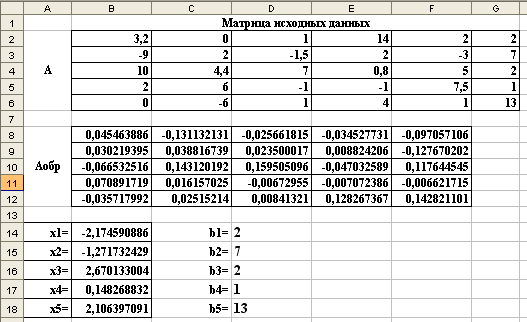
Рисунок 3 – Решение СЛАУ методом обратной матрицы

Полученные значения переменных b1, b2, b3, b4, b5 равны исходным значениям свободных членов системы уравнений.

Результаты решения задачи методом «Обратной матрицы» представлены на рисунке 3.

1.5.5 Решение слау в MathCad (Гаусс)

Рисунок 4 – Решение СЛАУ (Гаусс)

* Номер первой строки (столбца) матрицы или первого компонента вектора хранится в MathCAD в переменной ORIGIN.

Augment(A, В) формирует матрицу, в первых столбцах которой содержится матрица А, а в последних - матрица В (матрицы А и В должны иметь одинаковое число строк).

Rref(A) предназначена для приведения матрицы к ступенчатому виду с единичным базисным минором (выполняются элементарные операции со строками матрицы).

Шаг 1. Присваиваем переменной ORIGIN значение, равное единице.

Шаг 2. Вводим матрицу системы A и матрицу-столбец правых частей B.

Шаг 3. Формируем расширенную матрицу системы.

Шаг 4. Приводим расширенную матрицу системы к ступенчатому виду.

Шаг 5. Формируем столбец решения системы.

Шаг 6. Проверяем правильность решения.

Результаты решения приведены на рисунке 4.

1.5.6 Решение слау по формулам Крамера в MathCad

Рисунок 5 – Решение СЛАУ (Крамер)

Шаг 1. Вводим матрицу системы A и столбец правых частей B.

Шаг 2. Вычисляем определитель матрицы системы ∆. Система имеет единственное решение, если определитель, отличен от нуля.

Шаг 3. Вычисляем определители матриц, полученных заменой соответствующего столбца столбцом правых частей.

Шаг 4. Находим решение по формулам Крамера.

Результаты решения СЛАУ по формулам Крамера приведены на рисунке 5.

1.5.7 Решение слау методом «Обратной Матрицы» ( MathCad)

Шаг 1. Вводим матрицу системы A и матрицу-столбец правых частей B.

Шаг 2. Вычисляем решение системы по формуле X:=A^-1*B.

Шаг 3. Проверяем правильность решения умножением матрицы системы на вектор-столбец решения.

Результаты решения СЛАУ методом «Обратной матрицы» - рисунок 6.

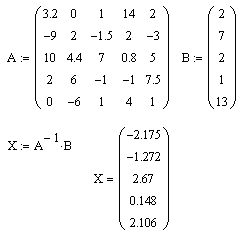
Рисунок 6 – Решение СЛАУ (Обратная матрица)

1.6 Выводы (методические указания)

Чтобы провести анализ результатов решения СЛАУ различными подходами и методами рекомендуется составить таблицу (таблица 3).

Сравнив результаты решения, следует сделать ввод о положительных и отрицательных качественных характеристиках методов, используемых в курсовой работе для решения СЛАУ (предоставляется студенту).

Таблица 3 – Результаты решения СЛАУ

М етод Значения	MS Excel	Ручной расчет	MathCAD
X1	-2,17459	-2,175	-2,175
X2	-1,27173	-1,272	-1,272
X3	2,670133	2,67	2,67
X4	0,148269	0,148	0,148
X5	2,106397	2,106	2,106