3.4 Практические рекомендации

3.4.1 Решение уравнения в ms Excel

Принимая во внимание значения исходных данных (таблица 5), запишем исследуемое уравнение (вариант ПР):

2*х³-7*х²+8*х-2=0. (27)

В MS Excel задачу будем решать методом подбора параметра, придерживаясь следующей последовательности операций:

Шаг 1. Ввести в ячейки A2:D2 значения коэффициентов уравнения (a, b, c, d)

Шаг 2. Ввести в ячейку A4 начальное (приближенное значение корня для локализации действительных корней).

Шаг 3. В ячейку A5 ввести следующее значение переменной x с учетом шага дискретности.

Шаг 4. Выделить диапазон ячеек A4:A5, и протянуть до получения приблизительно 20 значений x.

Шаг 5. Ввести в ячейку B4 формулу вычисления кубического полинома

=$A$2*A4^3+$B$2*A4^2+$C$2*A4+$D$2

Шаг 6. Протянуть формулу на весь диапазон изменения аргумента x.

Шаг 7. Оценить по полученным значениям полинома наличие корней внутри данного диапазона (изменение знака полинома на противоположный). В общем случае действительных корней может быть 1, 2 или 3.

То есть может быть 3 ситуации:

• один действительный корень и два комплексно-сопряженных;

• три действительных корня, два из которых, по крайней мере, могут быть равны;

• три различных действительных корня.

Шаг 8. Определить приближенное значение корня: смена знака значения полинома с минуса на плюс (с плюса на минус). Для наглядности построим график функции

y=2*х³-7*х²+8*х-2. (28)

Точка пересечения графика с осью абсцисс есть не что иное, как корень уравнения (28).

Приближенное значение действительного корня можно определить и по графику.

Шаг 9. С помощью процедуры «Подбор параметра», пункта меню листа Excel, определяем действительное значение корня, предварительно настроив систему: меню «Сервис» - «Параметры» - «Вычисление» - «Итерации» - «Число итераций 500» - «Относительная погрешность 0,000001».

Шаг 10. В ячейку C5 ввести ближайшее к корню значение x.

Шаг 11. В ячейку D5 ввести формулу вычисления кубического полинома =$A$2*C5^3+$B$2*С5^2+$C$2*С5+$D$2.

Шаг 12. Вычисление уточненного значения корня: «Сервис» – «Подбор параметра» - «Установить в ячейке» [D5], «Значение» [0], «Изменяя значение ячейки» [С5].

В ячейке C5 с заданной погрешностью определится уточненное значение первого корня уравнения (28).

Примечание: если действительных корней больше, чем один, то процедура повторяется.

Если действительный корень один, то нахождение комплексных корней осуществляется методом понижения степени исходного уравнения:

(ax³+bx²+cx+d)/(x-x₁)=Ax²+Bx+C

где A, B и C определяются следующим образом:

A=a,

B=b+ax_1,

C=c+bx₁+ax₁².

Шаг 13. В ячейку A27 ввести формулу: =A2.

В ячейку B27 ввести формулу: =B2+A2*C5.

В ячейку C27 ввести формулу: =C2+B2*C5+A2*C5^2.

Шаг 14. Находим дискриминант.

Введем в ячейку D27 формулу: =B27^2-4*A27*C27.

Шаг 15. Вычислим x2, x3 (комплексно-сопряженные корни).

Введем в ячейку B30 формулу:

=МНИМ.ДЕЛ(МНИМ.СУММ(-B27;МНИМ.КОРЕНЬ(D27));(2*A27))

Введем в ячейку B31 формулу:

=МНИМ.ДЕЛ(МНИМ.РАЗН(-B27;МНИМ.КОРЕНЬ(D27));(2*A27)).

Проверка решения.

Введем в ячейку B33 формулу:

=$A$2*B29^3+$B$2*B29^2+$C$2*B29+$D$2.

Введем в ячейку B34 формулу:

=МНИМ.СУММ(МНИМ.ПРОИЗВЕД(A2;МНИМ.СТЕПЕНЬ(B30;3));МНИМ.ПРОИЗВЕД(B2;МНИМ.СТЕПЕНЬ(B30;2));МНИМ.ПРОИЗВЕД(C2;B30);D2).

Введем в ячейку B35 формулу:

=МНИМ.СУММ(МНИМ.ПРОИЗВЕД(A2;МНИМ.СТЕПЕНЬ(B31;3));МНИМ.ПРОИЗВЕД(B2;МНИМ.СТЕПЕНЬ(B31;2));МНИМ.ПРОИЗВЕД(C2;B31);D2).

Результаты пошагового алгоритма нахождения корней уравнения представлены на рисунке 16.

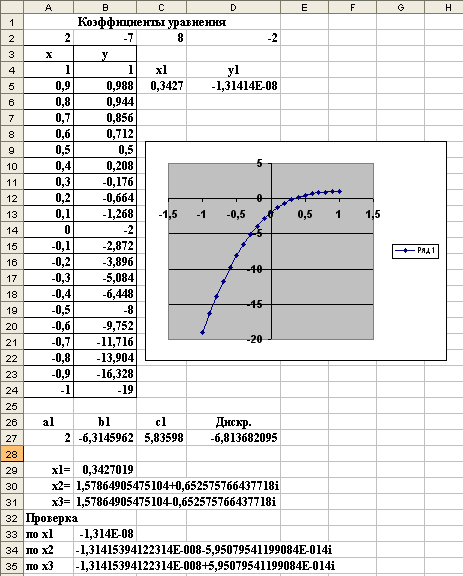
Рисунок 16 – Определение корней полинома третьей степени