3. Задача потребительского выбора.
3.1. Задача потребительского выбора или задача рационального поведения потребителя на рынке.
Задача
потребительского выбора
заключается в выборе такого потребительского
набора
,
который максимизирует его функцию
полезности при заданном бюджетном
ограничении.
Бюджетное ограничение
означает, что денежные расходы на
продукты не могут превышать денежного
дохода, то есть
,
где
–
рыночные цены одной единицы первого и
второго продуктов, соответственно, а
- доход индивидуума. Величины
-
заданы.
Формально задача потребительского выбора имеет вид:
.
Замечание. Допустимое множество представляет собой треугольник, ограниченный осями координат и бюджетной прямой. На этом множестве требуется найти точку, принадлежащую кривой безразличия с максимально возможным уровнем полезности. Графически отыскание этой точки можно описать, как переход на линии все более высокого уровня полезности до тех пор, пока эти линии имеют общие точки с допустимым множеством.
Замечание. Будем
считать, что в оптимальной точке
условия
выполняются
автоматически, вытекая из определения
функции
.
Как правило, это действительно так.
Поэтому не будем включать условие
в явном виде в
постановку задачи, что существенно
упростит ее с математической точки
зрения.
Замечание.
Рассмотрим
бюджетное ограничение
.
Если на каком-то наборе
ограничение
выполняется в виде строгого неравенства
,
то можно увеличить потребление какого-либо
из продуктов и, следовательно, увеличить
функцию полезности. Отсюда ясно, что
набор
,
максимизирующий функцию полезности,
должен обращать бюджетное ограничение
в равенство.
Исходя из сделанных выше замечаний, заменим задачу потребительского выбора на задачу на условный экстремум:
при условии
.
Если выполнены свойства 1.1.-3.1. функции полезности, то, как было показано выше, линии безразличия убывают и выпуклы вниз. Поэтому точка максимума является точкой касания линии безразличия функции полезности и бюджетной прямой.
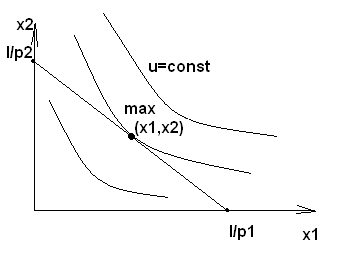
Рис. 3.1.1.
Найдем координаты точки максимума, используя метод множителей Лагранжа.
Введем функция
.
Запишем функцию Лагранжа
и исследуем ее на
безусловный экстремум. Необходимые
условия экстремума – равенство нулю
частных производных по
.
Найдем первые частные производные функции Лагранжа по и приравняем их к нулю:
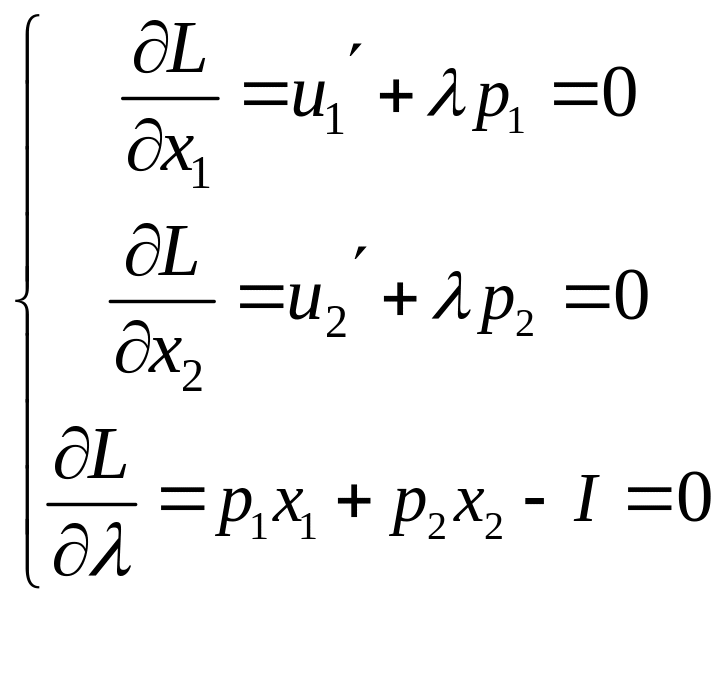
Исключив из
полученной системы трех уравнений с
тремя неизвестными переменную
,
получим систему двух уравнений с двумя
неизвестными
и
:
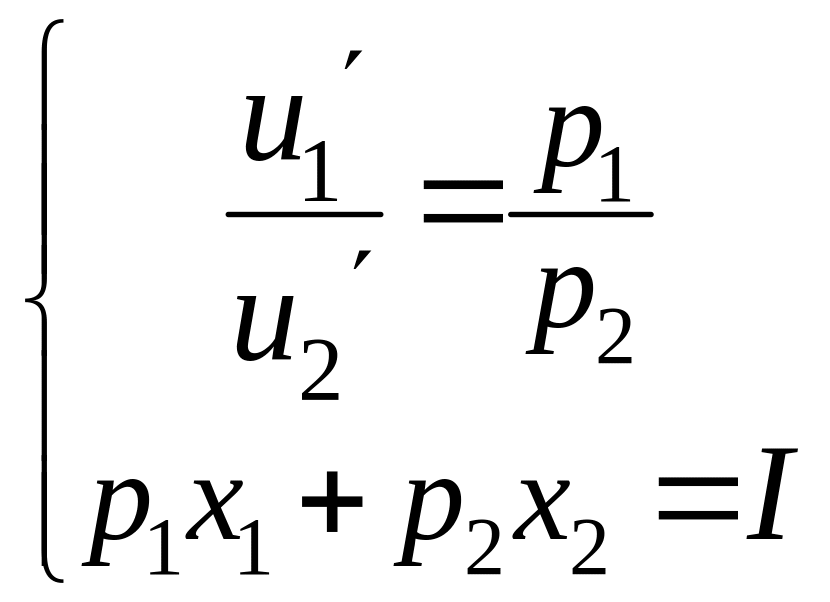
Решение этой системы есть «укороченная» критическая точка функции Лагранжа, и она же является оптимальным решением задачи потребительского выбора.
Подставив оптимальное решение в первое равенство системы, получим
,
то есть в точке локального рыночного равновесия отношение предельных полезностей продуктов равно отношению рыночных цен на эти продукты.
Отношение
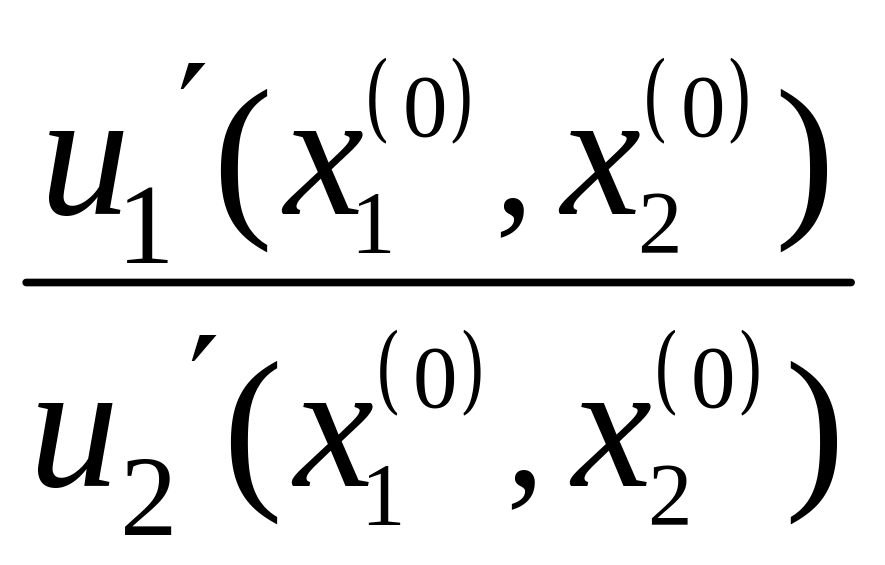равно предельной норме замещения первого
продукта вторым, поэтому в точке
локального рыночного равновесия эта
предельная норма равна отношению
рыночных цен
на продукты.
Пример.
.
Перейдем к задаче на условный экстремум:
.
Введем функцию
.
Функция Лагранжа имеет вид:
.
Найдем первые частные производные функции Лагранжа по и приравняем их к нулю:
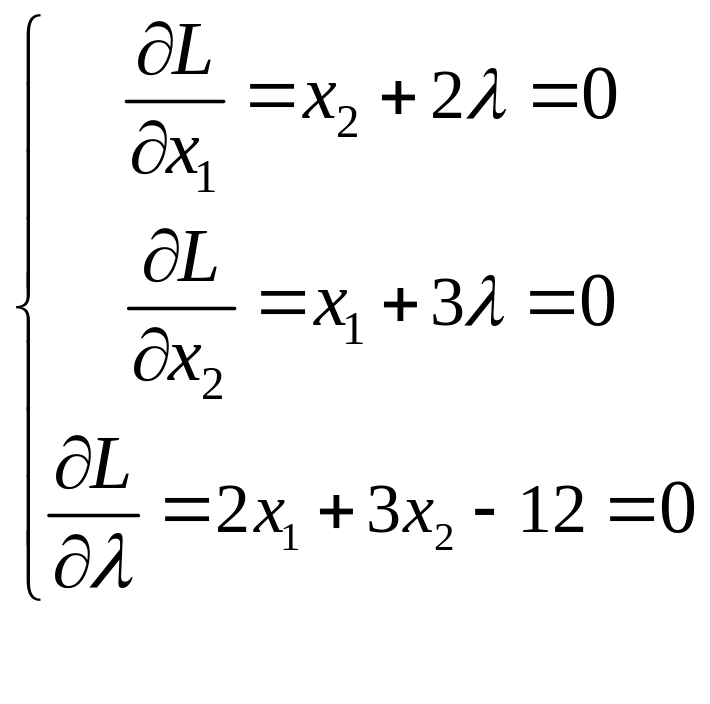
Воспользовавшись формулой
,
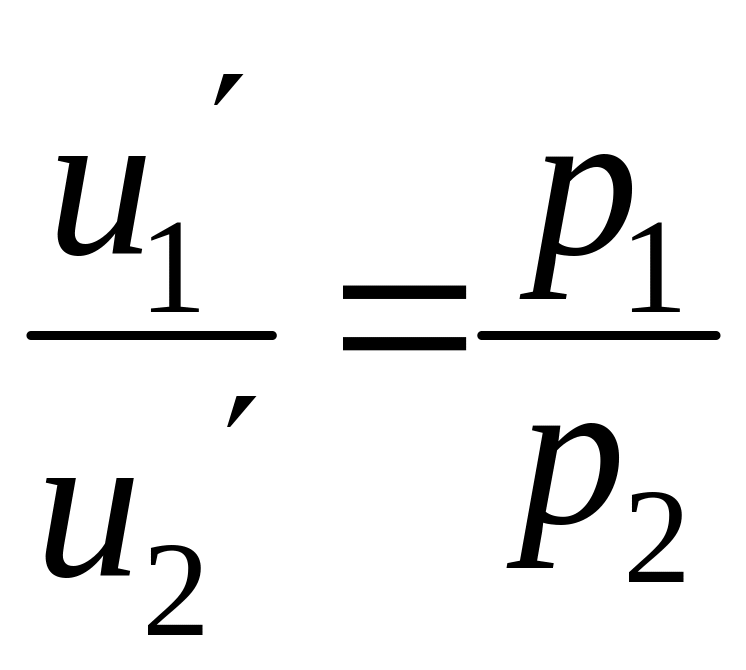получим
,
.
Подставляя полученное выражение в бюджетное ограничение
,
находим
,
,
Итак, оптимальное
решение
,
.
Замечание. Заметим, что задачу потребительского выбора можно решать и без использования метода множителей Лагранжа. Поскольку бюджетное ограничение является линейной функцией, можно выразить одну переменную через другую, подставить в функцию полезности, получить функцию полезности как функцию от одной переменной и далее искать ее экстремум.
Замечание. Решение
сохраняется при любом монотонном, то
есть сохраняющем порядок значений,
преобразовании функции полезности.
Поскольку значение
было максимальным на всем допустимом
множестве, оно остается таким же и после
монотонного преобразования функции
полезности. Таким монотонным преобразованием
может быть, например, умножение функции
на некоторое положительное число,
возведение ее в положительную степень,
логарифмирование по основанию, большему
единицы.
Замечание. Свойство 1. должно присутствовать у любой функции полезности, свойства 2. и 3. могут при монотонных преобразованиях теряться или приобретаться.
Замечание. Решение задачи потребительского выбора не изменится, если все цены и доход умножаются на некоторое положительное число. Понятно, что при этом новое бюджетное неравенство эквивалентно исходному.