2. Функция полезности.
2.1. Определение функции полезности.
Рассмотрим потребительские наборы из двух благ (x1,x2), где x1 – количество единиц первого блага, x2 - количество единиц второго блага.
Выбор потребителя характеризуется отношением предпочтения: считается, что потребитель про каждые два набора можно сказать, либо один из них более желателен, чем другой, либо он не видит между ними разницы. Отношение предпочтения транзитивно, то есть если набор А(a1,a2) предпочтительнее набора В(b1,b2), а набор В предпочтительнее набора С(c1,c2), то набор А предпочтительнее набора С.
На множестве потребительских наборов (x1,x2) определена функция u(x1,x2), называемая функцией полезности потребителя. Значение u(x1,x2) равно потребительской оценке индивидуума для набора (x1,x2). Потребительскую оценку u(x1,x2) набора (x1,x2) принято называть уровнем (степенью) удовлетворения потребностей индивидуума, если он потребляет данный набор (x1,x2).
Каждый потребитель, вообще говоря, имеет свою функцию полезности. Однако, для всех потребителей верно то, что если набор А предпочтительнее набора В, то u(A)>u(B).
2.2. Свойства функции полезности.
Обычно рассматриваются функции полезности, удовлетворяющие следующим свойствам:
Свойство 1. Возрастание потребления одного продукта при постоянном потреблении другого продукта ведет к росту потребительской оценки, то есть
если
,
то
,
если
,
то
.
Свойство 1.1.
Пусть для всех
выполнено
,
.
Замечание. Из свойства 1.1. следует свойство 1.
Определение.
Первые частные
производные функции полезности называются
предельными полезностями продуктов:
– предельная полезность первого
продукта,
- предельная
полезность второго продукта.
Свойство 2. Предельная полезность каждого продукта уменьшается, если объем его потребления растет. Это свойство называется законом убывания предельной полезности.
Свойство 2.1. Пусть для всех выполнено
,
.
Замечание. Из свойства 2.1. следует свойство 2.
Свойство 3. Предельная полезность каждого продукта увеличивается, если растет количество другого продукта, то есть продукт, количество которого фиксировано, оказывается относительно дефицитным.
Свойство 3.1. Пусть для всех выполнено
.
Замечание. Из свойства 3.1. следует свойство 3.
Замечание. Предположение 3. (свойство 3.1.) вводится не всегда. Если блага могут полностью замещать друг друга, то свойство 3. не выполняется.
Определение.
Линия, соединяющая потребительские
наборы, имеющие один и тот же уровень
удовлетворения потребностей индивидуума,
называется линией безразличия, то есть
линия безразличия – это линия уровня
функции полезности
.
Определение. Множество линий безразличия называется картой линий безразличия.
Замечание. Условия 1.1.-3.1. означают, что линии безразличия убывают и выпуклы вниз.
Действительно,
рассмотрим уравнение кривой безразличия
.
Если u
имеет всюду непрерывные производные
второго порядка и выполнено свойство
1.1., то в окрестности любой точки кривой
безразличия это равенство задает неявно
дважды дифференцируемую функцию
.
По правилу дифференцирования неявной
функции имеем:
.
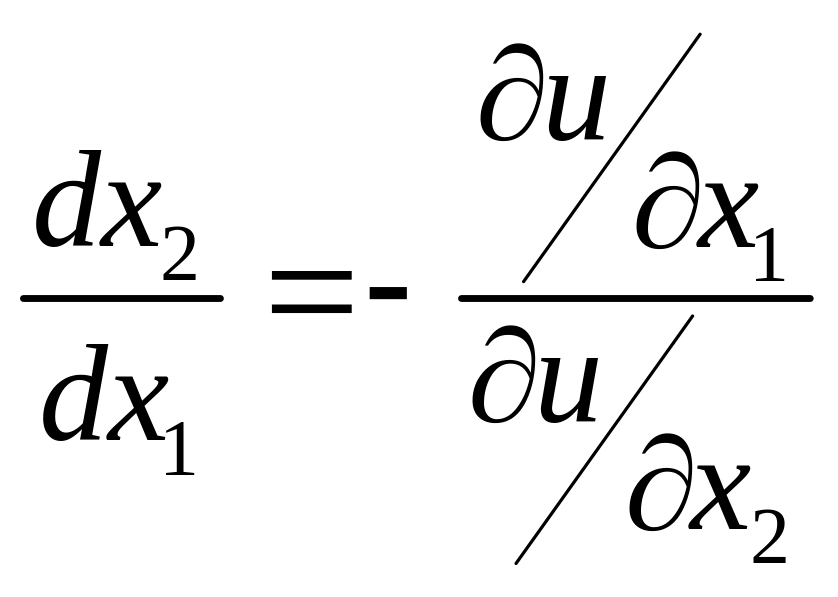По свойству 1.1. , . Поэтому
.
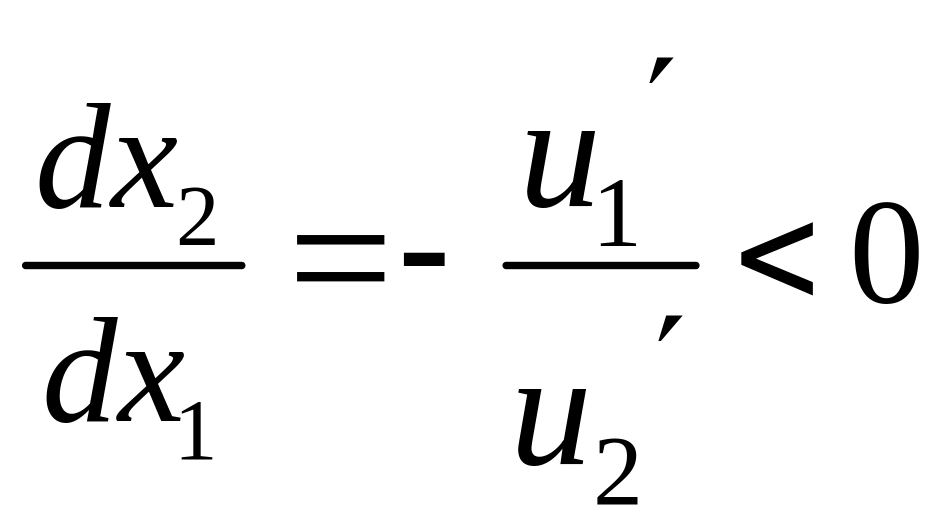Следовательно, функция является убывающей, так как ее производная отрицательна.
Найдем вторую производную функции . Используя условия 1.1.-3.1., получим
.
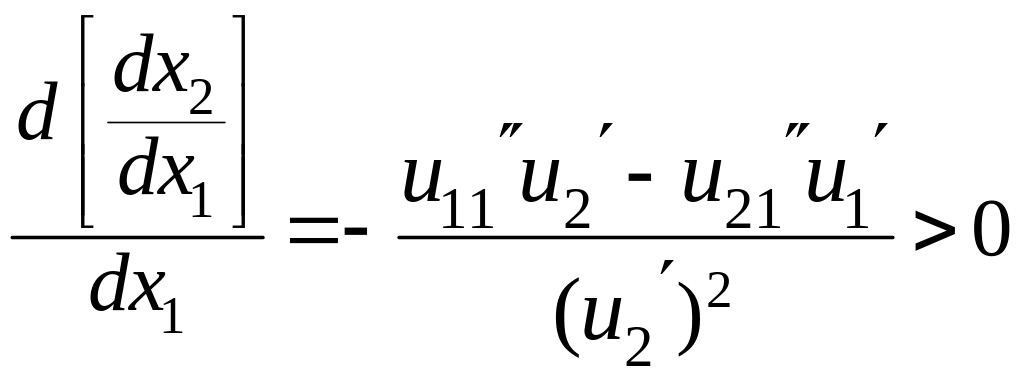Это означает, что функция выпукла вниз.
Итак, из свойств 1.1.- 3.1. следует, что линии безразличия убывают и выпуклы вниз.
Пример.
Пусть функция полезности имеет следующий вид:
,где
Свойства 1.1. и 2.1. выполняются, свойство 3.1. не выполняется:
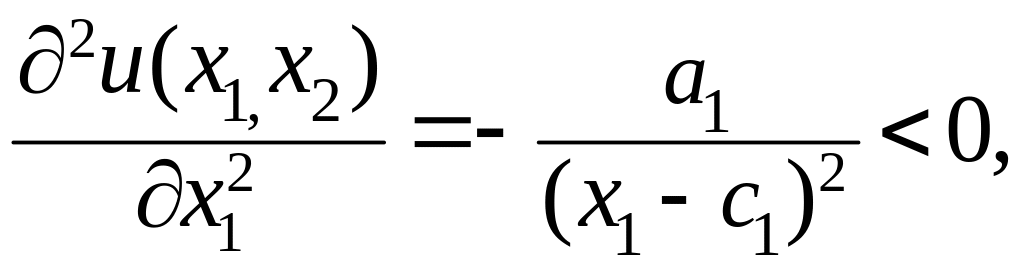
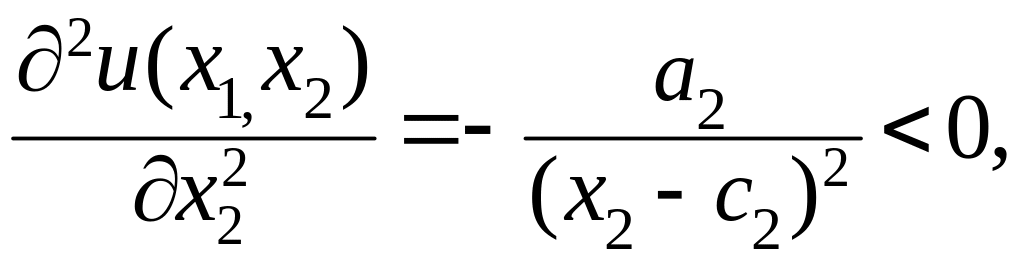
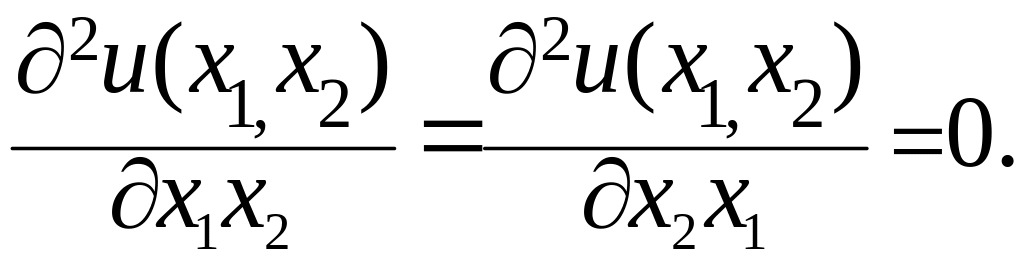
Замечание.
Линии безразличия, соответствующие
разным уровням удовлетворения
потребностей, не касаются и не пересекаются.
Если C1<C2<C3,
то
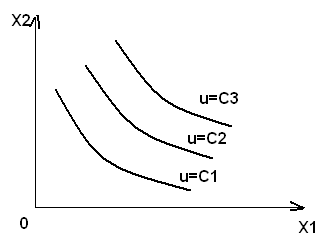
Рис. 2.2.1.