
- •1. Эластичность функции.
- •1.3. Свойства эластичности.
- •1.4. Эластичность некоторых функций.
- •1.5. Применение эластичности в экономическом анализе.
- •2. Функция полезности.
- •2.1. Определение функции полезности.
- •2.2. Свойства функции полезности.
- •3. Задача потребительского выбора.
- •3.1. Задача потребительского выбора или задача рационального поведения потребителя на рынке.
- •3.3. Общая модель задачи потребительского выбора.
1. Эластичность функции.
1.1. Определение эластичности функции.
Определение. Эластичностью функции y=f(x) называется предел отношения относительных изменений переменных y и x, то есть
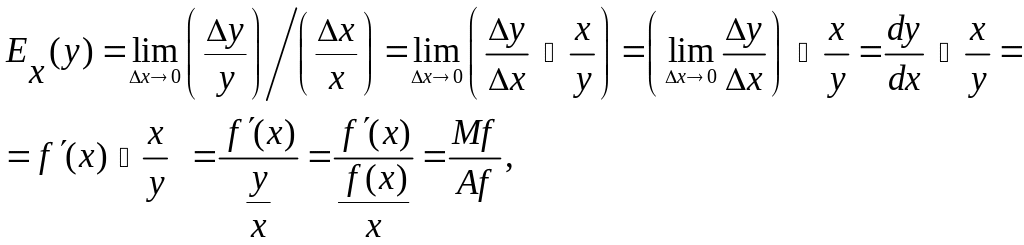
где Mf - маржинальное значение функции f в точке x,
Af – среднее значение функции f в точке x.
Замечание. Эластичность функции показывает приближенно, на сколько процентов изменится функция y=f(x) при изменении независимой переменной x на 1%.
Замечание. Эластичность может быть представлена в виде логарифмической производной
![]() ,
так как
,
так как
![]() и
и
![]() .
.
Замечание.
Производная
функции y=f(x)
также является одним из показателей
реагирования одной переменной на
изменение другой.
![]() характеризует
скорость изменения функции с изменением
аргумента. Однако, в экономических
исследованиях такая характеристика
не очень удобна, поскольку зависит от
единицы измерения. Например, если
рассмотреть функцию спроса Q
на картофель в зависимости от его цены
р,
то значение производной зависит от
того, измеряется ли спрос в килограммах
или в центнерах. Поэтому было введено
понятие эластичности, чтобы изучать
связь не абсолютных изменений функции
и аргумента, а связь их относительных
или процентных изменений.
характеризует
скорость изменения функции с изменением
аргумента. Однако, в экономических
исследованиях такая характеристика
не очень удобна, поскольку зависит от
единицы измерения. Например, если
рассмотреть функцию спроса Q
на картофель в зависимости от его цены
р,
то значение производной зависит от
того, измеряется ли спрос в килограммах
или в центнерах. Поэтому было введено
понятие эластичности, чтобы изучать
связь не абсолютных изменений функции
и аргумента, а связь их относительных
или процентных изменений.
Замечание. Производная функции выражает предельные издержки производства и характеризует приближенно дополнительные затраты на производство единицы дополнительной продукции.
1.2. Геометрическая интерпретация эластичности.
Рассмотрим убывающую вогнутую функцию, представленную на рисунке 1.2.1. Найдем эластичность этой функции в произвольной точке С(x,y). Для этого проведем касательную АВ в точке С к графику функции y=f(x).
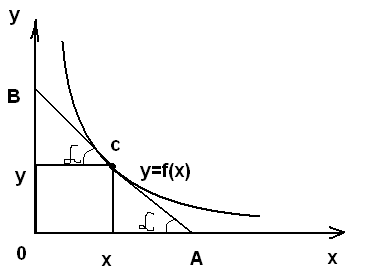
рис. 1.2.1.
Утверждение.
![]() ,
то есть геометрически эластичность
убывающей выпуклой вниз функции равна
отношению расстояний по касательной
от точки С(x,y)
до точек пересечения касательной с
осями OY
и OX,
взятому со знаком минус.
,
то есть геометрически эластичность
убывающей выпуклой вниз функции равна
отношению расстояний по касательной
от точки С(x,y)
до точек пересечения касательной с
осями OY
и OX,
взятому со знаком минус.
Действительно,
из треугольника ACX
следует, что
![]() .
Так как производная функции y=f(x)
в точке С
равна
.
Так как производная функции y=f(x)
в точке С
равна
![]() ,
,
![]() то
то
![]() ,
кроме того
,
кроме того
![]() ,
и следовательно
,
и следовательно
![]() .
Треугольники CBY
и CAX
подобны,
поэтому
.
Треугольники CBY
и CAX
подобны,
поэтому
![]() ,
кроме того
,
кроме того
![]() ,
следовательно
,
следовательно
![]() .
Итак
.
.
Итак
.
Замечание.
В случае выпуклой возрастающей функции
эластичность по абсолютной величине
также равна отношению
![]() .
В общем случае знак эластичности для
возрастающей или убывающей выпуклой
функции будет определяться следующим
образом. Если точки А
и В
лежат по одну сторону от точки С
на касательной, то надо выбрать знак
«+» (рис. 1.2.2., рис. 1.2.3.), если же по разные
стороны от точки С,
то знак минус (рис. 1.2.1.).
.
В общем случае знак эластичности для
возрастающей или убывающей выпуклой
функции будет определяться следующим
образом. Если точки А
и В
лежат по одну сторону от точки С
на касательной, то надо выбрать знак
«+» (рис. 1.2.2., рис. 1.2.3.), если же по разные
стороны от точки С,
то знак минус (рис. 1.2.1.).

Рис. 1.2.2.
![]() ,
так как
,
так как
![]() .
.
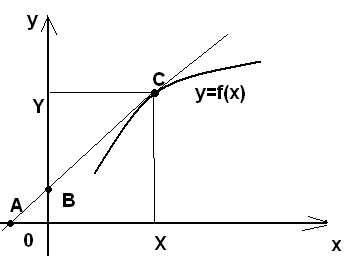
Рис. 1.2.3.
![]() ,
так как
,
так как
![]() .
.
1.3. Свойства эластичности.
1. Эластичность – безразмерная величина, то есть ее значение не зависит от того, в каких единицах измерены величины:

Действительно,

2. Эластичность взаимообратных функций – взаимообратные величины:
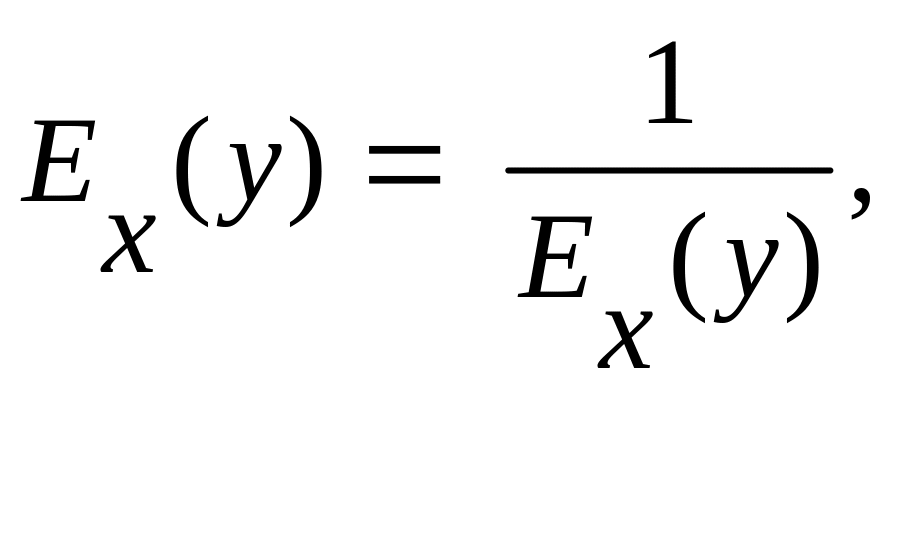
Действительно,
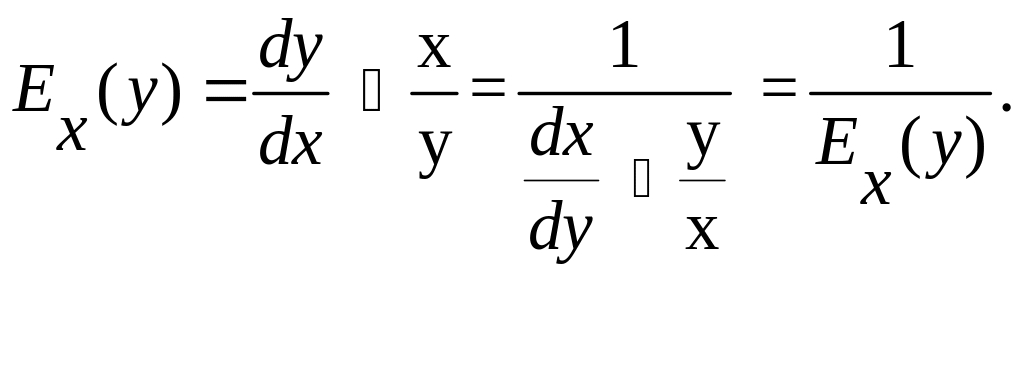
Замечание. Эластичность спроса по цене обратна эластичности цены р по величине спроса Q
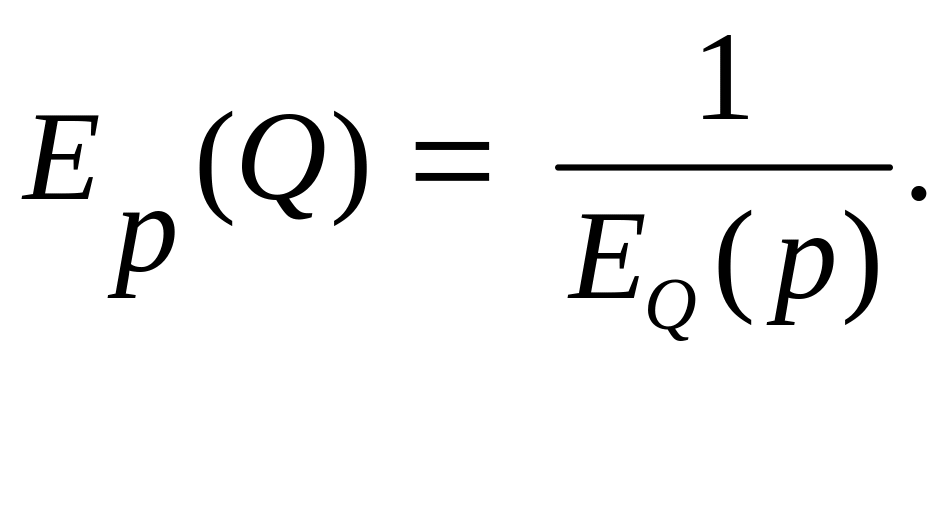
3. Эластичность произведения двух функций f(x) и g(x), зависящих от одного и того же аргумента x равна сумме эластичностей:
![]()
Действительно,
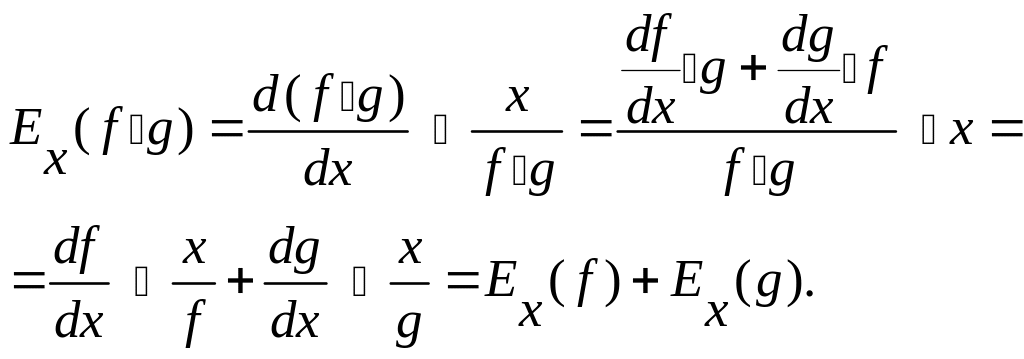
4. Эластичность частного двух функций f и g и от того же аргумента равна разности эластичностей:
![]()
Действительно,

5. Эластичность суммы двух функций f и g от одного и того же аргумента может быть найдена по следующей формуле:
![]()
Действительно,
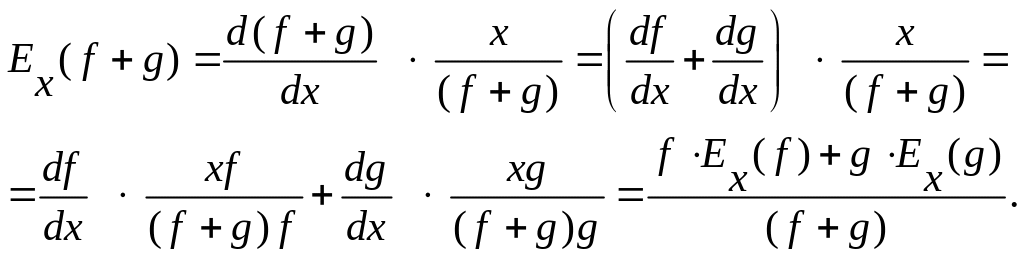
6. Эластичность
функции равна произведению независимой
переменной x
на темп изменения функции y:
![]() ,
то есть
,
то есть
![]() .
.
