
- •Колледж телекоммуникаций
- •Основные определения
- •Сигналы электросвязи и их спектры
- •Способы представления сигналов
- •Для периодического прямоугольного сигнала (рис. 6) математическая модель:
- •Виды телекоммуникаций (виды электросвязи)
- •Классификация линий связи (лс)
- •Многоканальные системы передачи
- •Модуляция и детектирование
- •Амплитудная модуляция
- •Сигнала а), и модулированного сигнала б).
- •Однополосная амплитудная модуляция
- •Контрольные вопросы
- •Частотная модуляция
- •Математическая модель частотно – модулированного (чм) сигнала
- •Спектральные диаграммы
- •Ширина спектра чм-сигнала
- •Контрольные вопросы
- •Контрольные вопросы
- •Детектирование (демодуляция)
- •Генерирование колебаний.
- •Контрольные вопросы
- •Автогенераторы типа lc
- •Контрольные вопросы
- •Автогенераторы типа rc
- •Автогенераторы типа rc с фазосдвигающими цепочками
- •Контрольные вопросы
- •Электрические фильтры
- •Контрольные вопросы и задания
- •Как у всякого четырехполюсника, характеристическое сопротивление фильтра
- •Фильтры верхних частот фвч
- •Полосовые фильтры
- •Заграждающие фильтры
- •Фильтры типа «к» и типа «m»
- •Контрольные вопросы
- •Контрольные вопросы
- •НелинейнЫе цепи, их характеристики и свойства Классификация электрических цепей
- •Свойства нелинейных электрических цепей
- •Аппроксимация характеристик нелинейных элементов
- •Методы анализа отклика нелинейных цепей
- •Вопросы и задания
Контрольные вопросы
1.Дать определение частотной модуляции
2.Дать определение девиации частоты.
3.От чего зависит девиация частоты при ЧМ?
4. Построить спектральную диаграмму ЧМ сигнала, если fнес= 900 кГц; Fc = 3 кГц; индекс модуляции М = 4. Определить девиацию частоты. Определить ширину спектра.
Фазовая модуляция (ФМ)
1. Математическая модель
При фазовой модуляции фаза несущего колебания изменяется по закону модулирующего u(t). Приращение фазы несущего колебания можно записать ΔΨ(t)=aU(t), где а - коэффициент пропорциональности. Фаза ФМ колебания: Ψ(t)= ωot+Ψ+ aU(t).
Общая математическая модель ФМ сигнала: SФМ(t)=Umsin[ωot+Ψ+ aU(t)]
Если модулирующий сигнал гармонический U(t)=UmsinΩt, то
SФМ(t)=Umsin(ωot+аUmsinΩt+Ψ)
ΔΨm=аUm – наибольшее отклонение фазы называется индексом фазовой модуляции.
Частота
ФМ сигнала ω(t)=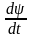 =
ωo+аUm
ΩcosΩt=
ωo+Δωm
cosΩt
=
ωo+аUm
ΩcosΩt=
ωo+Δωm
cosΩt
Δωm= аUmΩ – девиация частоты.
2. Временные диаграммы.
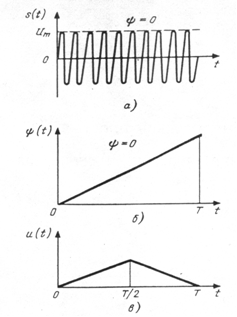
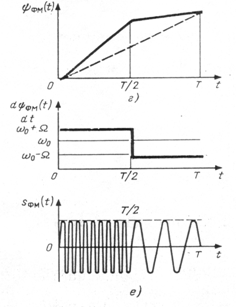
Рис. 18. Временные диаграммы
а) Гармонический сигнал несущей частоты.
б) Изменение фазы несущего колебания во времени
в) Модулирующий (первичный) сигнал.
г) Изменение фазы модулированного сигнала
д) Изменение частоты во времени при ФМ, пропорциональное дифференциалу изменения фазы, т.е. дифференциалу изменения модулирующего сигнала.
е) Фазо-модулированный сигнал.
3. Сравнение спектров ЧМ и ФМ сигналов
Сравнивая сигналы с ФМ и ЧМ можно обнаружить, что частота обоих сигналов изменяется по гармоническому закону, а девиация частоты оказывается разной: при частотной модуляции Δωm= аUm, при фазовой Δωm= аUmΩ, т. е. для ЧМ сигнала девиация частоты не зависит от частоты модулирующего сигнала Ω, для ФМ - зависит. Структура спектра ФМ сигнала такая же, как у ЧМ сигнала. Ширина спектра определяется по формуле
Δω =2(ΔΨm +1)Ω.
Ширина спектра зависит от частоты модулирующего сигнала.
Контрольные вопросы
Дать определение фазовой модуляции
От чего зависит девиация частоты при ФМ?
От чего зависит индекс модуляции при ФМ?
От чего зависит ширина спектра при ФМ?
Как связаны изменения фазы и изменения частоты при ФМ?
Детектирование (демодуляция)
Принцип детектирования – процесс выделения модулирующего сигнала из модулированного колебания. Он является обратным процессу модуляции, поэтому называется демодуляцией.
На входе амплитудного детектора в спектре АМ сигнала присутствуют частоты ωo,
(ωo + Ω) и (ωo – Ω), а на выходе должен быть передаваемый сигнал с частотой Ω. Следовательно, амплитудный детектор должен содержать нелинейную цепь (диод - VD) для создания новых спектральных составляющих, среди которых должна быть составляющая с низкой частотой Ω, выделяемая затем с помощью фильтра RC.
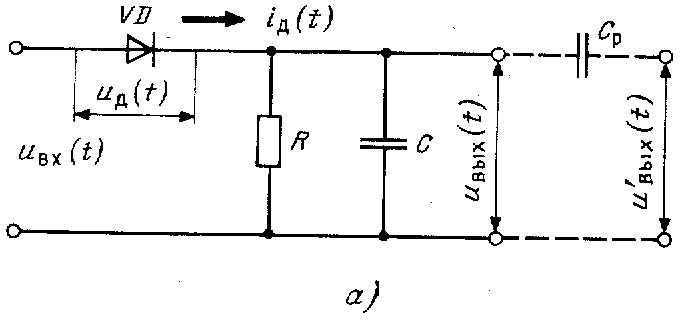
Рис.19 Схема простейшего амплитудного детектора на диоде
Диод обладает односторонней проводимостью, поэтому пропускает только положительные полупериоды входного сигнала. В отрицательные полупериоды диод закрыт. Спектр такого однополупериодного сигнала с изменяющейся амплитудой содержит и НЧ и ВЧ гармоники.
Элементы
ФНЧ RC
подбираются так, чтобы для ВЧ гармоник
конденсатор представлял очень малое
сопротивление
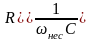 ; для НЧ гармоник
– очень большое сопротивление
; для НЧ гармоник
– очень большое сопротивление
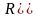 .
.
Тогда НЧ гармоники создают падение напряжения на выходе Uвых = UНЧ, пропорциональное огибающей АМ сигнала.
