Свойства определителей
Перечислим некоторые свойства полезные при оперировании с определителями.
Если все элементы некоторой строки (или столбца) равны 0, то и определитель равен 0.
Это непосредственно следует из определения, т.к., в этом случае, каждое слагаемое выражения (2) содержит равный нулю множитель.
Общий множитель элементов строки (или столбца) можно вынести за знак определителя.
Также следует из определения (2).
Если в определителе переставить между собой две строки (или столбца), то значение определителя изменится на противоположное.
Перестановка строк влечёт перестановку номеров и изменение числа инверсий на нечётную величину.
Если в определителе две строки (или столбца) пропорциональны, то он равен нулю.
Действительно, согласно свойству (2), вынося коэффициент пропорциональности, получим определитель, имеющий две равные строки (или столбца). И переставив их, далее, получим
- ,
откуда
0.
Если в определителе каждый элемент строки (или столбца) представим в виде суммы двух слагаемых, то такой определитель равен сумме двух определителей, в первом из которых в качестве элементов данной строки используются первые слагаемые, во втором, - вторые.
В этом случае, выражение (2) можно представить в виде суммы двух выражений и, следовательно, определителей.
Определитель не изменяется, если к строке (или столбцу) прибавить линейную комбинацию других строк (или столбцов).
По свойству 4,5, такая процедура эквивалентна прибавлению к исходному определителю линейной комбинации определителей с равными строками (или столбцами).
Сумма произведений элементов какой-либо строки (или столбца) на алгебраические дополнения элементов другой строки (или столбца) равна 0.
Действительно, такое выражение эквивалентно определителю, имеющего равные строки (или столбы).
Значение определителя не изменится, если все соответствующие строки и все столбцы поменять местами.
Действительно, для выполнения указанной процедуры на первом этапе необходимо вторую строку переставить с первой, третью – с первыми двумя и т.д., наконец, последнюю ,- с (n – 1) предыдущими. Это требует n(n-1)/2 перестановок строк и такого же числа изменений знака. На втором этапе, проводя аналогичную перестановку столбцов, знак определителя поменяется ещё n(n – 1)/2 раз и в итоге совпадает с исходным.
Замечание. Использование перечисленных свойств позволяет упрощать и снижать трудоёмкость вычисления определителей. Так, последовательно комбинируя соответствующие строки исходный определитель можно привести, например, к правотреугольному виду. Тогда ,его вычисление сводится к перемножению диагональных элементов. Эта процедура, в случае определителя 4-го порядка, требует выполнения 37 операций алгебраического сложения и умножения. Сравните эту цифру с указанными.
в Замечании 1 п. 1.
Примеры
Рассмотрим для иллюстрации несколько примеров.
Пример 1.Вычислить
.
Решение.
1. Вынесем из первого столбца общий множитель
6
.
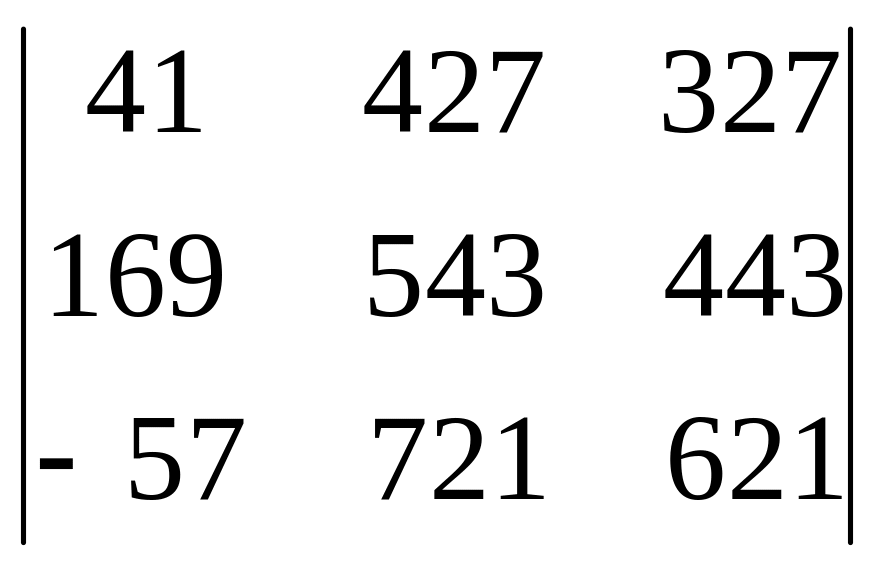2. Вычтем из второго столбца третий
6
.
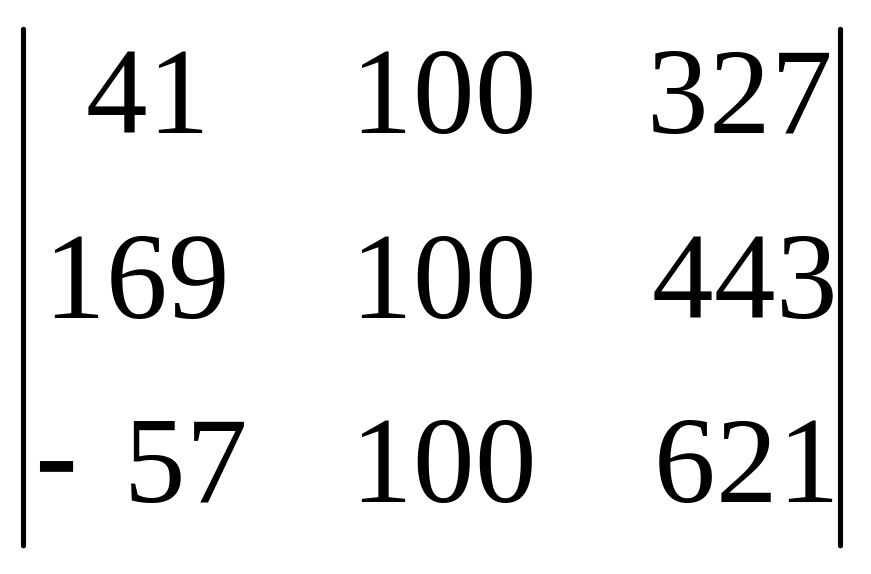3. Вынесем из второго столбца общий множитель
6
100
.
4. Вычтем из второй строки первую
600
.
5. Вынесем из второй строки общий множитель
600
4
.
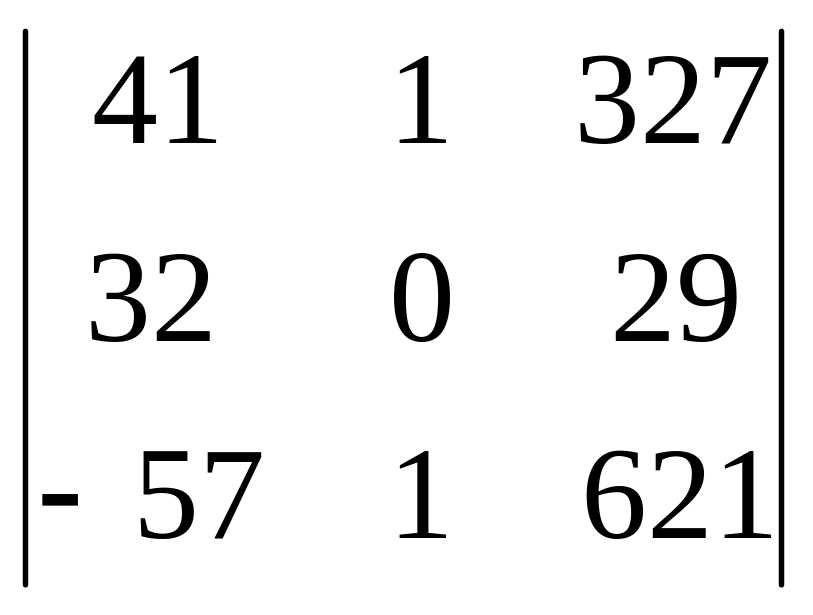6.Вычтем из первого столбца второй, умноженный на 41
2400
.
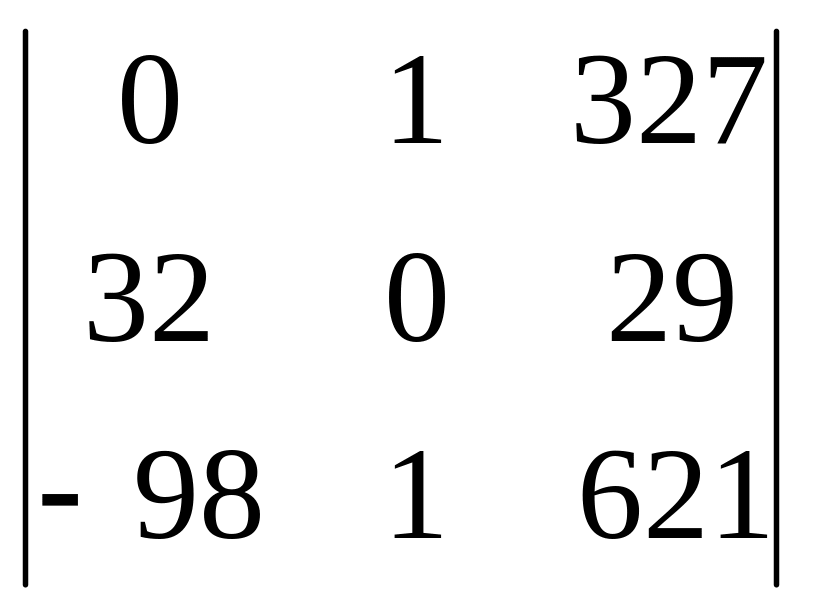7.Вынесем из первого столбца общий множитель
2400
2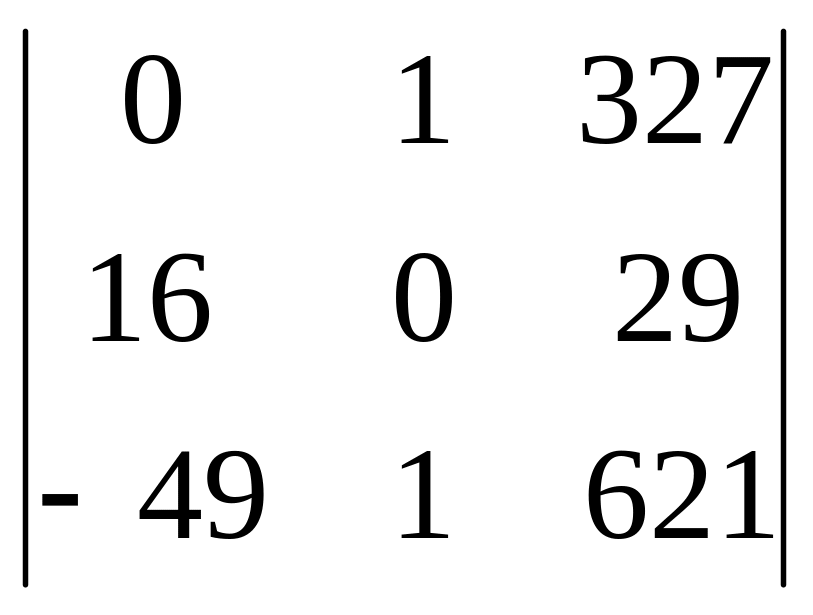
.
8. Вычтем из третьей строки первую
4800
.
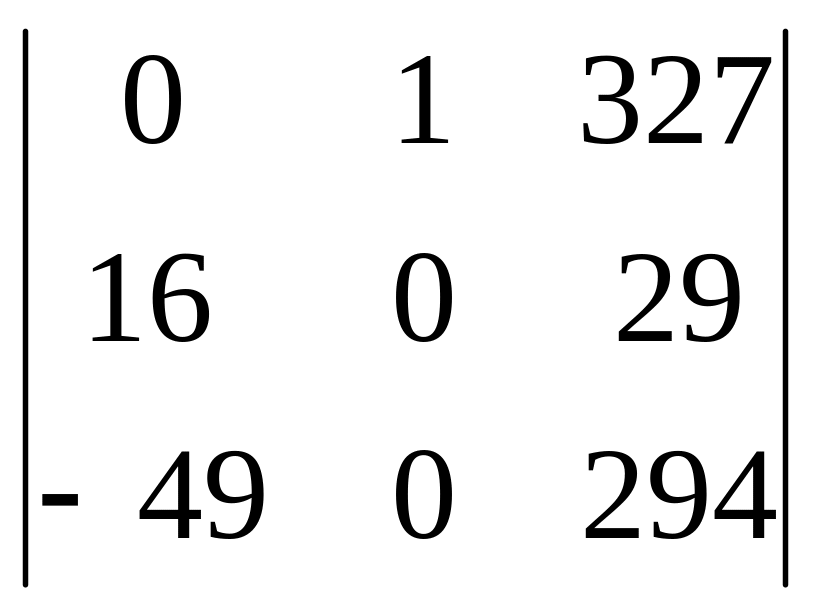9.Вынесем из третьей строки общий множитель
4800
49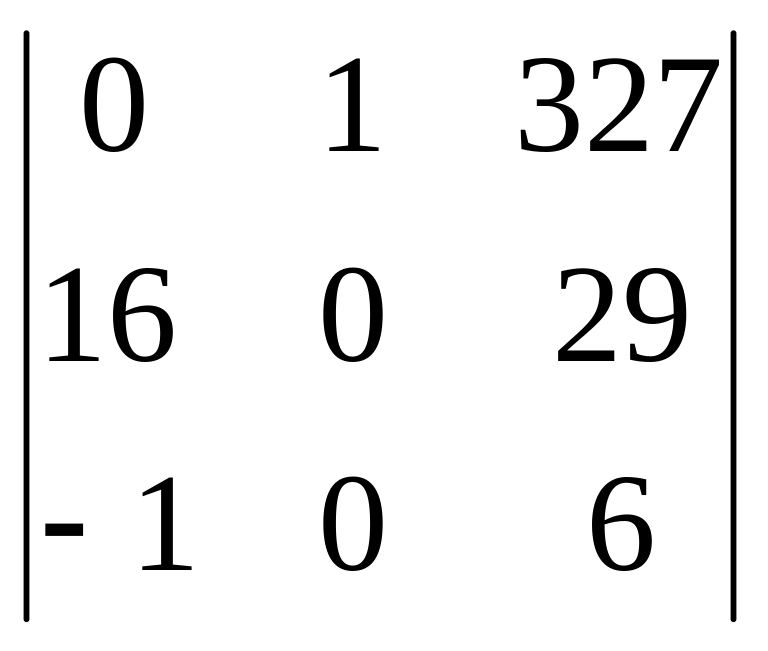
.
10. Вычтем из третьего столбца второй, умноженный на 327
4800
49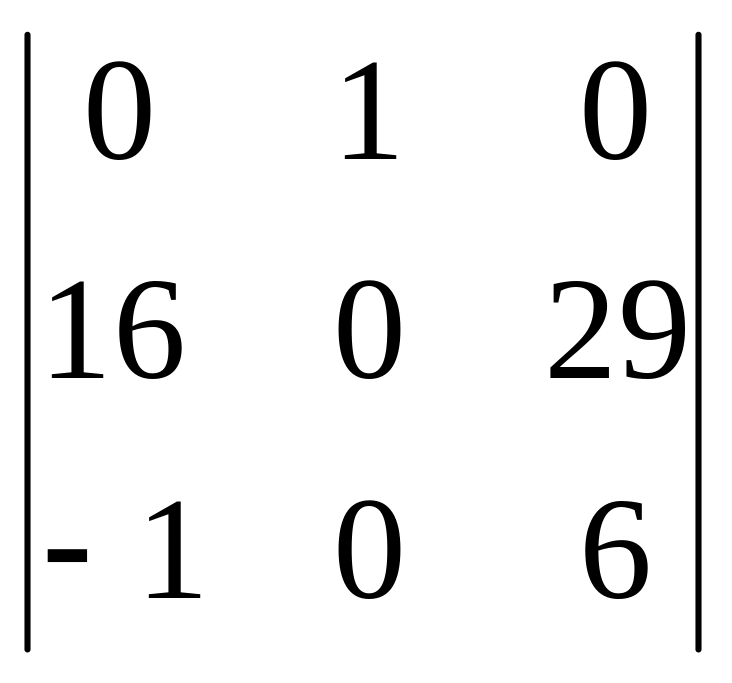
.
11.Раскрывая по первой строке
= 4800 49 (-1)(16 6+29),
получим
=
-
10
49
48
125=
-10
49
12
(4
125)=
-10
49
6=
-10
49
6=
-294
10
.
Пример 2. Числа 204, 527 и 255 делятся на 17.Доказать, что определитель
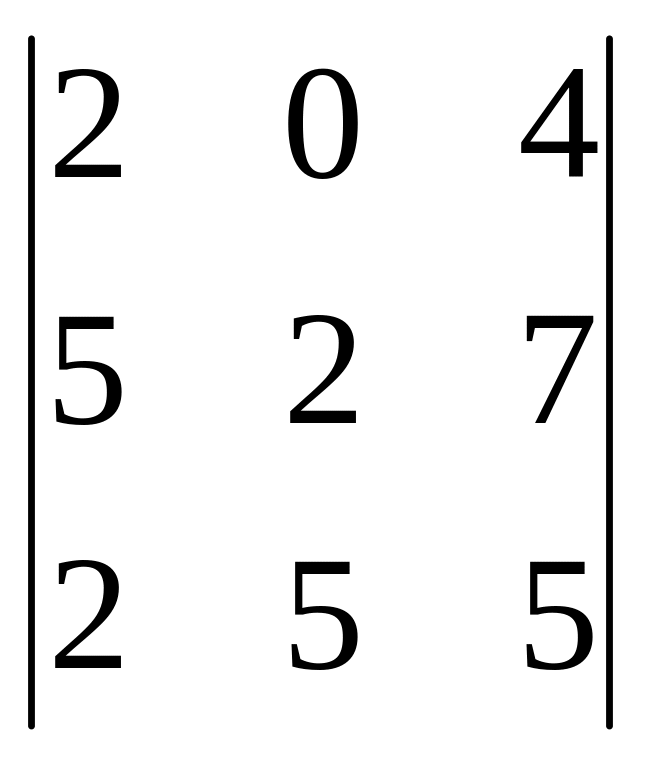
также делится на 17.
Решение. Прибавим к третьему столбцу первый столбец, умноженный на 100 и второй, - умноженный на 10. Получим
.
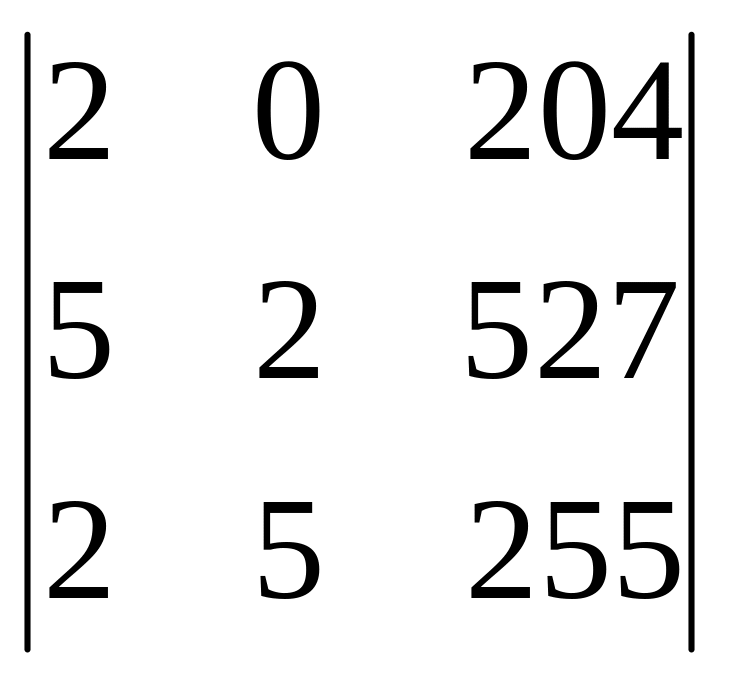Каждый элемент третьего столбца делится на 17, следовательно, делится на 17 и сам определитель.
Пример 3.Вычислить
.
Решение.1. Вычтем четвёртую строку из всех предыдущих.
.
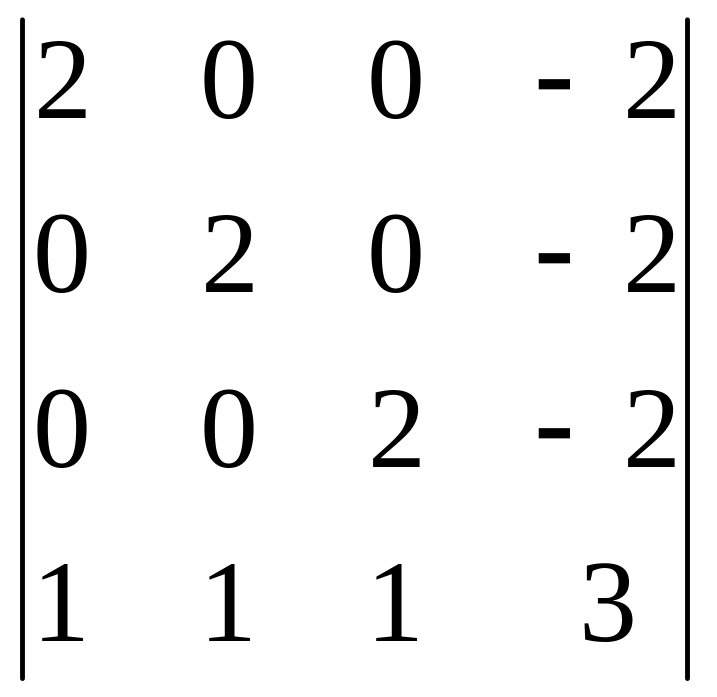2. Вынесем из первых трёх строк общие множители .
2
2
2
.
3. Вычтем первую строку из четвёртой.
8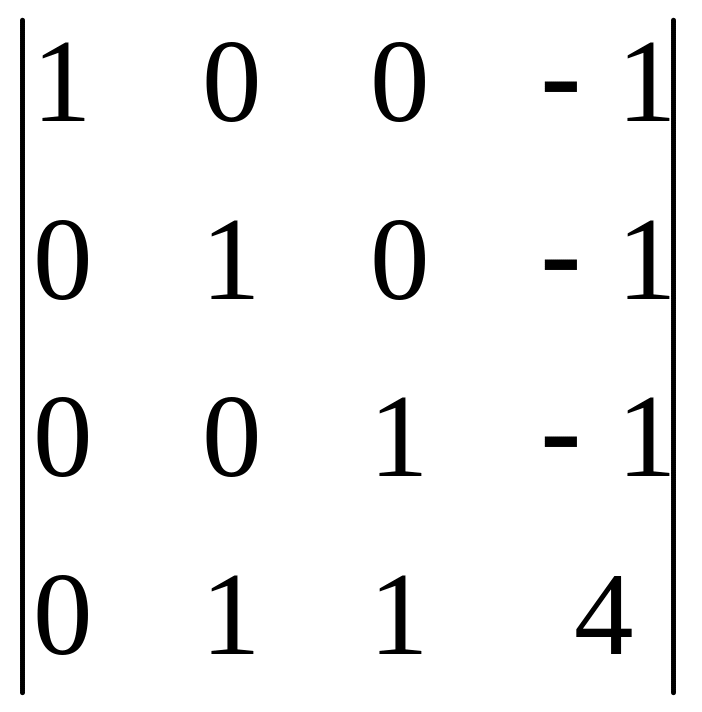
.
4. Вычтем вторую строку из четвёртой
8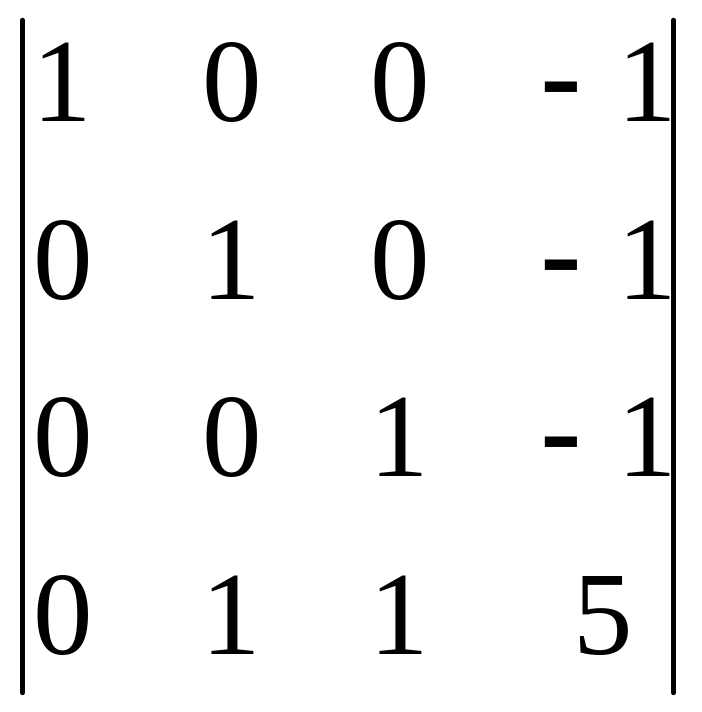
.
5. Вычтем третью строку из четвёртой
8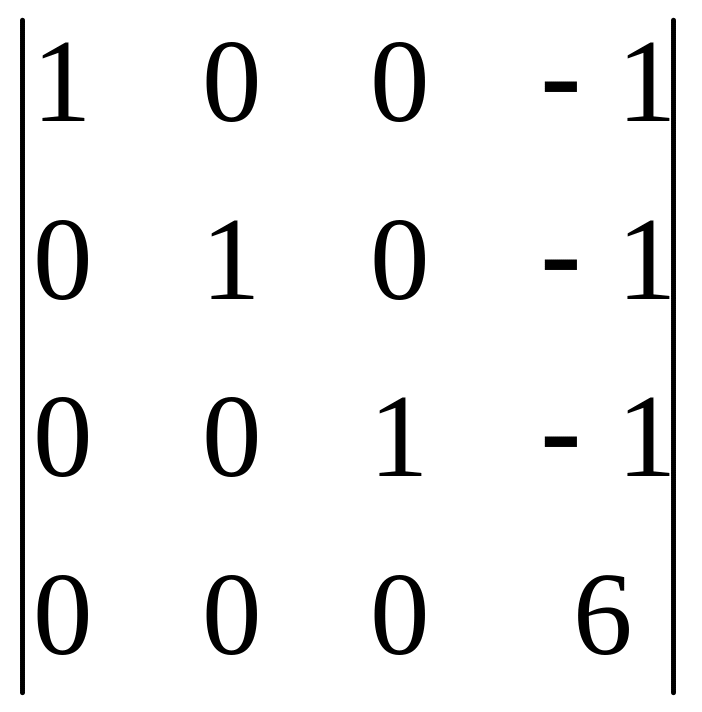
.
6. Полученный определитель равен произведению диагональных элементов, поэтому
8 6=48.