Лекция 11. Специальные кривые

Рассмотрим ниже некоторые из плоских линий, которые нередко используются при рассмотрении демонстрационных примеров в различных разделах математики, описав, предварительно полярную и параметрическую формы представления кривых.

1. Полярная и параметрическая формы представления

1.1. Полярные координаты. Рассмотрим на плоскости произвольную ось и назовём её полярной. Тогда положение произвольной точки плоскости можно определить двумя величинами, расстоянием

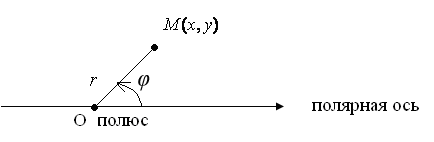
точки от полюса О, оно называется полярным радиусом, и углом , образованным отрезком ОМ с положительным направлением полярной оси. Набор ( , ) и называется полярными координатами точки . Обычно предполагается, что 0, а - < < .

В том случае, когда полярная ось совпадает с осью ох, а полюс, с началом декартовой системы координат, то справедливы

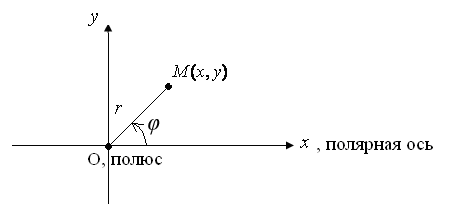
следующие соотношения :

= cos , = sin ,

или, в обратную сторону

= , tg = ,

откуда, с точностью до 2 , может быть определено, с учётом знаков и , значение полярного угла .

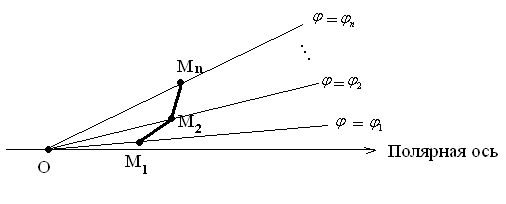
В полярной форме уравнение кривой имеет вид

= ( )

и построение графика производится следующим образом. Проводятся лучи = ,…, = , на которых откладывается точки , ,…, на расстояниях , ,…, от полюса, соответственно. Далее, соединив полученные точки отрезками или проводя через них плавную кривую, получим при малых = приближённое изображение кривой.

1.2. Параметрическая форма представления кривых. В общем случае она выглядит так :

,

где независимая переменная ,обычно ,называется параметром. Таким образом, связь между декартовыми координатами, в этом случае, задаётся косвенно, через параметр .

2. Специальные кривые

2.1.Спираль Архимеда. Спиралью Архимеда называется траектория точки, которая движется с постоянной скоростью вдоль некоторой прямой, которая, в свою очередь, вращается с постоянной угловой скоростью относительно одной из своих точек.

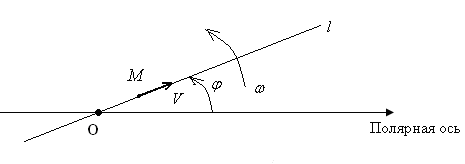
Пусть прямая l вращается вокруг полюса О и в начальный момент совпадает с полярной осью, а положение точки , с полюсом О, тогда соотношения

= , = ,

представляют собой уравнения траектории в параметрической форме, или, после исключения из них переменной , получаем зависимость

= ,

где = / , уравнение кривой в полярных координатах. График спирали Архимеда следующий

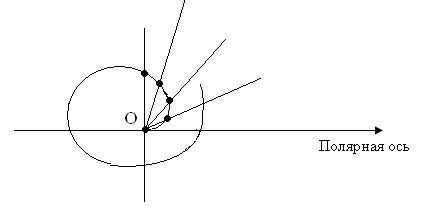
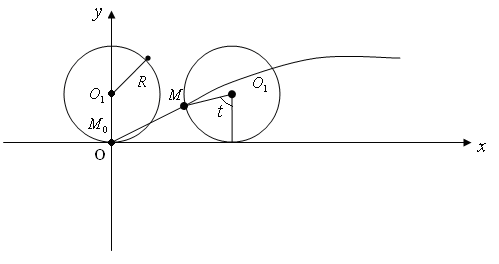
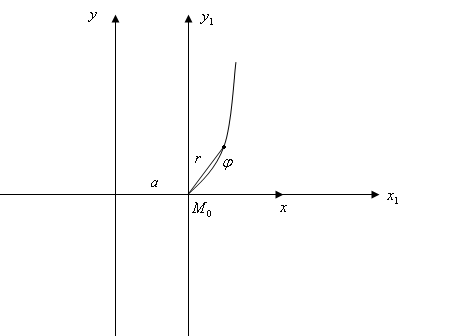
2.2. Циклоида. Циклоидой называется траектория точки, расположенной на окружности, которая катится без скольжения вдоль некоторой прямой.

Предположим, что окружность имеет радиус ( на рисунке R) и движется вдоль оси ох, причём в начальный момент положение исследуемой точки совпадает с началом координат и введём параметр указанным на рисунке образом. Учитывая ,теперь, равенство дуги окружности отрезку , получим параметрические уравнения искомой траектории

, .

2.3. Лемниската Бернулли. Лемнискатой называется геометрическое место точек плоскости, для каждой из которых произведение расстояний от двух фиксированных точек, называется фокусами, равно квадрату половине межфокусного расстояния.

Пусть фокусы, произвольная точка лемнискаты. Тогда

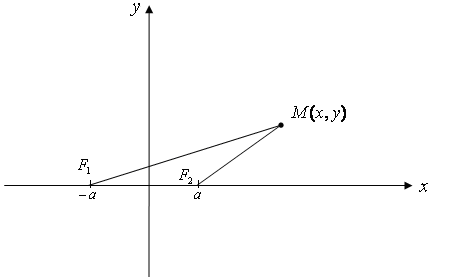
Выберем систему координат указанным на рисунке образом. Тогда

и, после исключения иррациональности, путём проведения очевидных преобразований, получим

Таким образом, кривая описывается алгебраическим уравнением 4-ой степени. Если же перейти к полярным координатам, получим,

,

или , после сокращения,-

.

Это более простая и употребительная форма уравнения лемнискаты Бернулли. Её график следующий

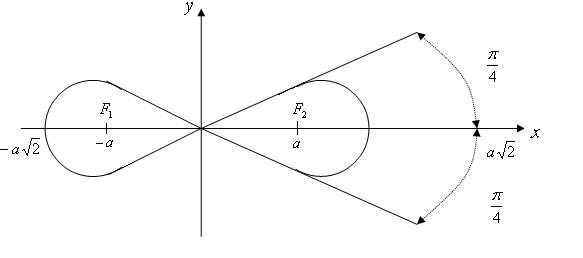
2.4. Кардиоида. Кардиоидой называют траекторию точки, расположенной на окружности некоторого радиуса , которая катится без скольжения по внешней части окружности равного ей радиуса.

Предположим, что центр неподвижной окружности совпадает с началом декартовой системы координат, начальное положение исследуемой точки совпадает с и выберем параметр указанным на рисунке образом.

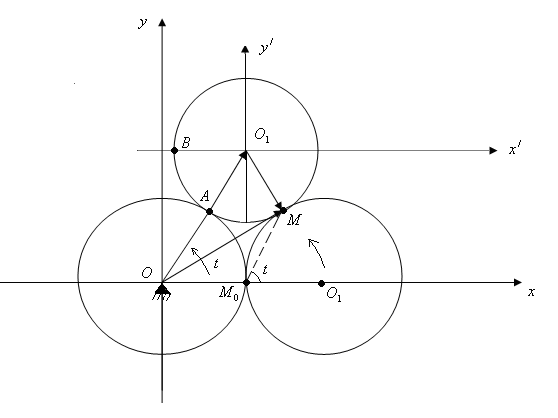
Тогда, в силу параллельности осей и имеем = = , а в силу равенства дуг и = = . Тогда точка в системе имеет координаты ,а координаты точки в системе , или .Учитывая теперь, что = + , получим координаты точки в системе

,

которые представляют собой параметрические уравнения кардиоиды в системе координат .

Полученные уравнения можно упростить, если перейти к полярным координатам, взяв в качестве полюса точку . Тогда координаты точки

в промежуточной системе равны

.

Выполнив тригонометрические преобразования и переходя ,в полученных соотношениях, к углу , получим

.

Обозначим теперь через и учтём , что ,тогда в полярных координатах получим

.

В системе кардиоида имеет следующий график

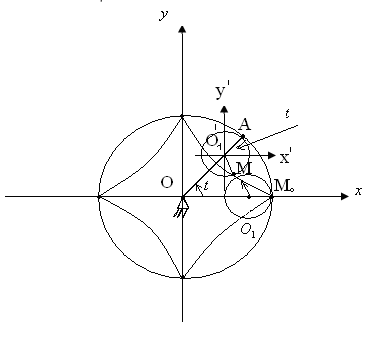
2.5. Астроида. Астроидой называется траектория точки, расположенной на окружности некоторого радиуса, которая катится без скольжения по внутренней части окружности в четыре раза большего радиуса.

Пусть радиус неподвижной окружности равен подвижной , . Выберем указанным на рисунке образом координаты, где - начальное положение подвижной точки , параметр и рассмотрим произвольное положение подвижной окружности. Тогда координаты точки равны

. В силу равенства дуг , и указанного соотношения радиусов окружностей

= 4 . Тогда = 3 , а координаты точки в сопутствующей системе координат равен ( ). Далее, в силу того, что

= + , координаты подвижной точки в системе равны

.

Проводя ,теперь, традиционные тригонометрические преобразования и переходя к простому аргументу, получим выражения,

х= , y= ,

которые представляют собой параметрические уравнения астроиды , а после исключения параметра t , её уравнение в декартовых

+ = .