3. Смешанное произведение векторов

Смешанным произведением векторов , , называется скалярное произведение векторного произведения первых двух векторов на третий. Т.е., смешанное произведение равно ( ) .

Так как смешанное произведение содержит скалярное и векторное произведение, то она обладает свойствами и первого и второго. Так, например,

( ) = - ( ) с

или

( ) = ( ).

Геометрический смысл ( ) . Рассмотрим одно из возможных расположений векторов

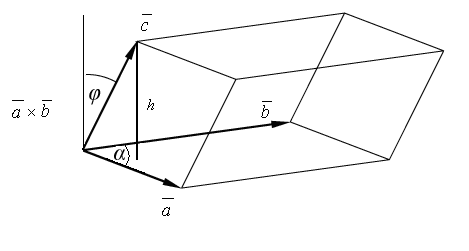
Имеем,

( ) |=| | | | соs . (3)

Но | | соs = h, длина перпендикуляра, опущенного из конца вектора на плоскость векторов и . Поэтому численное значение выражения (3), равно объёму призмы, построенной на векторах , , как на сторонах.

Если учесть, что угол может лежать в диапазоне ( , ), окончательно имеем, что модуль смешанного произведения равен объёму призмы, т.е.

V = | ( ) |.

Отсюда, - объём тетраэдра, построенного на этих векторах

V = | ( ) |.

Сделаем здесь следующее замечание.

Если предположить, что векторы , , лежат в одной плоскости, то, очевидно, V = 0, и , следовательно, смешанное произведение равно 0. Очевидно, верно и обратное. То же самое справедливо и для векторов, расположенных в параллельных плоскостях. Т.о. смешанное произведение векторов, расположенных в одной или параллельных плоскостях, такие векторы называются компланарными, равно нулю. Эта особенность является признаком компланарности векторов.

Выражение смешанного произведения через координаты. Пусть

= ( , , ), =( , , ), = ( , , ). Тогда

( ) = =

- + ) ( + + )=

= - + = .

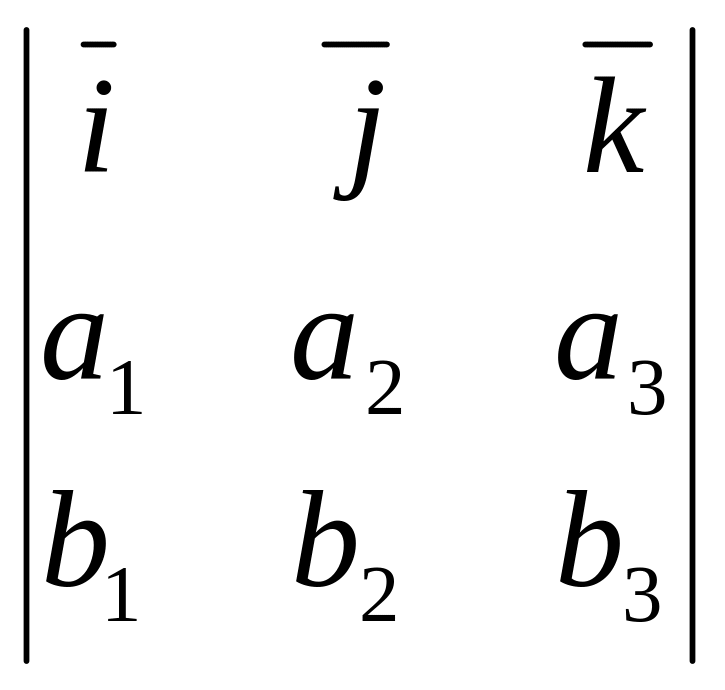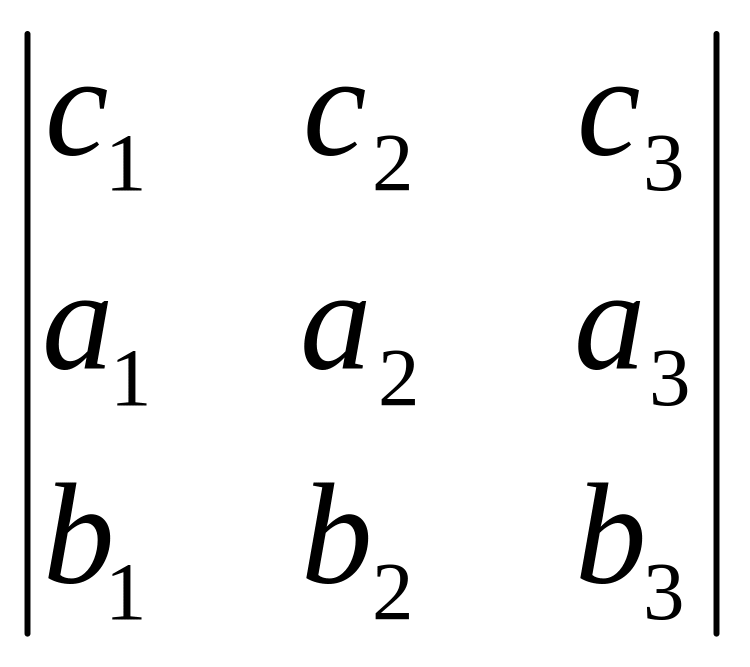Переставив .теперь, дважды первую строку , получим

( ) = .

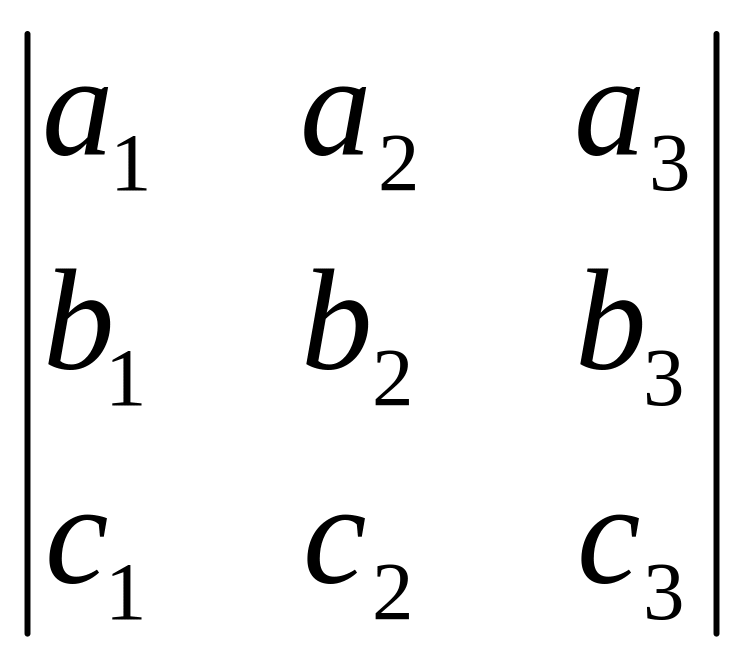Из этого соотношения вытекает следующее следствие . Переставляя строки в последнем определителе, получим , что

( ) =( ) = ( ) .

Данное равенство говорит о том, что порядок расположения знаков и в последовательности векторов не имеет значения и поэтому, иногда, смешанное произведение обозначают в виде . А вся система соотношений показывает, что при таких перестановках векторов, они называются циклическими, значение смешанного произведения не изменяется. Т.е.

= = .

Задача. Вычислить объём тетраэдра с вершинами в точках А (1,-1,2), А (2,1,2), А (1,1,4), А (6,-3,8) и его высоту опущенную из вершины А на грань А А А .

Решение. Образуем векторы

=

=

=

Тогда объём V тетраэдра А А А А равен

V= ,

т.е.

V= =6

Определим теперь площадь S грани А А А .Имеем

S= ,

т.е.

S= = =

Учтём теперь , что

V= S Н ,

где Н - высота тетраэдра, опущенная из вершины А .

Отсюда,

Н = = = .

Ответ: V= 6 , Н = .

Лекция 9. Элементы аналитической геометрии

Ниже рассматриваются уравнения прямой , плоскости и некоторых из основных задач, связанных с ними.

1. Плоскость в пространстве

К числу основных принадлежат следующие формы уравнений.

1.1. Каноническое уравнение. Получается в результате решения задачи о составлении уравнения плоскости, проходящей через заданную точку М₀ (x₀,y₀,z₀), перпендикулярно заданному вектору Вектор в этом случае называется нормальным.

Пусть точка М (x,y,z), – произвольная точка искомой плоскости Р. Тогда

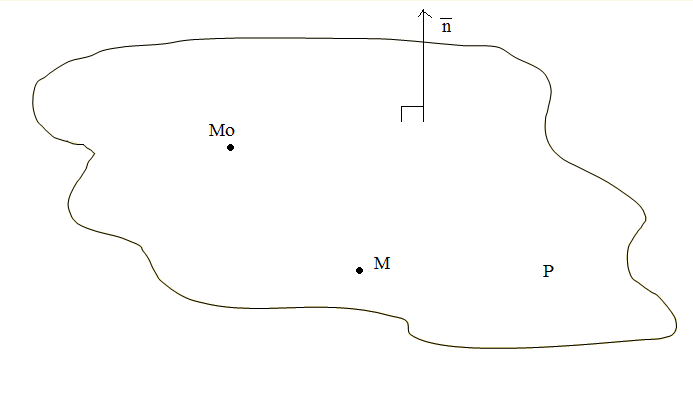
вектор и .Следовательно, скалярное произведение . Отсюда

A(x-x₀)+B(y-y₀)+C(z-z₀)=0. (1)

Соотношение (1) и называется каноническим уравнением плоскости.

1.2. Общее уравнение плоскости. Рассмотрим уравнение (1), выполним очевидное преобразование

Ax+By+Cz-(Ax₀+By₀+Cz₀)=0

и обозначив

D= - (Ax₀+By₀+Cz₀),

получим

Ax+By+Cz +D=0 , (2)

- общее уравнение плоскости.

1.3. Уравнение плоскости, проходящей через три точки . Предположим, что указанные точки не лежат на одной прямой. В этом, случае, согласно одной из аксиом стереометрии, можно провести плоскость и притом только одну.

Пусть даны три точки М₀ (x₀,y₀,z₀), М₁ (x₁,y₁,z₁), М₂ (x₂,y₂,z₂). Рассмотрим произвольную точку М(x,y,z), принадлежащую искомой плоскости Р. Рассмотрим векторы

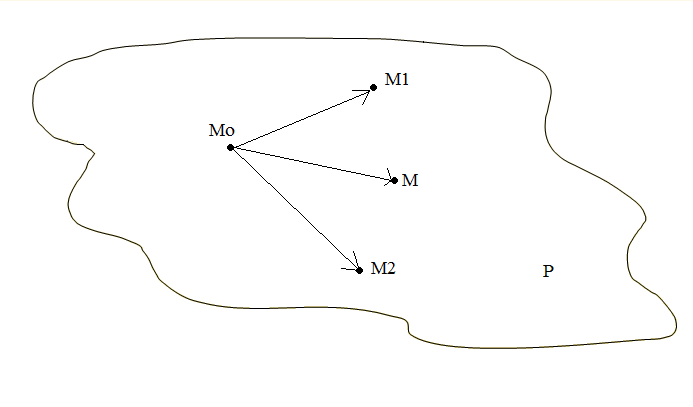
, и . Они компланарны, поэтому их смешанное произведение равно 0. Отсюда

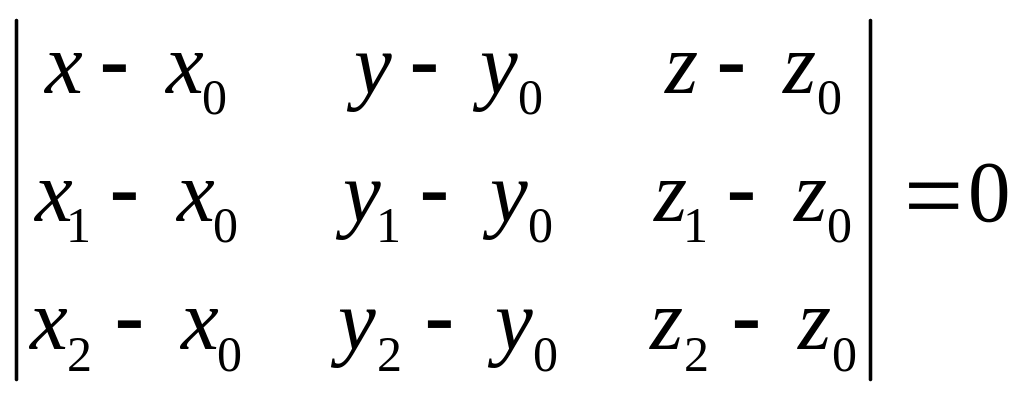. (3)

Соотношение (3) и представляет собой искомое уравнение.

Замечание. Если определитель в (3) тождественно равен 0, то это означает, что точки М₀, М_1, М₂ лежат на одной прямой. В этом случае задача имеет бесчисленное множество решений и можно ставить задачу о нахождении уравнения пучка плоскостей , проходящих через прямую М₀М_1.