Лекция 6. Линейный оператор, его матрица, преобразование

6.1.Определения

Пусть некоторое векторное пространство разности n над полем K, вектора , , … , - его базис. Предположим, что в задано отображение , ставящее в соответствие каждому вектору единственный вектор x, удовлетворяющее следующему условию

(αx+βy)=α x+β y,

В этом случае отображение называется линейным оператором, а вектор - образом вектора. Предположим, что известны разложения образов базисных векторов в базисе т. е.

= = …

= = …

. . . . . . . . . . . . . . . . . (1)

= = … ,

или

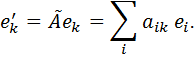
Обозначим через матрицу коэффициентов этих разложений, т.е.

=

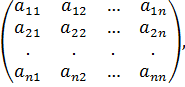
Она называется матрицей оператора . Оказывается, что её наличия вполне достаточно, для определения образа любого вектора.

Действительно, пусть ( ,-произвольный вектор. Определим = . Имеем

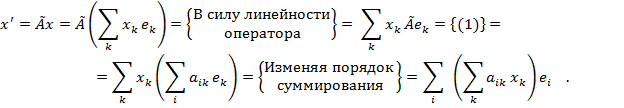
Отсюда, в силу единственности разложения вектора по базису, имеем

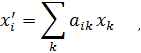
т.е координата образа равна произведению -ой строки матрицы на вектор . Т. о. в матричной форме

= , (2)

т.е. матрица полностью определяет действие оператора в пространстве

Очевидно, каждый линейный оператор единственным образом определяет матрицу , но верно и обратное, - каждой квадратной матрице соответствует некоторый оператор. Если во множестве линейных операторов ввести операции сложения, умножения и умножения на число естественным образом, а именно:

2.

3.

то им соответствуют матрицы +B, В,

2. Преобразование матрицы оператора при изменении базиса

Согласно (1), матрица оператора определяется выбором базиса. Установим закон её преобразования при изменении базиса.

Пусть в базисе оператор имеет матрицу А, в базисе , -матрицу , Т- матрица перехода. Обозначим через , некоторый произвольный вектор в базисах , соответственно, его образ, - через , . Составим систему соотношений

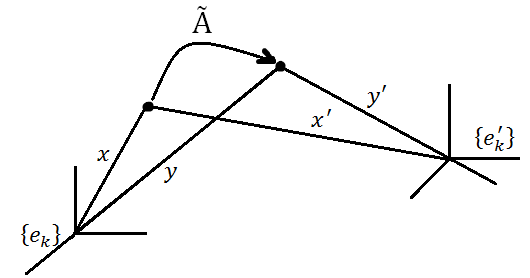
(3)

Откуда, выполняя указанные в (3) подстановки, получим

или

Сравнивая правые части полученных равенств, получим следующее соотношение

(4)

которое и описывает закон преобразования матрицы линейного оператора при изменении базиса пространства.

2. Задачи

Задача 1. Показать линейность и найти матрицу оператора проектирования пространства. на плоскость .

Решение.1. Рассмотрим рисунок, схематично описывающий условие задачи

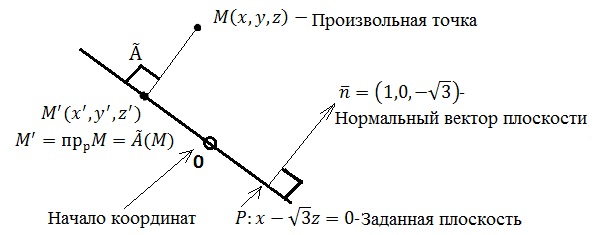
Образуем векторы Очевидно, что

т.к. , то Тогда

=

или

2. Определим значение параметра .

Т. к. , то

или

Отсюда

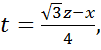
тогда

=

Таким образом, определена точка

3. Пусть матрица. Тогда

= .

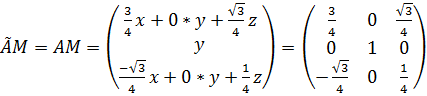
Таким образом

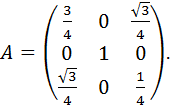
4. Т. к.

то -линейный оператор.

Задача 2.Найти область значений и ядро оператора из задачи 1.

Решение:

Определение. Множество векторов называется ядром оператора. Т.е. ядро оператора L,

1. Найдем ядро оператора.

Векторы, входящие в него, удовлетворяют уравнению

где 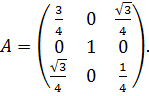(5)

Т. к. определитель система (5) имеет нулевые решения. Опишем их множество.

Имеем

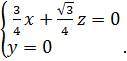
Отсюда Т. о.

2. Определим область значений оператора.

Т. к. действие оператора заключается в ортогональном проектировании точек пространства на плоскость то область его значений представляет множество всех точек плоскости т. е. множество точек

Ответ: Ядро область значений

Задача 3. Найти матрицу оператора в базисе где

Если в базисе она имеет вид

.

Решение. 1. Определим матрицу перехода

Согласно определения (см. Лекция 5) имеем

2. Используя (4) определим матрицу оператора в базисе

Имеем

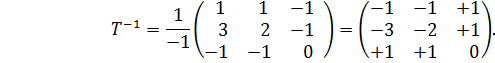
Тогда

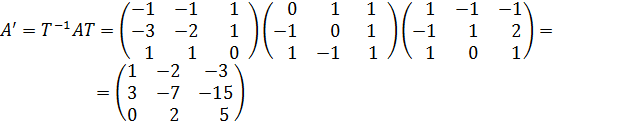
Ответ: .

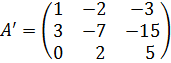Задача 4. Пусть

Найти .

Решение.1. Найдем матрицы операторов

Имеем

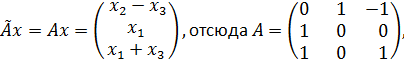
2. Найдем

Имеем

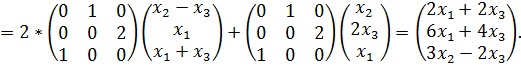
Ответ: .
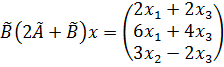