3. Преобразование координат при изменении базиса

Рассмотрим два базиса и , предположим, что некоторый вектор, имеет в них координаты и , соответственно. Установим связь между этими наборами.

Предположим, что известны разложения

векторов по базису . Матрица

,

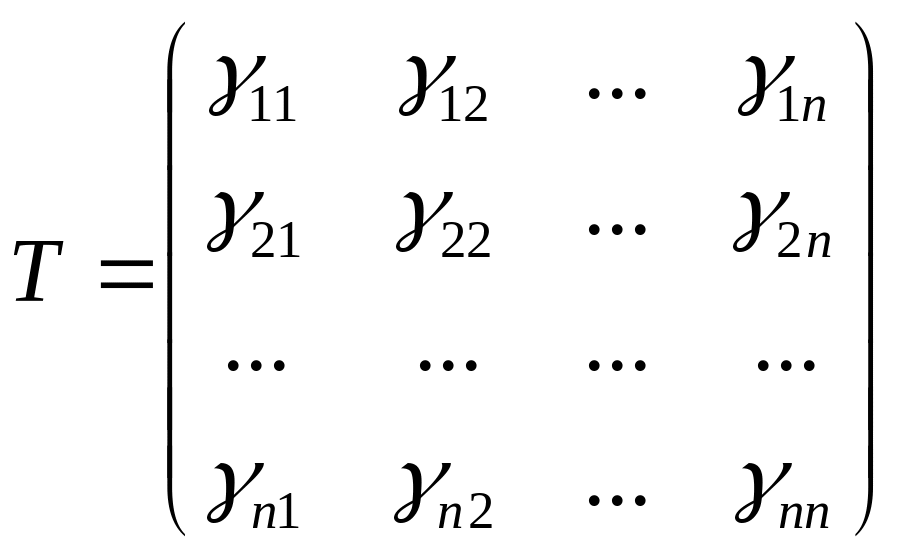состоящая из коэффициентов этих разложений, называется матрицей перехода. Тогда справедлива следующая система соотношений :

В силу единственности разложения вектора по базису (п. 5.2) , имеем

,

т.е. я координата вектора в базисе равна произведению i-ой строки матрицы Т на вектор Т.о. имеем

(3)

или

(4)

Соотношения (3), (4) и описывают закон преобразования координат при изменении базиса пространства. Заметим, что всегда существует, т.к. , в силу того, что совокупность векторов линейно независима.

4. Задачи

Задача 1. Дано векторное пространство, натянутое на векторы

, ,

, .

Определить его базис и размерность.

Решение. Элементами этого пространства являются векторы

,

где - заданному числовому полю. Базисом пространства является набор линейно независимых векторов из этой совокупности.

1. Определим размерность пространства.

Она равна рангу системы векторов ,который в свою очередь равен рангу матрицы

,

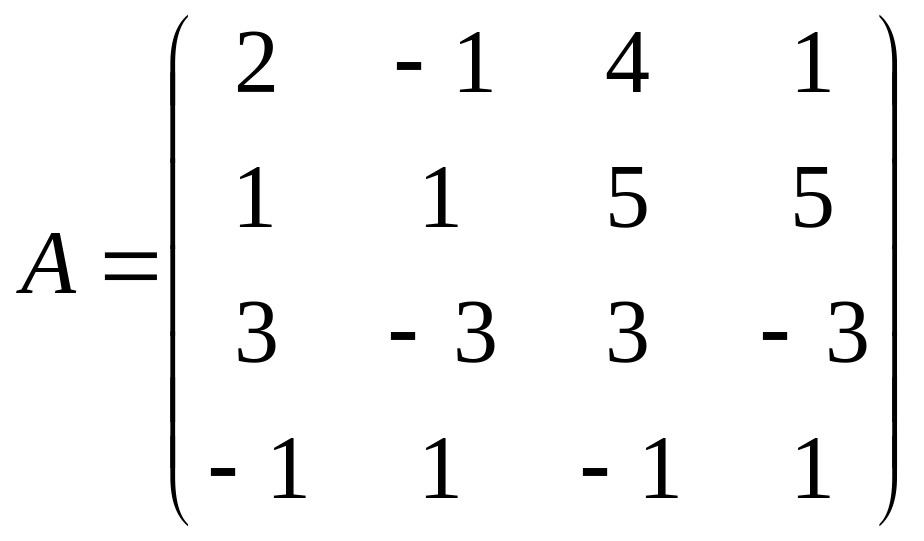столбцами (или строками) которой являются данные векторы. Проведя преобразования, имеем

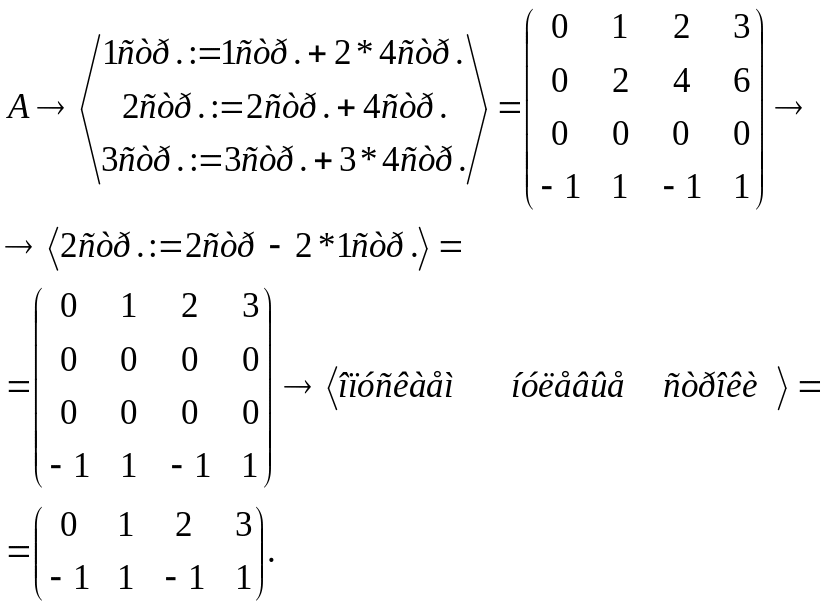
Т.к. определитель

,

следовательно, и размерность пространства равна 2.

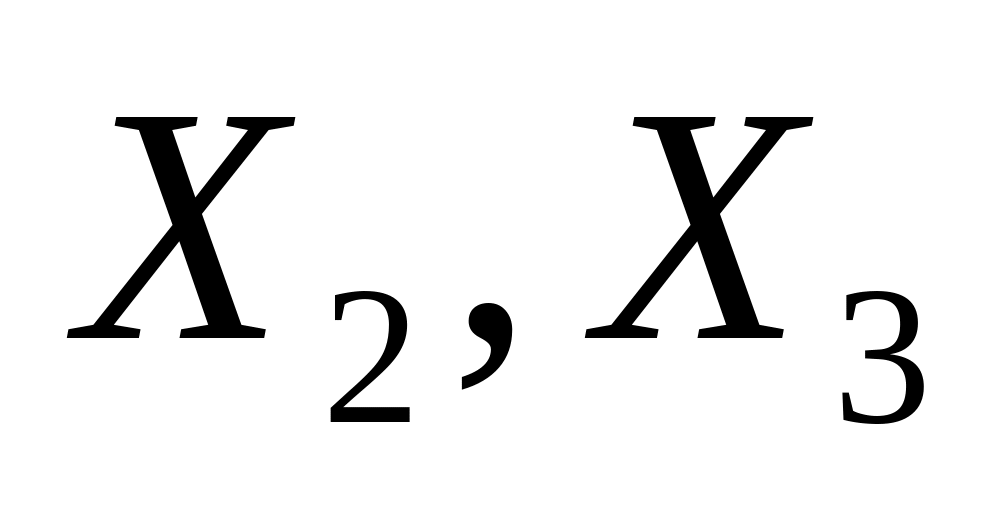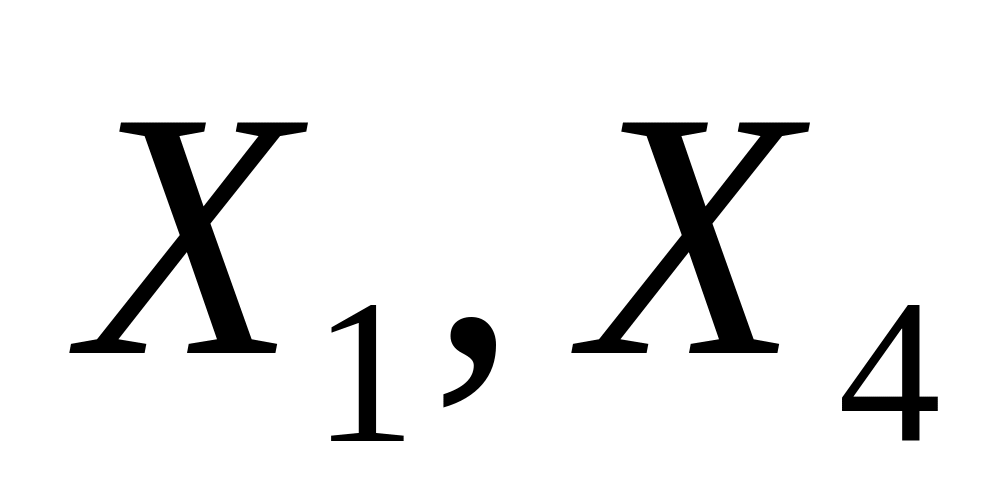2. Выполненные преобразования показывают, что векторы являются линейными комбинациями векторов . Поэтому, в качестве базиса пространства может быть выбрана эта система векторов.

Ответ: Размерность пространства равна 2. Вектора образуют базис.

Задача 2. Найти формулы преобразования координат при переходе от базиса

, , ,

к базису

, , , .

Решение.

1. Составим матрицу перехода Т.

В данном случае координаты векторов , равны коэффициентам их разложений базиса , поэтому имеем

.

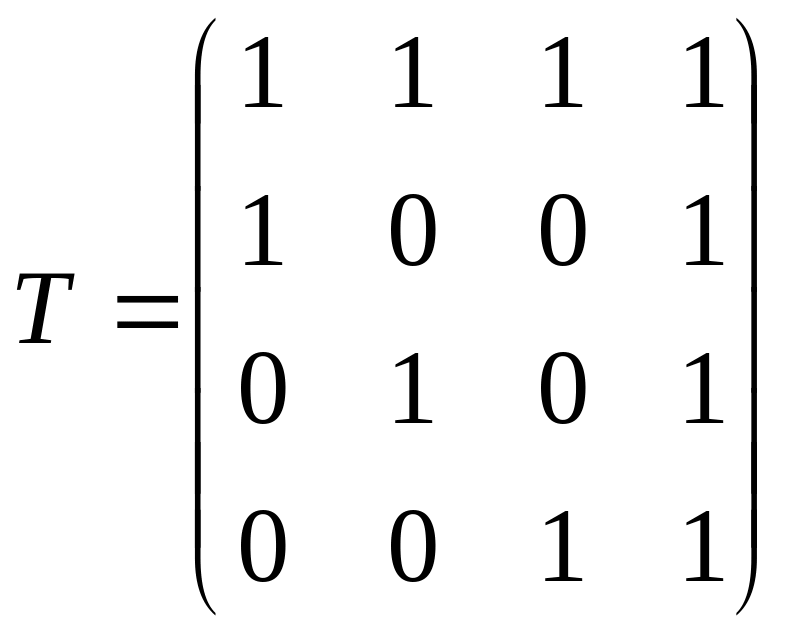2.Определим формулы преобразования координат.

Пусть - вектор в базисе , а - тот же вектор в базисе . Тогда согласно (3) , (4) имеем , или в развернутом виде

Это и есть искомый результат.

Разрешив последнее соотношение относительно , при желании можно получить формулы, выражающие координаты вектора через координаты вектора .

Ответ:

Задача 3. Уравнение «поверхности» в некотором базисе имеет вид Найти уравнение этой же поверхности в базисе

, ,

, .

Координаты векторов даны в базисе .

Решение .1. Представим уравнение поверхности в матричном виде.

Обозначив , имеем

, (5)

где

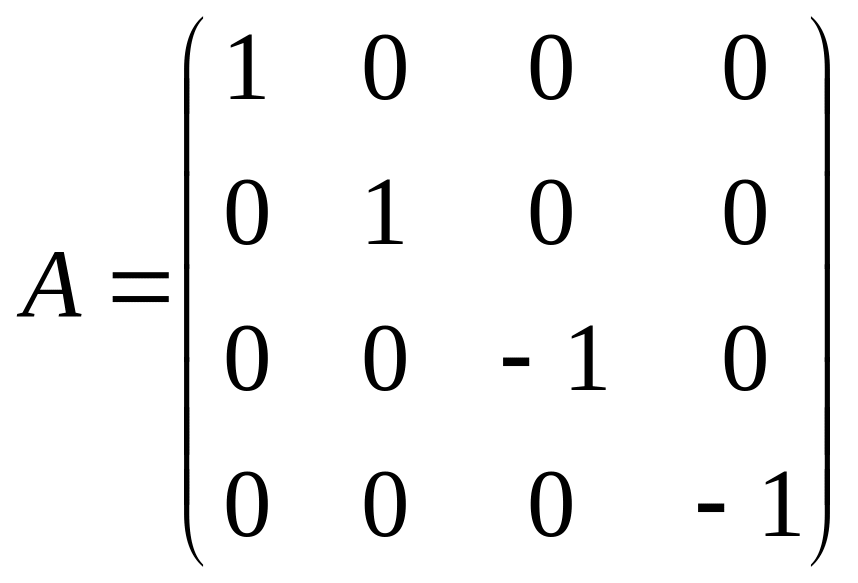
2.Составим формулу преобразования координат.

В данном случае, матрица перехода Т имеет вид:

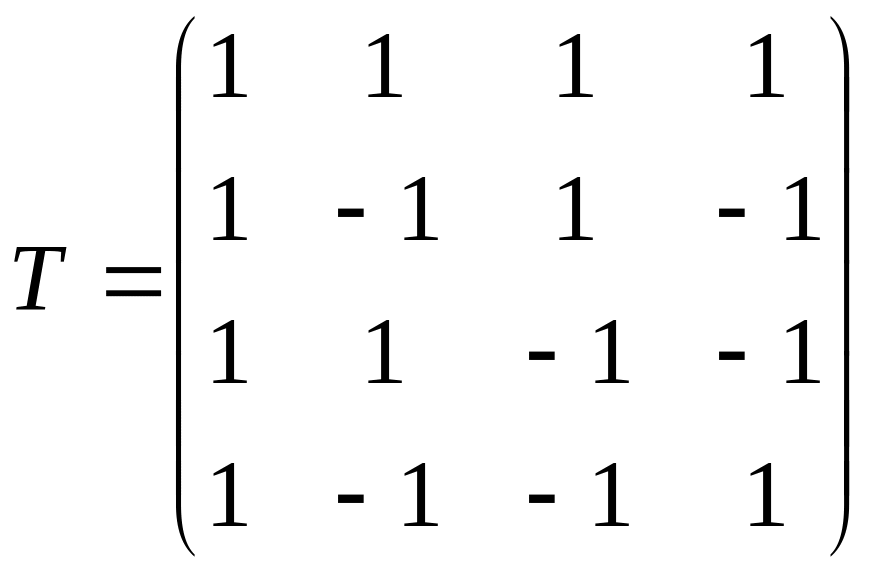
Тогда

. (6)

3.Определим уравнение поверхности в базисе .

Подставив (6) в (5 ), имеем

,

или

,

или

,

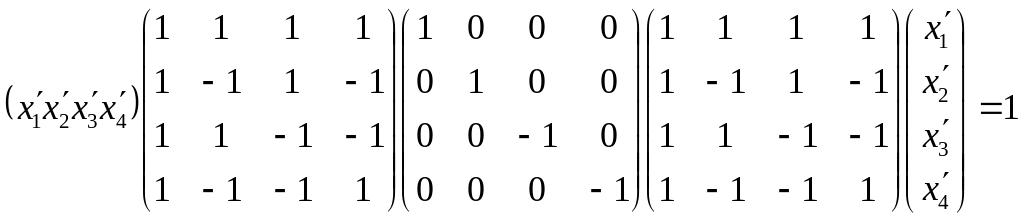или

,

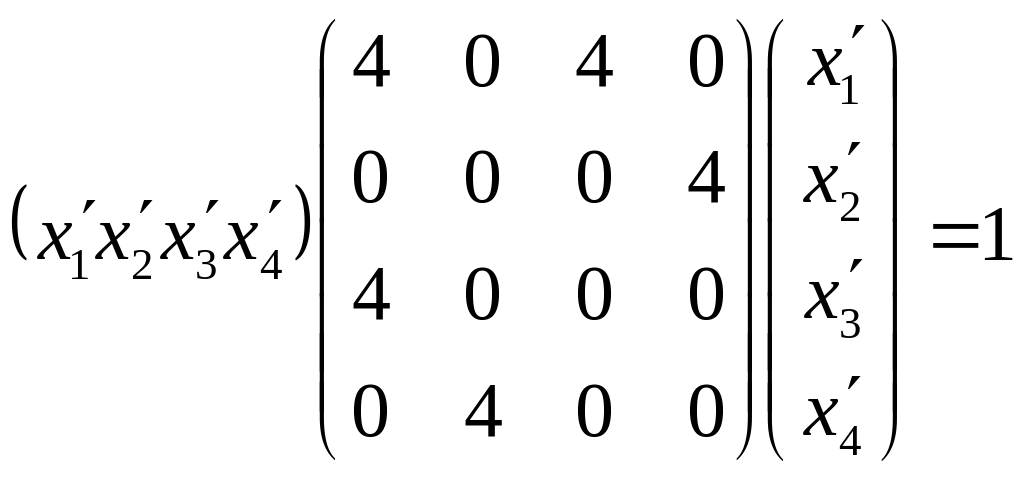или , окончательно,

.

Ответ: