Питання та завдання для самоперевірки

1. Обчисліть детермінант матриці

а) за правилом трикутників;

б) за правилом Сарюсса;

в) методом перетворень.

2. Обчисліть детермінант матриці . Чи можливо знайти його без використання правил трикутників або Сарюсса та перетворень?

3. При якому значенні детермінант дорівнює нулю?

4. При якому значенні детермінант дорівнює нулю?

5. Перевірте виконання рівності: , якщо:

.

6. Сформулюйте властивості детермінантів. Доведіть будь-які дві з них.

4. Доповняльний мінор та алгебраїчне доповнення

Означення 1.18 Доповняльним мінором елемента квадратної матриці називається детермінант матриці, що утворюється викресленням

-ого рядка та -ої колонки початкової матриці.

Приклад.

Означення 1.19 Алгебраїчним доповненням (ад′юнктою) елемента квадратної матриці називається доповняльний мінор цього елемента, знак якого визначається за формулою:

(1.4.)

Приклад.

Зауважимо, що доповняльні мінори та алгебраїчні доповнення обчислюються з використанням детермінантів, порядок яких на одиницю менший від порядку матриці.

Теорема 1.1 (т. Лапласа про розклад детермінанта)

Детермінант квадратної матриці можна обчислити як суму добутків елементів будь-якого її рядка або колонки на відповідні алгебраїчні доповнення:

, (1.5.)

(1.6.)

(Без доведення)

Теорема Лапласа дозволяє обчислювати детермінант будь-якого порядку. Якщо ми маємо детермінант -ого порядку, то за теоремою його можна обчислити як суму детермінантів ( )-ого порядку. У свою чергу ці детермінанти можна розкласти на детермінантів -ого порядку і так далі, аж доки ми не отримаємо детермінанти третього або другого порядків, які можна обчислити за алгоритмами, що наведені вище.

Приклад.

Теорема 1.2. Сума добутків елементів будь-якого рядка або колонки на алгебраїчні доповнення до елементів іншого рядка або колонки дорівнює нулю.

(1.7.)

(1.8.)

Доведення. Розглянемо (1.7.). Ліва частина при порівнянні з теоремою Лапласа (формула 1.5.) дорівнює детермінанту матриці, у якої на місці -ої колонки розташована -та колонка. При цьому -та колонка залишається на місці. Отже, у цій матриці дві однакові колонки і за п’ятою властивістю детермінантів, детермінант дорівнює нулю. Аналогічно доводиться (1.8.).

Детермінант є важливою характеристикою матриці, причому в багатьох випадках принциповим є питання: дорівнює він нулю чи ні.

Означення 1.20. Квадратна матриця називається виродженою, якщо її детермінант дорівнює нулю. У протилежному випадку матриця називається невиродженою.

1.5. Обернена матриця

Розглядаючи дії над матрицями, ми зазначали, що віднімання, як обернена операція до додавання, відсутня. Але цю дію можна зробити за допомогою двох операцій. Операції, оберненої до операції добутку матриць, не існує. Деякою аналогією ділення на множині квадратних матриць є операція обернення матриць. Це унарна операція.

Означення 1.21. Матриця В називається оберненою до матриці , якщо

,

де - одинична матриця. Позначається обернена матриця: . У даному випадку це не є степінь, читається так: «А мінус один».

Означення 1.22. Матриця , яка є транспонованою матрицею алгебраїчних доповнень елементів матриці , називається союзною до матриці .

(1.8.)

Знайдемо добуток матриці на союзну до неї матрицю справа: .

За означенням елемент матриці добутку обчислюється як сума добутків елементів -ого рядка лівої матриці на елементи -ої колонки правої:

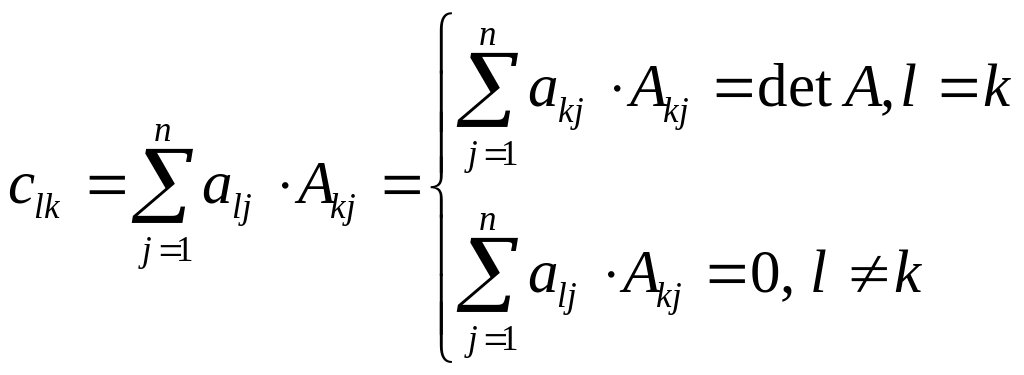
Коли ми знаходимо елементи матриці добутку з однаковими індексами ( ), тобто елементи, що утворюють головну діагональ, то отримаємо суму добутків якогось рядка на алгебраїчне доповнення елементів цього ж рядка. За теоремою Лапласа, це детермінант матриці (позначимо його ). А елементи, що не належать головній діагоналі ( ), є сумою добутків елементів деякого рядка матриці на алгебраїчні доповнення елементів іншого рядка союзної матриці. За теоремою 1.2 ця сума дорівнює нулю.

Таким чином, добуток являє собою діагональну матрицю, причому на головній діагоналі розташовані величини . Таким же буде добуток матриці на союзну зліва.

Теорема 1.3. Необхідна і достатня умови існування оберненої матриці.

Для того, щоб до квадратної матриці існувала обернена, необхідно і достатньо, щоб матриця була невиродженою.

Необхідна умова. Якщо існує обернена матриця , то , тобто - невироджена матриця.

Доведення. За означенням . Знайдемо детермінант лівої та правої матриць:

.

Детермінант добутку дорівнює добутку детермінантів, а детермінант одиничної матриці дорівнює одиниці (легко довести, що детермінант діагональної матриці дорівнює добутку елементів головної діагоналі, а оскільки в одиничної матриці всі елементи головної діагоналі дорівнюють одиницям, то ):

.

Припустимо, що матриця вироджена, отримаємо хибну числові рівність: 0=1, тобто протиріччя, яке встановлює, що припущення є хибним, Таким чином, твердження теореми є правильним: .

Достатня умова. Якщо матриця невироджена, то існує обернена до неї.

Доведення. Нехай матриця є невиродженою, . Якщо добуток помножити на величину , то ми отримаємо одиничну матрицю:

.

Таким чином, обернену матрицю можна знайти за формулою:

(1.9.)

А це зокрема означає, що обернена матриця існує.

Приклад. Розглянемо матрицю: .

Її детермінант, . Алгебраїчні

доповнення були знайдені раніше. Обернена матриця має вигляд:

Зробимо перевірку, тобто знайдемо добуток:

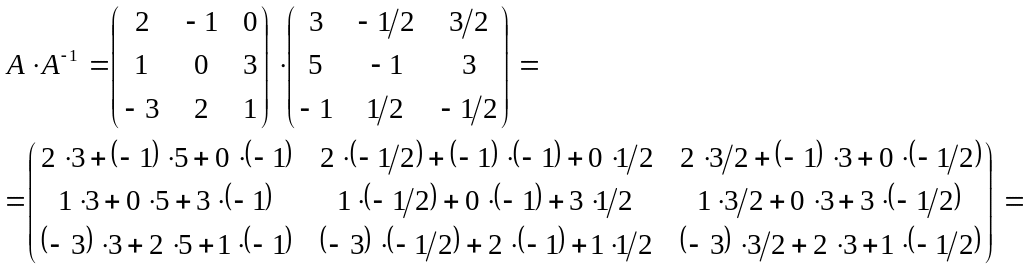
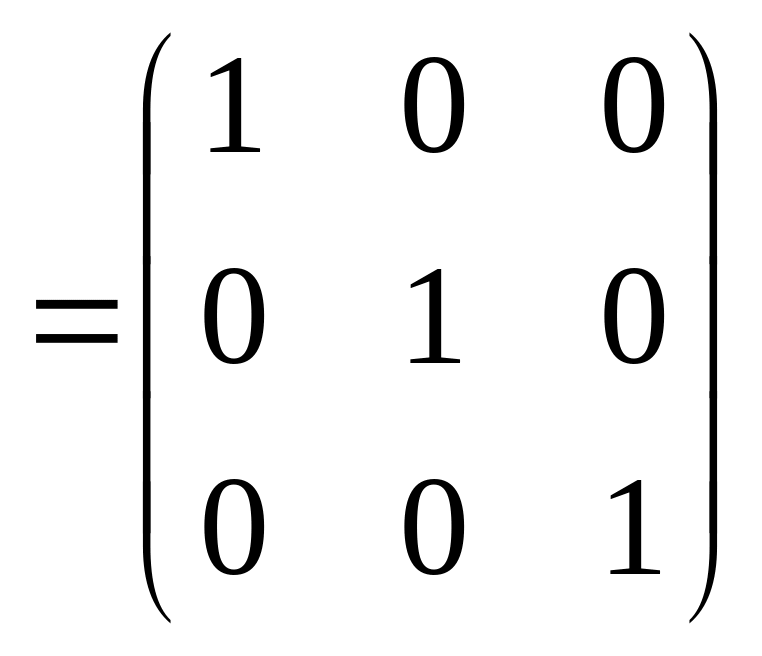. Оскільки ми отримали одиничну матрицю, то наші розрахунки правильні.