I. Блок динамики фондов банка

Уставный фонд UF(t + 1) в момент времени t +1 определяется его величиной в предыдущий период и отчислениями от прибыли банка прошлого момента времени N(t):

UF(t + 1) = UF(t) + Y₁ · N(t), (7.1)

где Y₁ – коэффициент отчислений из прибыли в уставный фонд (0 ≤ Y₁ ≤ 1).

Рисунок 7.1. Схема взаимодействия блоков имитационной модели

Суммарная величина прочих фондов OF(t + 1) (развития, дивидендов, специального, резервного и т.д.) определяется соответствующей их суммарной величиной и предыдущий момент времени, расходами прошлого периода и поступлениями их прибыли:

OF(t + 1) = (1 – ζ₁) · OF(t) + (1 - Y₁) · N(t), (7.2)

где ζ₁ – расходы прошлого периода, в том числе выплаты дивидендов, покрытие убытков, финансирование развития и т.д. (0 ≤ ζ₁ ≤ 1).

Собственный капитал банка SK(t + 1) представляет собой сумму всех фондов банка (включая фонды экономического стимулирования, уставный и резервный фонды и др.):

SK(t + 1) = UF(t + 1) + OF(t + 1). (7.3)

Защищенный капитал банка ZK(t + 1) определяется прошлыми запасами (золото, валюты и т.д.) и новыми поступлениями из прибыли:

ZK(t + 1) = ZK(t) + Y₂ · N(t), (7.4)

где Y₂ – коэффициент отчислений в фонд защищенного капитала (0 ≤ Y₂ ≤ 1).

ными частями, причем ставки IF_i(t) и IU _i(t) приняты на момент предоставления кредита.

Заметим, что величина ηF₂ , ηU₂ …, ηF₄ , ηU₄ могут быть определены как на основе статистической обработки материала, так и с учетом классического соотношения, связывающего риск и процентную ставку. Если предположить, что вероятность невозврата кредита , , , а безрисковая ставка процента I_бр(t + 1) равна ставке по депозитам до востребования, скорректированной на среднюю банковскую маржу M[I_бр(t + 1) = r₂ (t +1)+M], то из условий и при известных фактических ставках и могут быть определены велечины и , а также ηF_i и ηU_i.

Просуммировав возвращенные суммы кредитов физических и юридических лиц для различных видов активов, получим

Воз SA(t +1) = Воз SAF(t +1) + Воз SAU(t +1), (7.53)

Воз NA₁(t +1) = Воз NAF₁(t +1) + Воз NAU₁(t +1), (7.54)

Воз NA₂(t +1) = Воз NAF₂(t +1) + Воз NAU₂(t +1). (7.55)

Общая величина возврата записывается в следующем виде:

Воз AО(t +1) = Воз SA(t +1) + Воз NA₁(t +1) + Воз NA₂(t +1) = Воз AF(t+1) + Воз AU(t +1), (7.56)

Где Воз AF(t+1) и Воз AU(t +1) – общие возвраты активов, предоставленных физическим и юридическим лицам.

Фактическое распределение свободных ресурсов определяется минимальной среди двух величин: внутренних свободных ресурсов банка Вн Res(t+1) и потребностей в кредитно-инвестиционных ресурсах, обусловленной внешней средой (другими хозяйственными субъектами) Кр(t+1):

Res(t+1) = min { Вн Res(t+1),Кр(t+1)}. (7.57)

Когда потребность в кредитно-инвестиционных ресурсах являются лимитирующими, например, ввиду общего спада производства и снижения благосостояния населения, имеем

Кр(t+1)< Вн Res(t+1). (7.58)

Если Кр(t+1) считается заданной величиной, получаемой либо на основе экспертных оценок, либо аналитическим путем, то может быть рассчитана величина остатка кредитно-инвестиционных ресурсов АКр(t+1), направляемых в фонд альтернативного размещения:

4. Формирование дополнительных условий задачи оптимизации( геп, резервный фонд, спрос на кредиты)

Для расчета гепа требуется определить чувствительные к изменению ставки процента активы и пассивы в (t+1)-м периоде. Рассмотрим активы, переданные (размещенные) физическим лицам:

LAF(t +1) = LAF(t) + (1 – rf₁)* XF₁(t +1), (7.59)

SAF(t +1) = SAF(t) + (1 – rf₂)* XF₂(t +1) – Воз SAF(t +1), (7.60)

NAF₁(t +1) = NAF₁ (t) + (1 – rf₃)* XF₃(t +1) – Воз NAF₁ (t +1), (7.61)

NAF₂(t +1) = NAF₂ (t) + (1 – rf₄)* XF₄(t +1) – Воз NAF₂ (t +1). (7.62)

Здесь rf₁ , rf₂ , rf₃ и rf₄ - доли отчислений в резервный фонд, определяемые нормативными документами Банка России и пропорциональные объему средств, направленных в данные виды активов; LAF(t) – величина остатка ценных бумаг, не подлежащих реализации в силу наступления срока погашения либо по другим причинам:

LAF(t) = [1 – α_цб(t +1)]*V_цб(t)* (t), (7.63)

или

LAF(t +1) = П_цб(t +1),

где П_цб(t +1) – покупка ценных бумаг.

Суммарные активы, размещенные физическими лицами, составят

Sum AF(t +1) = LAF(t) + SAF(t) + NAF₁(t) + NAF₂(t) + * XF_i(t +1) – Воз AF(t +1). (7.64)

Аналогично суммарные активы, размещенные юридическими лицам, составят

Sum AU(t +1) = LAU(t) + SAU(t) + NAF₁(t) + NAU₂(t) + * XU_i(t +1) – Воз AU(t +1). (7.65)

Итак, активы, чувствительные к изменению ставки процента АЧП(t+1), представляют собой сумму соотношений (7.64) и (7.65) без ликвидных активов LAF(t) и LAU(t).

Введя обозначение

A(t) = SAF(t) + NAF₁(t) + NAF₂(t)– Воз AF(t +1) + + SAU(t) + NAF₁(t) + NAU₂(t)– Воз AU(t +1),

получим

АЧП(t+1) = А(t) + * XF_i(t +1) + * XU_i(t +1). (7.66)

Пассивы, чувствительные к изменению ставки процента ПЧП(t+1), представляют собой сумму переменных, выраженных соотношениями (7.7), (7.8), (7.11), (7.12), (7.14) и (7.21) с учетом депозитных резервов (фонд обязательных резервов):

ПЧП(t+1) = P_цб(t+1) +OV(t+1) + MB₁(t+1) + MB₂(t+1) +VD₁(t+1) + VD₂(t+1). (7.67)

Для успешного (безубыточного) функционирования банка в условиях снижения ставки процента, характерного для периода стабилизации, необходимы: 1) либо регулярный пересмотр банком ставки процента по вкладам в зависимости от сложившийся конъюнктуры (как это делает, например, Сбербанк России); 2) либо (что более правильно, так как соответствует нормам цивилизованного бизнеса) поддержание отрицательного гепа[162], что, правда, более приемлимо в стабильной экономике при выполнении соотношения . При малых темпах снижения ставки процента целесообразно поддерживать геп в состоянии, близком к сбалансированному (приближение со стороны отрицательных значений).

Итак,

АЧП(t+1) – ПЧП(t+1) ≥ −δ(t+1), (7.68)

где δ(t+1) – заданное малое положительное число.

С учетом соотношений (7.64) – (7.66) получаем условия, которым должны удовлетворять искомые переменные XF_i(t +1) и XU_i(t +1):

* XF_i(t +1) + * XU_i(t +1) ≤

≤ПЧП(t+1) – A(t) −δ(t+1). (7.69)

Соотношение (7.69) характеризует управление гепом и может рассматриваться в качестве дополнительного ограничения оптимальной задачи (7.45).

Аналогичным образом задача (7.45) может быть расширена за счет введения ограничительного условия для величины резервного фонда RF(t+1), который должен быть не меньше, чем заданный уровень RF(t+1):

RF(t+1) = RF(t) + * XF_i(t +1) + * XU_i(t +1) + AKp(t+1) – (1 – ηF₂ )*Воз SAF(t) – (1 – ηF₃ )*Воз NAF₁(t) – (1 – ηF₄ )*Воз NAF₂(t) ≥ RF(t+1). (7.70)

Последние три слагаемых в левой части соотношения (7.70) отражает процесс компенсации невозврата кредита в t-м периоде.

Важным условием является учет спроса на кредиты, который считается в данной модели зависящим от динамики кредитной ставки процента. Для аналитической оценки спроса могут быть использованы обратно пропорциональные зависимости, вид которых противоположен функциям, изображенным на рис. 7.2: если с ростом депозитной ставки процента наблюдается прирост вкладов, то с ростом кредитной ставки спрос на кредитно-инвестиционные ресурсы уменьшается, что отражено на рис. 7.3.

В соответствии с видом функции, показанной на рис. 7.3, можно записать следующие выражения для определения спроса на различные виды кредитно-инвестиционных ресурсов для физических и юридических лиц:

(7.71)

(7.72)

(7.73)

(7.74)

(7.75)

(7.76)

Здесь K₀SF,K_oNAF₁, K_oNAF₂, K_oSU, K_oNAU₁, K_oNAU₂,IF₀₂, IF₀₃, IF₀₄, IU₀₂, IU₀₃ и IU₀₄ – параметры зависимостей, получаемые эмпирическим путем.

Таким образом,

KрSАF(t+1) + KpNAF₁ (t+1) + KpNAF₂(t+1) + KpSAU(t+1) + KpNAU₁(t+1) + KpNAU₂ (t+1) + KрLАF(t+1) + KpLAU(t+1) = Kp(t+1) (7.77)

где KрLАF(t+1) и KpLAU(t+1) – прогнозируемый спрос на ценные бумаги со стороны физических и юридических лиц(государства) соответственно.

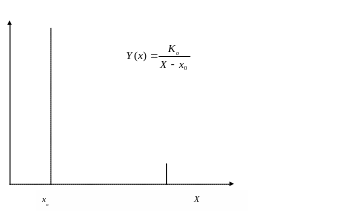
Рис. 7.3. Функция стимулирования спроса на кредиты в зависимости от процентной ставки кредита:

x₀ – минимально возможный уровень кредитной ставки (превышающий депозитную ставку);

- средняя нормативная эффективность вложений в промышленность, при которой спрос на кредитные ресурсы приближается к нулевому

К₀ - параметр функции, определяющий ее кривизну: Y(x) = K₁/(X-x₀)

Итак, соотношение (7.77) с учетом условия (7.57) формирует правую часть общего ресурсного ограничения оптимальной задачи (7.45). Кроме того, задача (7.45) дополняется следующими частными ограничениями по видам кредитно-инвестиционных вложений:

XF₂(t+1) ≤ Kp SAF(t+1), (7.71a)

XF₃(t+1) ≤ Kp NAF₁(t+1), (7.72a)

XF₄(t+1) ≤ Kp NAF₂(t+1), (7.73a)

XU₂(t+1) ≤ Kp SAU(t+1), (7.74a)

XU₃(t+1) ≤ Kp NAU₁(t+1), (7.75a)

XU₄(t+1) ≤ Kp NAU₂(t+1). (7.76a)

Б. Валютные операции

Система соотношений модели, описывающая валютные операции, дублирует систему (7.45) – (7.77), но с учетом валютных ресурсов. Соответствующие зависимости могут быть отражены подобно тому, как это сделано для валюты в блоке пассивных операций. Для краткости указанные зависимости здесь опускаются. Предполагается, что после определения величины валютных активов для рассматриваемого периода далее производится их конвертация в рубли, а затем основные показатели работы в банка рассчитывается в единой (национальной) валюте.