Методологические и методические вопросы моделирования банковской деятельности

Систематизация основных экономико-математических методов и моделей, используемых в банковской деятельности

Арсенал экономико-математических методов, применяемых для анализа банковской деятельности, весьма обширен и разнообразен. Первой работой, открывающей математическую теорию банковского дела, считается исследование Ф.Эджворта, изданное в 1988 г. Анализ эволюции и развития математической теории банков, приводимый в работе и охватывающий период с 1988 по 1991 г. включает более 60 наименований научных исследований, использующих самый широкий спектр экономико-математических моделей различных типов. К их числу относятся оптимизационные, вероятностные, статистические, равновесные и балансовые методы исследования операций, теории игр и т.д.

В гл.I было показано, что банк может быть рассмотрен как разновидность фирмы, функционирующей на рынке денег. В научной литературе данное обстоятельство нашло отражение в устоявшемся термине «банковская фирма». В связи с этим при моделировании деятельности банка наряду с другими методами правомерно использовать основные понятия и модели теории фирмы. Не случайным поэтому является значительный удельный вес в общем числе математических исследований именно моделей фирмы, адаптированных к специфике банковского дела.

Следует отметить, что банк представляет собой сложный объект моделирования, требующий прежде всего комплексного подхода. По мнению Н.Мэрфи, «трудно создать интегрированную модель банковской фирмы, которая одновременно охватывала бы управление ликвидностью, выбор портфеля активов, политику ценообразования и физический процесс производства.

В связи с этим наибольшее распространение имеют либо частные модели, описывающие конкретную сферу деятельности банка, либо обобщенные полные модели, которые хотя и отображают функционирование банка в целом, но делают это достаточно агрегированно.

Итак, можно выделить две основные группы моделей, описывающих банковскую деятельность, – частные и полные модели. Рассмотрим их.

Частные модели банковской деятельности

В группе частных моделей существуют два дивергентных направления. Они основаны на различных гипотезах о поведении банка на рынке денег и о его возможностях управления процессами спроса и предложения на этом рынке.

Первое направление исходит из гипотезы о малой управляемости рынка депозитов: банк только принимает денежные вклады, общий поток которых зависит от экономической ситуации в целом, благосостояния населения и других факторов, которые находятся вне сферы компетенции банка и поэтому должны считаться заданными экзогенно. Модели данного направления, сконцентрированные на анализе поведения финансовых агентов, действующих на рынке кредитов, и на взаимодействии банка с ними, базируются на теории формирования портфеля заказов (портфеля банковских активов), теории риска и т.д. и включают также оптимальные модели формирования структуры активов. В качестве примера приведем два варианта моделей такого типа.

Модель 1

В первой модели предполагается, что уже известны некоторые общие желаемые пропорции в структуре активов А_i, где i – индекс группы актива. В рамках каждой i–й группы требуется определить оптимальные объемы вложений x_ij по проектам j. Критерием оптимальности является общий получаемый доход, зависящий от эффективности проекта (вложения) l_ij.

≤ A_j, i =

x_ij ≥ 0, i = ; j =

max

(6.1)

Модель 2

Вторая модель отображает процесс формирования структуры активов с учетом:

1) наличия собственного капитала SK и привлеченных средств k-го вида G_k по депозитной ставке r ;

2) необходимых резервов, отчисляемых по норме r_i* для каждого вида актива А_i;

3) распределение долей х_ij активов i-того вида по проектам j.

Критерием оптимальности также является общий получаемый доход при известной эффективности проекта l_ij.

r_i*A_i – R_i ≤0, i =

x_ij, A_i, R_i ≥0, i = ; j =

max

(6.2)

Следует заметить, что в условиях переходного периода актуальным является включение в модели фактора риска. Так как переходные процессы обычно характеризуются, во-первых, высокими темпами инфляции и, во-вторых, нестабильностью экономических процессов и отсутствием устоявшихся правовых и этических норм бизнеса, то наиболее важными видами рисков являются риски процентной ставки и невозврата кредита; при этом при моделировании обычно применяется вероятностный подход.

Второе направление опирается на противоположную гипотезу. Полагают, что рынок кредитов слабо зависит от банковской деятельности: спрос на них и его структура считаются обусловленными инвестиционной активностью и заданными. Основное внимание концентрируется на рынке депозитов и факторах, обусловливающих их привлечение. Так как плата (проценты) за депозиты входят в состав банковских издержек, то исследования, соответствующие этому направлению, обычно тяготеют к теории издержек как части более общей теории фирмы.

Здесь возможны два подхода. В условиях стабильной и равновесной экономики, а также законченного «передела» сфер влияния банков предложение депозитов часто считается случайной величиной, а используемые модели характеризуются как вероятностные. В случае совершенной конкуренции процентная ставка по депозитам рассматривается как аргумент функции предложения средств, а банк – как покупатель денежных вкладов, который приобретает их по объявленной цене, причем вариация ставки считается эффективным инструментом осуществления накоплений населением. В этой ситуации важным является выбор вида зависимости объемов привлекаемых средств от уровня ставки процента. Иногда (как, например, в модели Сили) оба этих подхода сочетаются: рассматривается двухфакторная функция объемов депозитов от случайной величины и уровня ставки процента.

Для современного этапа становления банковской системы в России достаточно характерной является агрессивная стратегия банков на рынке депозитов, что подтверждается значительной дифференциацией ставки процента, рассматриваемой как основное орудие конкурентной борьбы за клиента. Так, в результате развернувшейся конкуренции Сбербанк России, проводивший осторожную процентно-ценовую стратегию по установлению депозитной ставки процента, потерял часть своих клиентов. Однако он остался монополистом в деле привлечения сбережений; его по-прежнему значительная доля в общей сумме вкладов, привлеченных банками, составила на 1 января 2001 года 75,2%. В то же время существенная часть банков в ходе этой конкурентной борьбы оказалась неплатежеспособной, так как выбор ими высоких ставок процента по депозитам не был подкреплен убедительными доводами.

При обосновании подобной агрессивной стратегии необходимо решать довольно сложную задачу сопоставления двух эффектов, возникающих из-за изменения депозитных ставок процента r^п:

1) влияние r^п на объем привлекаемых средств G (r^п);

2) изменения производственной функции F(G), или доходов банка, в зависимости от этого объема.

Соответствующие графики, приведенные на рис. 6.1, свидетельствуют о неоднозначности возможных решений. Так, с ростом депозитной ставки дальнейшего ожидаемого увеличения объема привлекаемых средств может не произойти (ввиду полного «освоения» имеющейся экономической ниши), а в ряде случаев наблюдается даже его снижение (утрата доверия вкладчиков при излишне высоких депозитных ставках процента). В то же время в соответствии с общими положениями теории фирмы производственная функция банка является монотонно возрастающей, выпуклой вверх функцией. Таким образом, следует ожидать наступления такого момента, при котором повышенные издержки банка, связанные с привлечением депозитов, не будет окупаться получаемыми доходами. Это обусловливает необходимость определения границ проведения агрессивной депозитно-аккумуляционной стратегии, что является предметом исследования экономико-математической задачи.

G (r^п) F(G)

r^п G

Рис.6.1. Зависимость объема депозитов G (r^п) от ставки процента r^п (а) и производственная функция F(G), отражающая эффект использования

депозитов (б)

М

G (r^п) ≤ µ · SK

r^п ≥0

max

атематическая нелинейная модель определения оптимального уровня депозитной ставки процента r^п при известной нелинейной функции G (r^п) и при выполнении необходимого соотношения между привлекаемыми средствами и собственным капиталом может быть записана следующим образом:

(6.3)

Здесь – производственная функция, определяющая суммарный доход в зависимости от объема привлеченного ресурса G (r^п) и кредитной ставки процента (параметр r^a);

µ - коэффициент допустимого объема привлеченных средств по отношению к собственному капиталу SK;

– процентные издержки, или произведение объема привлеченных средств на оптимальную депозитную ставку r^п;

при этом целевая функция максимизирует процентный доход банка.

Следует заметить, что другим вариантом поведения совокупности агрессивных стратегий на рынке депозитов является расширение экономического пространства путем создания сети филиалов. Однако и в этом случае повышаются банковские издержки, поэтому подобные решения также должны обосновываться с помощью экономико-математических моделей.

В работе отмечается еще одна важная тенденция, наметившаяся при моделировании банковского дела, – отображение в модели роли государственного регулирования. Государство и банк могут рассматриваться как партнеры по взаимовыгодному сотрудничеству в области финансов. Так, государство может выступать гарантом по вкладам и депозитам, обеспечивая тем самым статус наибольшего благоприятствования, и т.д. Если подобного рода деятельность имеет место, она может быть отображена в рассмотренных моделях специальным образом: параллельным переносом вверх функции привлечения депозитов; учетом в портфеле активов льготных кредитов, государственных компенсаций и т.д.

Полные модели банковской деятельности

Если частные модели позволяют проанализировать отдельные аспекты деятельности банковской фирмы (сконцентрировать внимание либо на выборе структуры активов, либо на управлении обязательствами), то в полных моделях используется комплексный подход. По мнению Е.Балтенспергера, полная модель должна обосновывать решения: 1) об активах и обязательствах банка (и их взаимодействии); 2) о размерах банковского капитала. В работе приводится описание структуры полной модели Балтенспергера, позволяющей определить такое соотношение активов и пассивов, которое обеспечивает максимум прибыли банка.

Большой вклад в теорию банковской фирмы сделал К.Сили, который построил квазиполную модель банка путем интеграции описанных выше двух частных направлений моделирования, однако вопросы банковского капитала остались при этом за пределами модели. Основные результаты, полученные Сили, могут быть сформулированы следующим образом.

1. Принимаемые банком решения определяются одновременно издержками, ликвидностью и риском.

2. Стремление избежать риска зависит от условий ликвидности и издержек.

3. Процессы принятия решения не могут быть адекватно описаны только на основе портфельного подхода, так как при этом не рассматриваются ресурсные затраты и поведение, связанное с установлением депозитных ставок. Эти процессы могут быть интерпретированы исключительно с помощью полных моделей банковской фирмы.

Структура модели Сили и ее основные гипотезы состоят в следующем:

• депозитные предложения Dep рассматриваются как функция ставки по депозитам r^п и элемента случайности ξ^п. Таким образом, неопределенность включена в модель вводом случайных депозитных предложений:

Dep = f (ξ^п, r^п); (6.4)

• основное балансовое ограничение определяется равенством ссуд L и депозитных предложений Dep; при этом в балансе участвует составная переменная Z, характеризующая ликвидные средства и принимающая значения Z > 0 или Z < 0 в соответствии с разностью между объемами заимствования и кредитования на рынке краткосрочных капиталов:

L = Dep + Z, (6.5)

где

Z =

• доходы банковской фирмы D определяются как сумма доходов от ссуд D₁ и ссуд «ликвидности» D₂ = Z⁺ (если Z > 0), при этом доходы от ссуд определяются как произведение ставки процента по ним r^a на размер ссуды L, а r^a считается функцией элемента случайности ξ^п:

D = D₁ + D₂, (6.6)

D₁ = r^a · L, (6.7)

D₂ = Z⁺, (6.8)

r^a = φ(ξ^п), (6.9)

• процентные издержки С состоят из издержек по выплате процентов по депозитам С₁ и обеспечению «ликвидности» С₂ = Z^- (при Z ≤ 0):

С = С₁ + С₂, (6.10)

С₁ = r^п · Dep, (6.11)

С₂ = Z^-; (6.12)

• накладные расходы О включают два компонента, представляющие издержки по обслуживанию депозитов и ссуд:

О = η^п · Dep + η^a · L (6.13)

• итоговое уравнение банковской прибыли Пр (за вычетом налогов) имеет вид:

Пр = D – C – O, (6.14)

или

Пр = D₁ + D₂ – C₁ – C₂ – O,

Пр = r^a · L + Z⁺ – (r^п · Dep + Z^- + η^п · Dep + η^a · L).

С помощью модели Сили находится множество сбалансированных решений r^п, L, Z⁺ и Z^-, удовлетворяющих уравнению (6.14). Таким образом определяются портфель кредитов L, депозитная ставка r^п и ликвидная позиция банка.

Модель Сили содержит также функцию риска, которая является возрастающей при увеличении объема ссуд L. Интервал изменения процентных ставок r^п при поведении, минимизирующем риск, шире, чем то же интервал при поведении, нейтральном к риску.

В соответствии с принятыми предположениями банковская фирма рассматривается как действующее предприятие. Поэтому собственный капитал отображен в модели неявно, через прибыльность и ликвидность, которые по сути и определяют его размер.

Другим примером разработки полной модели банковской фирмы служит исследование отечественных ученых по моделированию деятельности коммерческого банка в условиях переходного периода. Данная модель удовлетворяет перечисленным выше формальным требованиям, предъявляемым к полным моделям, т.е. содержит соотношения, характеризующие процесс формирования пассивов и структуру активов, а также изменения, происходящие с собственным капиталом банка. В отличие от модели Сили рассматриваемая модель – динамическая, основанная на принципе положительной обратной связи между текущими результатами деятельности банка и его собственным капиталом (ресурсами) следующего временного интервала. Такого рода положительные обратные связи являются концептуальной основой построения многих динамических моделей, описывающих развитие микроэкономических объектов различной природы и рассматриваемых теорией фирмы.

Еще одной отличительной особенностью модели является ее ориентация на актуальные для переходного периода проблемы выживания коммерческих банков. Это обусловливает включение в нее специального блока расчетных показателей рентабельности и ликвидности, на основе которых методом линейной свертки конструируется интегральный показатель выживаемости банка. Расчет показателей ликвидности и рентабельности осуществляется с использованием отечественной методики, применяемой для составления рейтинга банков в условиях переходного периода.

Вариация параметров внешней среды, в частности ставок по кредитам и депозитам, позволяет косвенным путем (через статистические испытания) изучить последствия складывающейся рыночной конъюнктуры для развития банка. Таким образом, аналитическая зависимость депозитных и кредитных предложений в модели отсутствует, но может быть выявлена экспериментально.

К числу основных соотношений этой модели относятся следующие:

1. Уравнение собственного капитала

SK_t = UF_t + OF_t (6.15)

где t – год рассматриваемого периода;

SK_t – собственный капитал;

UF_t – уставной фонд;

OF_t – фонды банка.

2. Уравнения динамики депозитов. Банк принимает депозиты в объеме, зависящем от величины собственного капитала, стремясь сохранить сложившееся соотношение между собственным и привлеченным капиталом. Рассматриваются три вида депозитов: обязательства до востребования OV_t, межбанковские кредиты MB_t, прочие вклады и депозиты VD_t:

OV_t = OV_{t – 1} + æ₁ ·ΔSK_t, (6.16)

MB_t = MB_{t – 1} + æ₂ ·ΔSK_t, (6.17)

VD_t = VD_{t – 1} + æ₃ ·ΔSK_t, (6.18)

æ₁, æ₂, æ₃ ≥ 0,

æ₁ + æ₂ + æ₃ = 1.

Величина ΔSK_t представляет собой прирост собственного капитала за год и определяется суммой нетто-прибыли банка NP_{t – 1} (т.е. ΔSK_t = NP_{t – 1}); æ₁, æ₂, æ₃ – доли распределения прибыли.

3. Уравнения динамики активов. Рассматриваются ликвидные LA_t и неликвидные SNA_t (средне- и низколиквидные) активы:

LA_t = LA_{t – 1} + æ₁ ·ΔSK_t, (6.19)

SNA_t = SNA_{t – 1} + (æ₂ + æ₃) ·ΔSK_t, (6.20)

Банк выбирает такую стратегию использования привлеченных средств, чтобы не ухудшить свою ликвидность: прирост ликвидных активов соответствует приросту обязательств до востребования, а прирост средне- и низколиквидных активов определяется приростом остальных депозитных средств. В результате пассивы и активы банка взаимосвязаны.

4. Основное уравнение баланса банка

SK_t + OV_t + VD_t + MB_t = LA_t + SNA_t . (6.21)

5. Уравнение расчета прибыли банка. Проводят расчет общего дохода SD_t за вычетом издержек ZB_t; после вычета налогов Tax_t образуется нетто-прибыль NP_t . Для расчета суммарного дохода исчисляется банковская маржа на основе депозитных и кредитных ставок процента и . При этом учитывается структура активов: выделяются работающие активы и резервы, отчисленные в Банк России в порядке обязательных взносов; считается, что среди работающих активов наиболее высокие ставки процента имеют средне- и низколиквидные активы (первый этап переходного периода характеризуется отсутствием ГКО); учитываются индекс инфляции Inf и риск невозврата кредитов (путем введения коэффициентов θ_j, характеризующих долю возвращаемых кредитов в общей сумме соответствующего актива).

SD_t = F , (6.22)

NP_t = SD_t – ZB_t – Tax_t, (6.23)

где F – функция общего дохода от рассматриваемых переменных;

ψ₁ – функция, характеризующая структуру активов и пассивов.

Интегральный показатель выживаемого банка WI_t рассчитывается как взвешенная сумма показателей относительной рентабельности Rent_t и относительной ликвидности Л_t:

WI_t = λ₁ · Rent_t + λ₂ · Л_t, (6.24)

где λ₁ ≥ 0, λ₂ ≥ 0, λ₁ + λ₂ = 1.

Соотношения (6.15) – (6.24) описывают главные аспекты рассматриваемой модели и позволяют выявить следующие возможные направления ее совершенствования: а) учет зависимости величины привлекаемых средств от факторов конкурентной среды, в

Действительно, из условия (Т10) получаем

.

Отсюда

,

или

Таким образом,

4. Область прямой, для которой соответствует значениям

Это следует из аналогичных рассуждений с учетом решения системы

Итак, сопоставление значений индексов и осуществляется на основе сравнительного анализа взаимного расположения двух прямых - биссектрисы и прямой . Участок прямой, лежащий выше биссектрисы, соответствует доминированию индекса депозитных ставок ( ) в условиях возрастающей ди­намики (); участок прямой под биссектрисой отвечает доми­нированию индекса кредитных ставок ( ) и убывающей дина­мике ( < 1) - см. рис. 6.2.

Проиллюстрируем доказанное следующими численными примерами.

Дано: постоянный спред

1. Пусть (возрастание ставок процента).

Найдем область определения (Т 11):

Из (Т 12) следует, что

Таким образом, .

2. Пусть = 0,8 (убывание ставок процента).

Область определения (Т 11 ):

Из (Т 12) следует, что

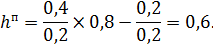Таким образом, .

Итак, доказано, что в условиях постоянного спреда при возрас­тании ставок процента депозитные ставки изменяются быстрее кредитных; при убывании ставок процента кредитные ставки, на­оборот, изменяются быстрее депозитных.

Так как целый ряд российских коммерческих банков имеет дело со сбережениями населения и является своего рода разновиднос­тью ссудо-сберегательных институтов, рассмотрим полученные из теорем выводы применительно к данному классу объектов, функ­ционирующих в условиях снижения уровня инфляции.

Этот случай соответствует следующим знакам переменных: и Для него выполняются результаты, полученные по теореме 1 (о негативном гэпе), а также справедливы соответ­ствующие частные случаи теоремы 2:

1. Чем крупнее банк, тем больший негативный гэп может быть реализован.

2. При меньшем изменении ставки процента можно реализовать больший негативный гэп.

3. При постоянном спреде = и постоянных активах величина предельного негативного гэпа об­ратно пропорциональна ставке процента.

Действительно, обозначив и преобразовав (Т4), имеем

4. Чем больше негативный гэп, тем (при прочих равных услови­ях) меньше процентный доход (так как в выражении (ТЗ) при сни­жении ставки процента всегда ).

5. Если негативный гэл постоянен (структура баланса банка стабильна) и определен в области его возможных значений, то в условиях снижения ставки процента динамика процентного дохо­да характеризуется возрастанием с темпом (см. соотношение (Т3)).

6. В условиях растущей инфляции негативный гэп создает наи­менее благоприятную ситуацию для банка (так как при в соотношении (Т2) лишь одно из трех слагаемых остается положи­тельным, что существенно уменьшает доход). Во время инфляции такая ситуация явилась одной из причин серии массовых банкротств ссудо-сберегательных институтов, имеющих негативный гэп [162].

Подводя итоги выполненного анализа, можно привести следу­ющее образное сравнение, характеризующее роль гэпа в управле­нии банковской деятельностью. Гэп можно уподобить парусу, ори­ентация которого по ветру рыночной конъюнктуры (в соответствии с изменением ставки процента) позволяет судну (банку) без помо­щи мотора и весел (без изменения величины и структуры пассивов и активов) двигаться в направлении, обеспечивающем увеличение доходов. Причем чем крупнее корабль (активы банка), тем больше должен быть и парус (гэп); однако его увеличение и позиция отно­сительно ветра определенным образом ограничены как мореход­ными характеристиками, так и опасностью оверкиля (отрицатель­ных процентных доходов).

С точки зрения процессов взаимодействия банков и объектов реального сектора экономики управление гэпом может оказать дво­якое воздействие: при выборе негативного гэпа создаются предпо­сылки для усиления взаимодействия с вкладчиками (юридически­ми и физическими лицами); при позитивном гэпе - с заемщиками, а также возникают условия для активизации процессов инвестиро­вания и кредитования.

Задача управления ставкой процента в условиях инфляционного и кредитного рисков

При определении ставки процента важным фактором является учет в ней различных рисков (инфляционного, невозврата кредита и т. д.). Эти вопросы частично изучались в гл. 3 (разд. 3.4); при этом было показано, что уровень процентной ставки с учетом рис­ков может быть определен по следующей формуле:

где - реальная ставка или премия за отказ от потребления; х*- ­величина ожидаемой (прогнозируемой) инфляции; - надбавка (премия) за риск непогашения обязательства; - надбавка (пре­мия) за процентный риск (за неожиданную инфляцию). Таким об­разом, величина свободной от риска ставки процента имеет вид

.

Задача управления ею состоит в том, чтобы, с одной стороны, правильно оценить параметры , х* , и и включить их в размер общей рыночной ставки процента , а с другой - согласовать полу­ченную величину с требованиями спроса и предложения на рынке денег, т. е. учесть интересы различных экономических агентов.

Как уже указывалось, неправильная оценка этих параметров приводит к потерям дохода, которые в зависимости от условий про­ведения операции (сделки) могут возникнуть как у кредитора, так и у заемщика. При этом одна из сторон всегда получает дополни­тельный доход, равный сумме недополученного дохода контраген­та, что было иллюстрировано схемой, представленной на рис. 3.3. Для банка, по сути постоянно находящегося и в роли кредитора, и в роли заемщика, правильное определение ставок процента - важ­нейшее условие прибыльной деятельности.

Анализ формул свидетельствует о том, что могут быть рассмот­рены две ситуации.

1. Риск непогашения обязательств равен нулю ( = 0); при этом , где - суммарная надбавка за ожидаемый и неожиданный рост инфляции. Данная ситуация была достаточно полно рассмотрена в гл. 3, где исследовалась задача определения величины и последствий, возникающих при ее недооценке или переоценке (эффект Фишера).

2. Риск неожиданной инфляции равен нулю ( = 0); при этом где - реальная ставка процента, скорректиро­ванная с учетом прогнозируемой (учитываемой, наблюдаемой) ин­фляции, т. е. ставка процента, свободная от риска. В этом случае задача состоит в оценке параметра , представляющего собой над­бавку за кредитный риск (риск невозврата кредитов).

Рассмотрим основные факторы, влияющие на величину .

Кредитный риск - это вероятность неисполнения заемщиком обязательств по ранее полученному кредиту. Если обозначить эту вероятность , то взаимосвязь риска и дохода (при отсутствии, согласно предположению, других видов риска) может быть представлена следующей формулой:

где - вероятность возврата кредита; - безрисковая став­ка процента; - фактическая ставка процента с учетом данного (кредитного) вида риска (удельный доход с единицы вложения).

Формула выражает фундаментальное правило банковского дела: "риск требует компенсации" и может быть интерпретирована как возможность уменьшения процентной ставки для надежного кли­ента, репутация которого позволяет дать высокую оценку вероят­ности возврата ссуды, и, наоборот, как необходимость повышения ставки процента при высокой вероятности невозврата кредита [162].

Так, если имеется полная уверенность в возврате ссуды ( , то , т. е. будет использована безрисковая ставка процента; если заранее известно, что заемщик почти наверняка не вернет долг , то величина не поддается определению (риск кредитора компенсировать невозможно):

.

Разность представляет собой премию за риск невозврата кредита, которую получает банк, а оплачивает заемщик. Преобра­зуем формулу для определения кредитного риска следующим об­разом:

или

Отсюда имеем

Таким образом, премия р за риск невозврата кредита пропорци­ональна произведению величины кредитного риска и ставки про­цента .

В условиях переходного периода и параллельного хождения в российской экономике двух валют кредитные риски должны быть рассмотрены с учетом привязки их к конкретной валюте, используемой при осуществлении кредитной операции. В частности, фор­мула, связывающая риск и величину ставки процента, может быть использована также для интерпретации расхождения эффективно­сти процентных ставок для счетов с разной валютой. Так как обес­ценение вложений правомерно рассматривать как особую форму невозврата части кредита, то более надежная валюта (с меньшим темпом инфляции и обеспечивающая более полный возврат реаль­ной суммы) будет иметь относительно меньшую ставку процента, и наоборот. Ясно, что чем значительнее различие в степени дове­рия к функционирующим валютам, тем больше расхождение и в соответствующих им ставках процентов (заметим, что для выпол­нения сравнения ставок процента их приводят к единому измери­телю с учетом сложившегося паритета валют). Соответственно и величина премии за риск невозврата кредита, включаемая в ставку процентов, будет различна.

Итак, управление процентным риском в данной ситуации со­стоит в том, чтобы на основе наиболее точной оценки вероятности невозврата кредита определить величину надбавки (премии) , включаемой в размер процентной ставки:

В случае двухвалютной системы эта премия рассчитывается по каждой валюте автономно с учетом соответствующего риска.

Следует отметить, что составляющая процентной ставки, учи­тывающая кредитный риск, не всегда покрывает риски невозврата кредитов мелких и средних банков в силу малости их кредитных портфелей и, как следствие, незначительности общей суммы ком­пенсации, получаемой по этому виду риска.

Задача управления кредитным риском

Ее можно считать составной частью задачи управления процен­тным риском или предварительной фазой рассмотренной ранее, в гл. 5, задачи планирования величины удельного веса просрочен­ных (а при необходимости - и проблемных) кредитов (активов). Однако ввиду ее важности она часто рассматривается как самосто­ятельная проблема.

Очевидно, что банки и взаимодействующие с ними предприя­тия заинтересованы в снижении вероятности не возврата кредита и величины надбавки р: первые - поскольку это улучшает их финансово-экономические показатели и увеличивает спрос на кре­диты, вторые - потому что кредиты становятся более доступными и предприятиям не приходится покрывать оплатой процентов "чу­жие долги".

Для того чтобы обеспечить снижение величин и р , банкам рекомендуется применять экспресс-методы селекции клиентов по их финансовой благонадежности. Для рынка кредитов характерна асимметричность информации: свое экономическое состояние кли­ент знает лучше, чем банк, что дает ему преимущество при заклю­чении договора о кредите. В этой ситуации банку чрезвычайно важно иметь эффективные и удобные методы оценки заемщика. Суще­ствует целый ряд таких методов, которые позволяют:

1) классифи­цировать предприятия по их кредитоспособности на группы [22], производить оценку инвестиционных проектов, под которые бе­рется кредит [129], осуществлять аудит предприятия [199] и т. д. В данной работе приводятся два достаточно простых метода оценки клиентов, не требующих ни значительного времени, ни затрат. Ус­пешно пройдя сквозь "грубое сито" таких методов, в дальнейшем эти клиенты могут быть изучены с помощью более тонких тестов.

В частности, на Западе в качестве инструмента, играющего роль подобного теста широкое распространение получила модель CART (Classification and Regression Trees). Математический аппарат, при­меняемый в модели (регрессионные методы), позволяет получать бинарные классификационные деревья, анализ которых осуществ­ляется на основе алгоритма, использующего принцип дихотомии [222]. На рис. 6.3 представлено дерево классификации, на котором в прямоугольниках заключены четыре показателя - индикаторы состояния фирмы а в кружках отмечено условие классификации относительно заданных моделью CART значений этих показателей Двумя кружками и значком Nb помечены фирмы-небанкроты, т. е. благонадежные заемщики. В соответствии с моделью CART это такие фирмы, для которых вы­полняются два типа условий:

1)

2)

Исследования, проведенные для американских банков по модели CART, дали следующие критериальные значения этих показателей:

= 0,1309; =0,1453; =0,25; =0,6975.

Точность модели CART составляла при этом 90% [222].

Аналогичные исследования применимы и в условиях российской экономики (с учетом повышенных рисков предприятий [93, 188]); отметим, что значения переменных (i = 1-4) требуют предварительного определения с помощью статистических методов об­работки эмпирических данных.

Nb – благонадёжные заёмщики, не банкроты

Nb

Nb

Рис. 6.3. Классификационное дерево модели CART для выявления фирм-банкротов

Еще один метод определения благонадежных заемщиков носит название Z-анализа, в основе которого лежит Z-модель Альтмана [202, 203]. В Z-модели используются статистические методы (дискриминантный анализ), целью которого является отбор сово­купности показателей, наилучшим образом классифицирующих объекты (фирмы) по двум группам - банкроты и небанкроты. В базовой Z-модели содержатся пять таких показателей:

Уравнение оценки имеет вид

где величины получены посредством обработки статистических данных.

Правило классификации Z-модели таковы:

1. если , фирму относят к группе банкротов;

2. если , - к группе благонадежных заемщиков.

При этом интервал при (или окрестность критериального значения ) считается "зо-ной неве­дения" или зоной возможных ошибок.

В дальнейших исследованиях модель была модифицирована: в ее состав вошло семь критериальных показателей [203].

Рассмотрим еще один фактор, влияющий на кредитный риск, - величину кредитной ставки процента.

В проведенном выше анализе рассматривалась зависимость ре­альной кредитной ставки процента от кредитного риска. Но суще­ствует и обратная зависимость: чем выше кредитная ставка, тем больше риск невозврата кредита. Это означает, что кредитный риск возрастает как с ростом инфляционного риска, так и при необос­нованном завышении премий за различные риски, вызванном их переоценкой (иными словами, при увеличении слагаемых , р и т). Рассмотрим последствия завышения кредитной ставки процента более подробно на следующем примере.

Пусть на рынке кредитов имеются два типа заемщиков: благо­надежные, возвращающие кредит, и неблагонадежные, использу­ющие средства для различных рискованных операций (финансо­вых авантюр) и не предполагающие возвращения кредита. Вторая группа заемщиков создает дополнительный (ложный) спрос на кре­диты LD (lie deтand), сдвигая истинную кривую спроса TD (truth deтand) параллельно вверх (рис. 6.4). В связи с этим повышается и цена кредита как равновесная точка спроса LD и предложения Sиp (sиpply). Пусть известна средняя эффективность инвестицион­ных вложений (например, для того сектора народного хозяйства, где специализируется рассматриваемая банковская фирма). Тогда при доля добросовестных заемщиков в общем числе пре­тендентов будет невелика: среди них будут только те немногие, чья эффективность существенно выше средней; зато очень высокой окажется доля неблагонадежных клиентов, готовых взять кредит любой ценой. В том случае если банк снижает ставку процента (например, исключая полностью или частично кредитный риск р) до уровня , доля благонадежных клиентов возрастает, а риск невозврата кредита уменьшается.

Sup

LD

TD LD

Sup

TD

О

Рис. 6.4 . Управление ставкой процента k с учетом минимизации кредитного риска:

LD – ложный спрос, TD – истинный спрос, Sup – предложение

Очевидно, что банк выберет ставку (или , где - ­малая величина), которая, с одной стороны, обеспечивает доста­точную прибыль, а с другой - соответствует относительно неболь­шой доле неблагонадежных заемщиков; точка О будет характери­зовать состояние реального (истинного) равновесия, определяемого истинным спросом TD и предложением Sиp.

Несмотря на упрощенный характер приведенной здесь концеп­туальной модели равновесия, учитывающей риск невозврата кре­дита*, она представляется важной для понимания процессов, про­исходящих в сфере современного российского банковского бизнеса. В частности, значительное распространение получило явление умышленного невозврата кредита, мешающее развитию банков-

* Более строгая постановка данной задачи приводится в работе [6].

Ского дела и являющееся в ряде случаев причиной банкротств кредитных организаций.

Модель позволяет сделать следующие выводы:

1) Риск невозврата кредита не может быть устранён полностью;

2) Рассматриваемый риск может быть уменьшен за счёт снижения доли неблагонадёжных заёмщиков в общем числе клиентов;

3) уменьшение риска достигается снижением ставки банковского процента до (или ниже) уровня средней эффективности вложений. В результате банк уменьшает не только доходность, но и кредитный риск, как бы перераспределяя его между благонадёжными заёмщиками.

Полученные результаты соответствуют практике банковского дела: солидные банки, работающие с надёжными клиентами, характеризуются относительно невысокими ставками процента, учитывающими снижение фактического риска невозврата кредитов.

Задача управления ликвидностью.

Управление банковской ликвидностью – это процесс создания средств, для того, чтобы иметь возможность оплатить договорные обязательства по приемлемым ценам и в любое время.

С точки зрения банковского баланса выделяются две основные функции ликвидности: удовлетворение спроса на кредиты и (или) пожеланий вкладчиков изъять депозиты. Так как банки могут планировать ожидаемые изъятия и кредиты, то именно неожиданные изменения этих переменных создают риск ликвидности. Поэтому банкам необходим амортизатор в виде резервов ликвидности.

Различают внутренние и внешние источники накопления банковской ликвидности: 1) внутренние – превращение активов в наличность и создание резервов (корреспондентские счета и касса); 2) внешние – покупка ликвидных активов (ценных бумаг, депозитных сертификатов и т.д.)

Чтобы обеспечить необходимую ликвидность, банки должны создавать резервы (накапливать, как правило, низкодоходные ликвидные активы, наличность и т.д.), что снижает доходность их деятельности. Таким образом, возникает альтернатива: максимум доходности и большой риск ликвидности или снижение доходности при повышении ликвидности. Решение этой оптимизационной задачи с двумя конкурирующими критериями может быть найдено методами линейного программирования. В ней один из критериев (ликвидность) представлен в виде ограничения, а другой (доходность) является целевой функцией.

Пусть баланс банка имеет вид:

L+A^Д = OV + Dep +SK,

Где L – ликвидные активы (ценные бумаги, наличность);

A^Д - доходные (работающие) активы;

OV – обязательства до востребования;

Dep - срочные депозиты;

SK – собственный капитал.

Чистый процентный доход D^пр определяется соотношением:

D^пр = [r₁*L +r₂*A^Д – (r₃*OV+r₄*Dep)] → max,

Где r₁, r₂ - ставки процента по ликвидным и доходным активам соответственно; r₃, r₄ - ставки процента по депозитам ( до востребования и срочным).

Ликвидное ограничение (как правило, в соответствии с нормативными положениями, устанавливаемыми органами, регулирующими банковскую деятельность) определяется в долях всех активов по нормативу l:

L*(L+A^Д)≤L

Ограничения на кредиты представляет собой неравенство

А^Д ≤А^Д0

Где А^Д0 - заранее заданная величина.

Обозначим SS = OV + Dep + SK, причём три последние величины в данной задаче известны; целевую функцию упростим, оставив лишь два первых слагаемых и исключив константы. После проведения необходимых преобразований получим следующую систему соотношений, определяющих модель управления ликвидностью:

Отметим, что данная постановка задачи исходит из классического положения рыночной экономики о конкурирующих критериях дохода и ликвидности. Однако квазирыночная экономика переходного периода внесла некоторые коррективы и в эту сферу. Дело в том, что введённые государством в 1996 году и существовавшие до августа 1998 года ценные бумаги (ГКО и т.д.) обладали большей ликвидностью и в то же время являлись наиболее доходными. Пренебрегать данным фактом, как досадной мелочью, не вписывающейся в классическую теорию, нельзя: до августовского кризиса 1998 года указанные ценные бумаги были весьма привлекательными и составляли значительную часть работающих активов многих российских банков, причём лидером среди них был Сбербанк России, контролировавший в некоторые периода более 30% рынка этих ценных бумаг. С точки зрения задачи линейного программирования (1) – (5) это означает, что в рассматриваемой ситуации лимитирующими ограничениями могут стать (1) и (2), а ограничение (3), описывающее прочие работающие активы, по всей вероятности, в данной ситуации лимитирующим не будет и поэтому может быть опущено.

Заметим, что в настоящее время по мере восстановления цивилизационного рынка и стабилизации экономики наметилась тенденция к снижению уровня доходности государственных ценных бумаг, но и повышения риска их ликвидности.

торый зависит как от рациональной селекции заемщиков, так и от гарантий государства. В результате осуществляется обоснованный выбор необходимых значений слагаемых ставки процента: k = r + x^* + p + m; (^* В данном случае p(t) – кредитный риск депозитора (вкладчика), определяющийся категорией надежности банка.

3) оценку риска ликвидности (с учетом того, что ликвидность и доходность являются конкурирующими показателями);

4) анализ основных показателей банковской доходности (процентного и общего дохода, процентной банковской маржи и т.д.);

5) учет возможной государственной поддержки и ее влияния на показатели доходности, объема привлеченных депозитов, размер кредитной ставки процента и т.д.

6.3 Общая математическая постановка задачи оптимизации развития банка с учетом его взаимодействия с промышленностью

Цель данного раздела состоит в формулировании и анализе концептуальной модели функционирования банка, которая в агрегированной форме описывает основные зависимости, характеризующие динамику его развития и условия взаимодействия с промышленным сектором экономики в переходный период. Модель основана на концепции равновесия спроса и предложения на рынке денег позволяет исследовать такие динамические характеристики системы (внутренние управляющие воздействия и параметры внешней среды), которые обеспечивают достижение равновесия, интерпретируемого как наиболее благоприятное состояние процесса взаимодействия банка и реального сектора экономики.

При этом будем исходить из следующих положений.

1. исходные посылки:

а) рассматривается стадия переходного периода, характеризующаяся снижением темпов инфляции и некоторой стабилизацией производства (наблюдается снижение темпов падения выпусков продукции по ряду отраслей, а по другим отраслям – небольшое повышение объемов производства). В приведенной выше формуле, характеризующей депозитную ставку процента, введем переменную времени t: k(t) = r(t) +x(t) + p(t) и проанализируем основные тенденции изменения слагаемых. Если премия за отказ от потребления не изменяется (r(t) = const), а х (t) и p (t) являются монотонно убывающими функциями времени (ввиду снижения темпов инфляции и уменьшения кредитного риска депозитора), функция k(t) также будет убывать монотонно (причем быстрее, чем функция снижения инфляции);

б) предположим, что на данном этапе анализа (в целях его упрощения) спред s(t) является величиной постоянной: s(t) = s = const. Тогда динамика кредитной ставки k^a(t) тоже может быть представлена как монотонно убывающая функция времени t, располагающаяся параллельно на функцией k(t), так как k^a(t) = k(t) + s;

в) для анализа используем равновесный подход [65] и рассмотрим характер зависимостей предложения Sup(k) и спроса Dem(k^a) на денежный ресурс в зависимости от величины депозитной и кредитной ставки процента k и k^a соответственно. Опять же для простоты на данном этапе будем рассматривать один вид вложений как на рынке депозитов, так и на рынке кредитов. Очевидно, что Sup(k) является возрастающей функцией от k, а Dem(k^a) – монотонно убывающей от k^a. Вид этих зависимостей изображен на рис. 6.5а и 6.5б.

Здесь Sup₀ характеризует предельную величину сбережений, которые могут быть отложены на депозиты; k₀ – минимальную ставку процента, которая не только компенсирует инфляцию и риски, но и обеспечивает некоторую среднеотраслевую (а для условий переходного периода – минимально возможную) рентабельность Rent^*, т.е. k₀ ≥ Rent^*; в противном случае инвестиции могут быть вложены в наиболее рентабельные сферы производства в соответствии с принципом диверсификации вложений (рис. 6.5а).

Рис.6.5. Зависимости предложения Sup(k) и спроса Dem(k^a)

Величина Dem₀ на рис.6.5б характеризует максимальную емкость инвестиционного рынка, соответствующую минимально возможной кредитной ставке процента , т.е. Dem_{0 =} Dem( ). Параметр , отвечающий максимальному спросу на кредиты, является такой величиной кредитной ставки, при которой банковская маржа стремится к нулю: s → 0, → = Rent^*.

Минимальный спрос на кредиты соответствует максимальной ставке процента ; при этом = + s^*, где s^* - максимально возможная маржа банка. Величина s^* определяется условием минимальной привлекательности вложений для инвестора (предприятия); т.е. предприятие, выплатив долговые обязательства 9процнты), должно обеспечить себе средний (от альтернативных вложений) доход Rent ≥ Rent^* + s + .

Заметим, что кривая Dem( ) может быть получена путем параллельного переноса влево кривой, изображенной на графике рис.6.5а (с учетом того, что соотношение между осями графиков отражается равенством k^a = k +s). Поместив зависимости Sup(k) и Dem(k^a) в единую систему координат, построим график, показанный на рис.6.6. Здесь О – точка равновесия, а k - соответствующая ей равновесная ставка процента.

2. Современное положение типичного банка может быть охарактеризовано как неравновесное, причем область неравновесия характеризуется недоступностью кредитов для предприятия реального сектора экономики. Как следует из графика рис.6.6, в настоящее время банковская система находится в области высоких значений параметра ( области ε) справа от точки равновесия О. Это означает, что при > k банки испытывают затруднение при вложении аккумулированных средств и часть из них не используется.

Рис.6.6. Соотношение предложения Sup(k) и спроса Dem(k).

Что касается участка области значений < k , то в этой ситуации банк не может осуществить эффективное привлечение средств, а следовательно, и обеспечить собственное развитие. Т.е. несет альтернативные убытки. Очевидно, что точка равновесия О является наиболее привлекательным состоянием его развития, но пока не может быть достигнута.

Обеспечение равновесия только за счет методов внутрибанковского управления затруднено. Как уже указывалось, возможности снижения параметра r уменьшают привлекательность хранения денег в банке (в соответствии с предложением ликвидности, по Дж.М. Кейнсу, хозяйственные агенты предпочтут наличность); искусственное занижение х, согласно эффекту Фишера, обусловит потери банковской прибыли, а уменьшение значения составляющей p увеличит убытки в связи с невозвратом кредита.

Вариант с уменьшением только кредитной ставки при сохранении процента по депозиту (что сопровождается уменьшением спреда линия Dem^’(k) на рис.6.6), конечно же, сокращает разрыв между величинами спроса и предложения. Но не привлекателен для банка, так как приводит к уменьшению его процентного дохода. (Точнее, уменьшение спреда может оказаться привлекательным для банка лишь до тех пор, пока оно обеспечивает снижение кредитного риска. Как это было показано ранее.)

Таким образом, для рассматриваемой стадии переходного периода указанная неравновесная ситуация является достаточно устойчивой с точки зрения ограниченности возможностей внутрибанковского управления. Для достижения равновесия необходимо изменение параметров внешней среды.

3. Рассмотрим изменение функций Dem(k) и Sup(k) во времени, добавив в анализ параметр времени t.

Так как в соответствии с пунктом б исходных посылок k(t) - монотонно убывающая зависимость, то функция φ[Dem(k),k(t)], является возрастающей, а ψ[Sup(k),k(t)] – убывающей во времени.

Таким образом, движение к равновесной точке и сходимость процесса обеспечивается в данной ситуации не колебанием значений спроса и предложения вокруг точки О (как в паутинообразной модели [4]), а последовательным движением вдоль кривых Dem(k) и Sup(k), обусловленным изменением параметров внешней среды х и p (см. стрелки на рис.6.6). Очевидно, что при принятых предположениях равновесие может быть достигнуто. Это и означает созревание предпосылок для активного инвестирования в реальный сектор.

4. Исследуем более сложную ситуацию наличия нескольких видов депозитных и кредитных вложений в условиях возможных изменений параметров r(t) и s(t) как результата внутрибанковского управления.

Задача сводится к необходимости выбора наиболее эффективных путей движения к многомерному равновесному состоянию в условиях существования целого набора кривых Sup(k) и спроса Dem(k) посредством соответствующего изменения r(t) и s(t), являющихся в этом случае параметрами управления.

5. Для оптимального описания изложенной выше задачи используем оптимальный подход.

Формулировка оптимальной модели развития банка

Оптимальная задача формирования банковской стратегии может быть представлена в следующем виде:

(6.44)

(6.45)

(6.46)

(6.47)

(6.48)

(6.49)

opt {C = f [ (6.50)

В качестве целевой функции могут быть рассмотрены:

а) максимум процентного дохода:

max ={C = } (6.50a)

б) минимум суммы квадратов отклонений от целевой точки , определяющей инвестиционные вложения:

min{C = ²}; (6.50б)

в) максимум взвешенной суммы критериев доходности, банковских резервов и ликвидности:

max{C=λ₁ (6.50в)

где 0 ≤ λ₁ ≤1; 0 ≤ λ₂ ≤ 1; 0 ≤ λ₃ ≤ 1; λ₁ + λ₂ + λ₃ = 1;

г) максимум процентного дохода с учетом риска невозврата кредита:

max{C = (6.50г)

где ( - доля возвращаемых кредитов, зависящая, в частности, от уровня ставки ; 0 ≤ ≤ 1.

6. Интерпретируем модель (6.44-6.50) и поясним содержание сформулированных выражений.

Задача рассматривается в параметрической форме. Параметры управления обозначены символом U с изменяющимся верхним индексом, соответствующим индексу той переменной, которая зависит от данного параметра (т.е. определяют вид переменной). Нижние индексы i и j означают соответственно вид вклада или инвестиций банка. При этом вклады вида i являются нелинейной функцией депозитной ставки , а инвестиционные вложения вида j нелинейно зависят от кредитной ставки (влияющей на спрос клиентов банка на кредиты и инвестиции).

Уравнение (6.44) определяет ограничение по суммарной величине вложения средств на депозитном рынке , которые не могут превышать предельную величину сбережений , размещаемых по прогнозу в депозиты.

Уравнение (6.45) отражает процесс размещения кредитных ресурсов с учетом как привлекаемых пассивов, так и собственного

капитала. При этом неразмещенная в кредиты часть собственного капитала SK, имеющая неликвидную форму (здания, сооружения, оборудование и т.д.), но являющаяся потенциальным резервом увеличения работающих активов , путем направления в них средств, полученных под залог, образует второе слагаемое банковских активов. Так как общая величина размещения кредитных ресурсов не может превышать максимальную емкость инвестиционного рынка , то после перенесения величины SK в правую часть неравенства получаем выражение (6.45). Уравнение (6.46) представляет собой уравнение баланса банка вида П – А + SK ≥ 0 и учитывает нормы обязательного резервировании банка:

• резервы, отчисляемые в Банк России, в зависимости от вида депозитов определяются параметром-нормативом ;

• резервы, создаваемые банком с учетом риска невозврата кредитов, - переменной .

В задачу вводится ограничение на гэп (выполняющее роль стабилизатора кредитно-инвестиционной стратегии), содержащее параметр δ (принимающий в общем случае положительные, нулевые и отрицательные значения) и записываемое в виде (по модулю):

Так как задача рассматривается для ситуации падения темпов инфляции и дл реализации кредитно-инвестиционной стратегии банка целесообразен негативный гэп, приведенное уравнение принимает вид

и записывается в задаче в виде неравенства (6.47). При этом дл простоты полагают, что Wi и Zj являются пассивами и активами, чувствительными к изменению процентной ставки.

Ограничение на ликвидность L (неравенство 6.48) включает параметр-норматив и определяется по аналогии с уравнением, приведенным в разд. 6.2. Неравенства (6.49) являются условиями неотрицательности искомых переменных, образующих банковскую стратегию; соотношение (6.50) представляет собой целевую функцию С, вид которой определяется конкретной постановкой задачи и может быть описан, в частности, уравнениями (6.50а) – (6.50г).

Параметры управления , , , , и изменяются в некотором интервале, который определяется как внешними воздействиями экономической среды для рассматриваемого промежутка времени, так и внутрибанковским управлением (табл. 6.2). Таблица 6.2

Переменные модели

Переменные	Вид управления
	Внутрибанковское управление	Внешняя среда
- депозитная ставка процента	- премия за отказ от потребления	- инфляционный риск
- кредитная ставка процента	– спред	– кредитный риск
- норматив ликвидности	-	- управление центрального органа банковской системы
- нормативы отчислений в резервы	- доля резервирования с учетом риска невозврата кредита (R = 2)	- норматив резервирования ЦБ (R = 1)
- желаемая величина гэпа	Г (X) – величина гэпа	X – общий инфляционный риск

7. Проведем анализ модели и возможных методов ее решения.

Соотношения (6.44) – (6.50г) представляют собой набор вариантов постановки оптимальной задачи, отражающей предложенным способом процентные риски, риски ликвидности и невозврата кредита. Однако возможны и принципиально другие варианты учета рассмотренных рисков, например с использованием аппарата теории вероятностей и математической статистики. Допустимы и такие виды постановки задачи, которые включают другой набор ограничений и критериев. Важным, на наш взгляд, является следующий факт: подобный подход позволяет определить общие направления кредитно-инвестиционной стратегии банка. Так, если в процессе решения задачи выясняется, что в оптимальной точке соотношение (6.44) обращается в строгое равенство, дефицитным является депозитный ресурс и допустимое изменение в рамках депозитно-аккумуляционной и процентно-ценовой стратегий может состоять в увеличении депозитной ставки процента для аккумуляции дополнительных средств. В том случае если в строгое равенство обращается соотношение (6.45), то дефицитным является кредитно-инвестиционный ресурс и стратегия банка может состоять в увеличении кредитной ставки процента.

На примере данной постановки задачи очевидно, что оптимальная модель (6.44) – (6.50) является по сути нелинейной, так как не линейные функции W_i(U_i^W) и Z_j(U_j^Z) входят как в ограничение задачи так и в функционал.

Исследуем характер используемых нелинейных зависимостей и определим тип нелинейной задачи. Анализ реальной информации показывает, что функции W_i(U_i^W) и Z_j(U_j^Z) трудно поддаются формальному описанию в силу влияний на объем вложений и величину размещенных кредитов не только ставки процента, но и целого ряда других факторов (уровень дохода, склонность к отложенному спросу, изменяющаяся доходность в зависимости от альтернативных вложений, экономическое положение отраслей, регионов и предприятий, конкурентные предложения других банков и т.д.) Однако в целом можно считать что зависимость W_i(U_i^W) носит возрастающий характер и выпукла вверх, так в условиях стабилизирующийся экономики и ослабевающего влияния прочих факторов с ростом ставки процента объем по вкладом имеют тенденцию к возрастанию с некоторым насыщением, что и определяет указанный характер его изменения. Функция Z_j(U_j^Z) является убывающей и вогнутой (выпуклой вниз), поскольку при возрастании ставки процента за кредит объем размещаемых ресурсов уменьшается со снижающимся темпом до некоторого минимального уровня [Величина этого уровня зависит от показателя рентабельности заемщика, его благонадежности и т.д., что обсуждалось ранее в разд. 6.2.].Это определяет вид выбранных в задаче (6.44) – (6.50) зависимостей W_i(U_i^W) и Z_j(U_j^Z), изображенных на рис. 7.2 и 7.3 (разд. 7.1). Таким образом, задача (6.44) – (6.50) содержит как выпуклые, так и вогнутые функции и не может быть отнесена к классу задач выпуклого программирования, методы решения которых (наискорейшего спуска, штрафов, возможных направлений, проекции градиента и т.д.) относятся к достаточно эффективным [126] [Задачи выпуклого программирования предполагают максимизацию вогнутой функции на выпуклом множестве (компакте) или минимизацию выпуклой функчии на выпуклом множестве].

Как известно, точное решение подобных нелинейных оптимальных задач оказывается достаточно сложным, поскольку оно обычно требует создание специальных алгоритмов. Заметим, описанная выше задача еще более усложняется, если учесть, что параметры управления функциями зависят от времени t.

В подобных случаях обычно используют приближенные методы решения. В данном разделе предлагается метод декомпозиции сложной задачи на более простые локальные задачи, решение которых определенным образом взаимосвязаны. Он может быть осуществлен, в частности, с применением имитационно-оптимизационного подхода (метода построения имитационных систем), суть которого состоит в следующем.

В задаче (6.44) – (6.50) имеющиеся выпуклые функции W_i(U_i^W) заменяем на конкретные значения, получаемые экспертным путем на основе прогноза динамики привлекаемых денежных ресурсов. В этом случае задача оказывается преобразованной в стандартную задачу выпуклого программирования сепарабельного типа (целевая функция и ограничения представлены в виде сумм вогнутых функций от одной переменной) [126]. Таким образом обеспечивается сочетания имитационного подхода (экспертный прогноз данных) с поиском оптимального решения задачи выпуклого программирования.

8. Рассмотрим более подробно описанный декомпозиционный подход с учетом фактора времени. В качестве примера его реализации авторами рассматривается следующий цикл задач, решаемых для каждого момента времени t.

Задача А Имитационная модель динамики привлекаемых кредитно-инвестиционных ресурсов.

На основе прогноза инфляции и динамики ставки процента (фактор ) определяются возможные значения привлекаемых ресурсов W_i(U_i^W) на рынке депозитов. При этом могут быть рассмотрены как различные сценарии протекания инфляции (фактор _i), так и возможные комбинации внутрибанковских стратегий оп отношению к процентной ставке (фактор r_i). Прогнозируя далее варианты норматива резервной политики Банка России и величину соответствующих резервов R_r(u_r), а также учитывая собственный капитал банка SK, определяем величину кредитно-инвестиционных ресурсов, т. е. объем средств, которые банк может направить на операции инвестирования и кредитования.

Задача В. Оптимальная модель распределения кредитно-инвестиционных ресурсов.

Задавая различные варианты спреда s и прогнозируя величину общего спреда на кредитно-инвестиционных ресурсы, определяем правую часть ресурсного ограничения оптимальной задачи как минимум двух величин:

а) предложение инвестиций и кредитов Sup₀;

б) спроса на инвестиции и кредиты Dem₀.

Оптимальная задача содержит и другие ограничения: на ликвидность, величину гэпа и, возможно, на конкретные виды инвестиций и кредитов; искомые величины – объем распределяемых средств. Целевой функцией может быть любая из описанных выше (формулы (6.50а) – (6.50г)).

Заметим, что поиск решений таких задач даже при разработанных методах достаточно сложен (хотя и принципиально возможен). Поэтому следующим шагом упрощения задачи (который далее и будет сделан) является ее линейная аппроксимация.

Задача С. Имитационная модель расчета основных показателей функционирования банка.

Полученное в задаче В оптимальное решение позволяет рассчитать величину процентного дохода, общих затрат, связанных с банковской деятельностью, общей и чистой (за вычетом налогов) прибыли банка, осуществить распределение прибыли и найти увеличение собственного капитала SK.

Этой задачей заканчивается цикл расчетов и осуществляется переход к задаче А для момента времени t+1. При этом в задачу А поступает информация об увеличении собственного капитала, полученная ранее из задачи С. Таким образом, цикл расчетов замыкается и повторяется далее для каждого временного шага горизонта рассмотрения (см. рис. 6.7).