Тема 3.1. Методи розв’язування систем лінійних рівнянь

Метод простих ітерацій.

Метод Зейделя.

Теорема Кронекера – Капелі (критерій сумісної системи лінійних рівнянь).

Розв’язування систем n-лінійних рівнянь з n-невідомими за формулами Крамера

В результаті вивчення теми студенти повинні:

Знати – алгоритм методу простих ітерацій, методу Зейделя, критерій сумісності СЛАР, формули Крамера розв’язування n-лінійних рівнянь з n-невідомими;

Вміти – розв’язувати рівняння методом простих ітерацій, методом Зейделя, за формулами Крамера для n-лінійних рівнянь з n-невідомими

Завдання:

1. Опрацювати теоретичний матеріал, наведений в методичці, а також скористатись книгою Самарський а.А., Гулин а.В. Численные методы. (папка «Підручники») стор. 82-95

2. Коссак о., Тумашова о., Коссак о. – Методи наближених обчислень: Навчальний посібник, стор. 40-45

3. Вычислительная математика: Учебное пособие для техникумов/ Данилина Н.И., Дубровецкая Н.С., Кваша О.П., Смирнов Г.Л., стор. 98-108

4. Знайти розв’язок системи:

5. Дати відповіді на питання:

1. Яку систему називають системою лінійних алгебраїчних рівнянь?

2. Що називається розв'язком СЛАР?

3. Яка система називається сумісною і несумісною?

4. Яка система називається визначеною і невизначеною?

5. Яка система називається виродженою і невиродженою?

6. Які системи називаються еквівалентними?

7. Яку СЛАР можна розв'язати на ЕОМ?

8. Які методи відносять до наближених (дати означення і перелічити методи)?

9. Пояснити хід методу ітерацій.

10. За допомогою якого алгоритму можна розв’язати систему методом Зейделя?

Метод простих ітерацій.

Розглянемо систему лінійних алгебраїчних рівнянь виду:

                    (1)

Для розв’язання системи (1) методами послідовних наближень необхідно виконати наступні кроки:

1) Кожне рівняння системи розділити на діагональний елемент а_kk, де k=1,2...n, n – кількість рівнянь в системі, і перетворити кожне рівняння системи відносно координат вектора, індекс якого співпадає з номером рівняння:

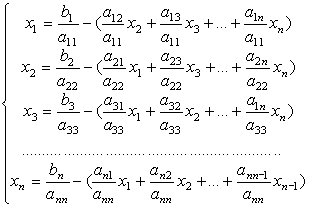          (2)

     2) Нехай , а , де k=1,2…n; i=1,2…n. Тоді система (2) матиме вигляд:

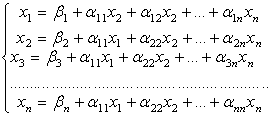               (3)

Така система називається зведеною до нормального вигляду.

     3) Представимо систему (3) в матричному вигляді:

,     (4)

або векторному

.                         (5)

Якщо деяким чином визначити, так званий, вектор початкових значень , який знаходиться в правій частині (5), то можна отримати певні значення вектора .

В якості вектора початкових наближень вибирають:

  вектор, в якого всі координати х_і дорівнюють 0;

  вектор, в якого всі координати х_і дорівнюють 1;

  вектор, координати якого дорівнюють координатам вектора вільних членів ;

  координати вектору вибирають в результаті аналізу особливостей об’єкту дослідження та задачі, яка розв’язується.

4) Якщо вектор початкових наближень підставити в праву частину системи (3.5) або (3.6), то вона прийме вигляд:

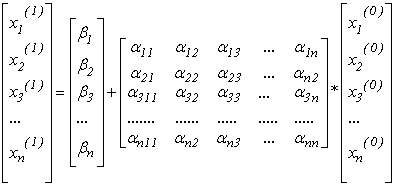aбо ,

легко розв’язується, тому що в правої частині містить всі визначені елементи, і дозволяє отримати розв’язок системи, який називається вектором першого наближення .

5) Перевіряється виконання умови закінчення ітераційного процесу пошуку розв’язку системи (1) виду:

                         (6),

де - задана похибка результатів розв’язання задачі.

Якщо умова (6) не виконується, то підставляється в праву частину (4) або (5) і знаходиться з системи виду:

aбо .

6) Знову перевіряється виконання умови закінчення ітераційного процесу пошуку розв’язку системи (1)

.

Якщо умова не виконується, то підставляється в праву частину (4) і знаходиться з системи виду:

.

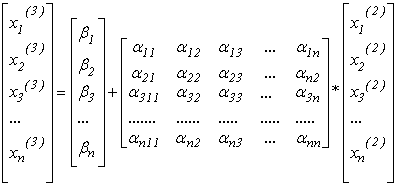і т.д.

7) Етапи 4 та 5 повторюються до тих пір поки на якому-небудь к - ому кроці не виконується умова

.                    (7)

Таким чином, процес пошуку розв’язку системи (1) наближеними методами з заданою похибкою є ітераційним, а умовою виходу з цього процесу є умова (7).