1. Використовуючи метод ітерацій розв’язати систему нелінійних рівнянь з точністю до 0,01.

З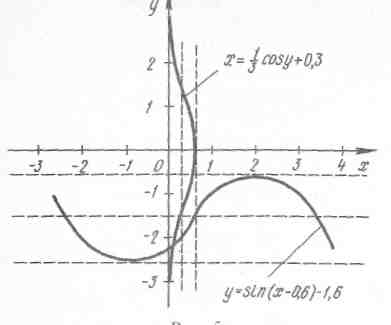 найти розв’язок системи:

Перепишемо систему у вигляді:

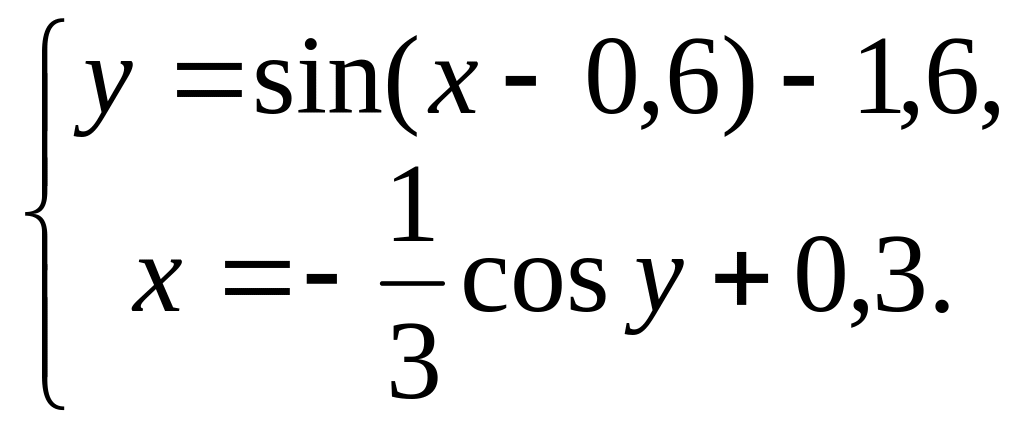
Відокремлення коренів можна провести графічно. Легко бачити, що система має один розв’язок, що належить області D: 0<x<0,3; -2,2<y<-1,8.

Потрібно переконатись, що система може бути розв’язана методом ітерацій. Для цього запишемо систему у вигляді: _{. Оскільки , то в о області D маємо}

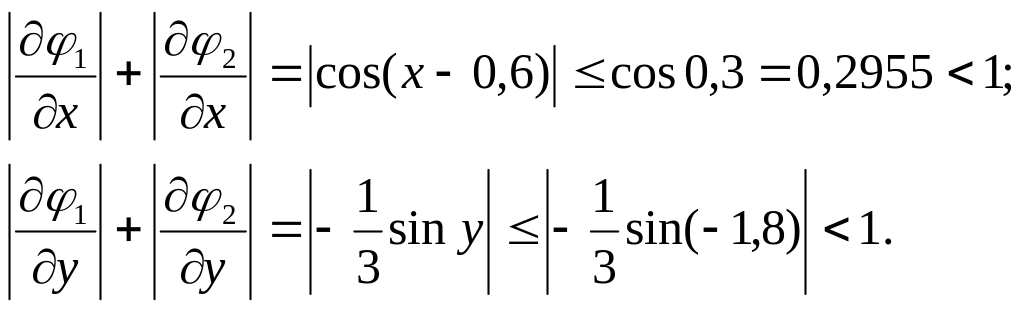
Отже, умови збіжності виконуються.

Обчислення виконуються за формулами:

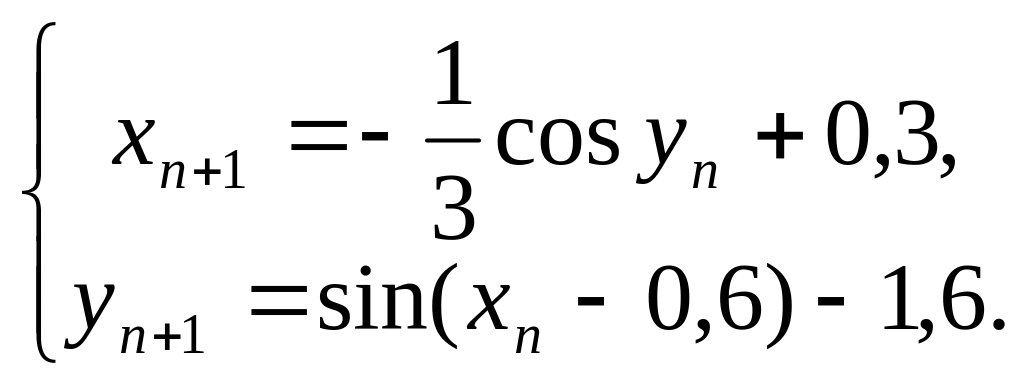
_{За початкове наближення візьмемо х0=0,15, у0=–2.}

Складемо таблицю:

п	xn	yп	xn–0,6
0	0,15	-2	-0,45	-0,4350	–0,4161	–0,1384
1	0,1616	-2,035	-0,4384	-0,4245	–0.4477	– 0,1492
2	0,1508	-2.0245	-0,4492	-0,4342	-0,4382	–0,1461
3	0,1539	-2,0342	– 0,4461	-0,4313	-0,4470	–0,1490
4	0,1510	-2,0313	-0,4490	-0,4341	-0,4444	–0,1481
5	0,1519		–0,4481	-0,4333	-0,4469	–0,1490
6	0,1510	-2,0333	0,449	-0,4341	-0,4462	-0,1487
7	0,1513	2,0341	-0,4487	-0,4340	-0,4469	-0,1490
8	0,1510	2,0340

_{Відповідь:} .

3 Використовуючи метод Ньютона розв’язати систему нелінійних рівнянь з точністю до 0,01.

Уточнення коренів виконують по формулам:

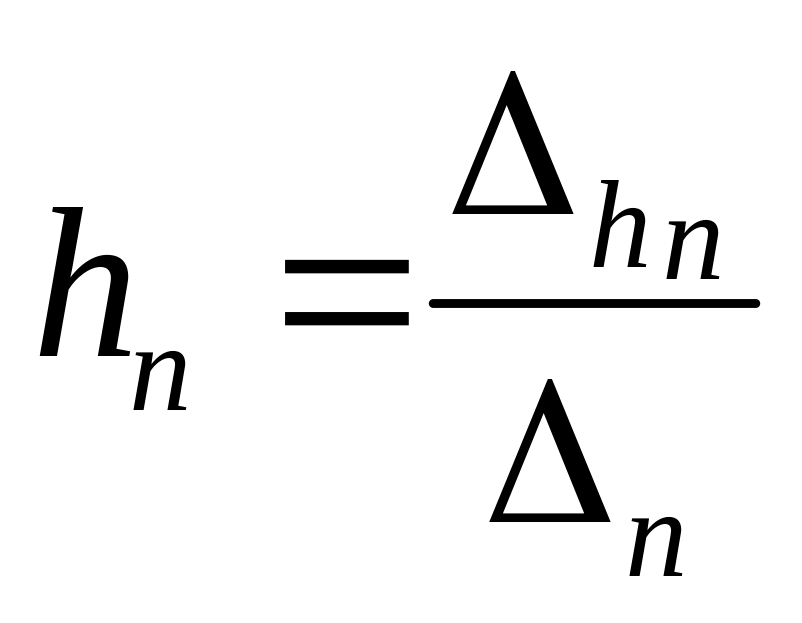_, , _{де ,}

Виконаємо відокремлення коренів графічно (для цього можна побудувати таблицю точок)

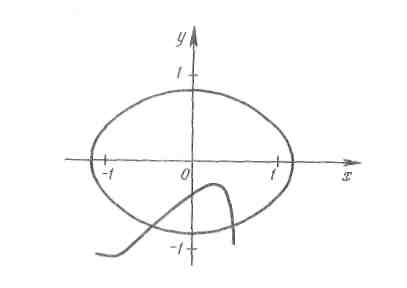Дана система має два розв’язки. Уточним один з них, що належить області D: 0,4<x<0,5; -0.76<y<-0,73. За початкове наближення візьмемо х₀=0,4; у₀=-0,75.

Маємо:

_,

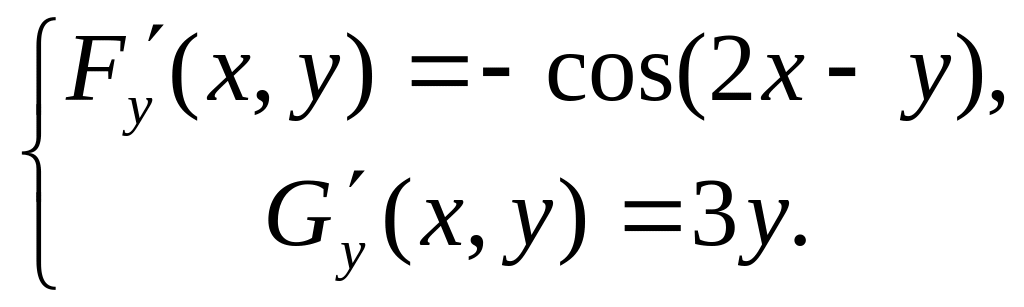
Всі обчислення можна оформити в таблиці:

n	xn			sin(2xn-yn)
	yn			cos(2xn-yn)
	0,4	0,128	0,55	0,9988	0,1198	-1,1584	-0,0208	2,6197	0,2701	0,10
	-0,75	0,8438		0,0208	-0,0282	0,64	- 2.25		0,0440	0,017
	0,50	0,2	0,733	0,9869	-0,0131	-1,523	0,1615	3,2199	-0,0193	-0,0060
	-0.733	0,8059		-0,1615	0,059	0,8	-2,199		0,0794	0,0247
	0,4940	0.1952	1 6963	0,9921	-0,0007	-1,4502	0,1251	2,9827	-0,0080	-0,0027
	-0,7083	0,7525		-0,1251	-0,0523	0,7904	-2,1249		-0,0764	-0,0256
	0,4913	0,1931	1,7165	0,9894	-0,0002	-1,4904	0,1452	3,1673	-0,0003	-0,0001
	-0,7339	0.8079		-0,1452	0.0010	0,7861	-2,2017		0,0013	0,0004
	0,4912	Відповідь:
	-0,7335

Теоретичні завдання:

1. Які рівняння відносяться до нелінійних?

2. Які рівняння відносяться до трансцендентних?

3. Що є розв‘язком нелінійного рівняння?

4.  Класифікація рівнянь,

5. Трансцендентні та алгебраїчні рівняння.

6. Які рівняння відносяться до трансцендентних рівнянь?

7. Які рівняння відносяться до алгебраїчних рівнянь?

8. Суть відокремлення коренів нелінійних рівнянь.

9. Суть методів уточнення коренів.

10. Які способи використовуються для відокремлення коренів?

11. В чому суть аналітичного методу відокремлення коренів?

12. Які теореми використовуються для аналітичного методу відокремлення коренів?

13. В чому суть алгоритму методу половинного ділення? Дайте геометричну інтерпретацію цього методу.

14. Графічна інтерпретація методу половинного ділення та основні формули методу.

15. В чому суть алгоритму методу хорд? Дайте геометричну інтерпретацію цього методу.

16. Графічна інтерпретація методу хорд та основні формули методу.

17. В чому суть алгоритму методу січних? Дайте геометричну інтерпретацію цього методу.

18. Графічна інтерпретація методу січних та основні формули методу.

19. В чому суть алгоритму комбінованого методу? Дайте геометричну інтерпретацію цього методу.

20. Графічна інтерпретація комбінованого методу та основні формули.

21. В чому суть алгоритму автоматизації пошуку рухомого кінця хорди?

22. В чому суть алгоритму автоматизації пошуку рухомого кінця січної?

23. Покажіть особливості методу ітерацій та його обмеження.

24. Графічна інтерпретація методу ітерацій та основні формули методу.

РОЗДІЛ 3. Розв’язування задач лінійної алгебри