Тема 2.2. Методи розв’язування систем нелінійних рівнянь
Метод Ньютона: суть методу, збіжність методу. (СРС)
Модифікований метод Ньютона. (СРС)
В результаті вивчення теми студенти повинні:
Знати – суть методу Ньютона, алгоритм методу, формули для дослідження збіжності методу.
Вміти – розв’язувати системи нелінійних рівнянь методом Ньютона та модифікованим методом Ньютона.
Завдання:
Опрацювати теоретичний матеріал, наведений в методичці, а також скористатись книгою Самарський А.А., Гулин А.В. Численные методы. (папка «Підручники») стор. 207-214, Калиткин Н.Н. Численные методы, стор. 152.
Коссак о., Тумашова о., Коссак о. – Методи наближених обчислень: Навчальний посібник, стор.30-32
Виконати завдання згідно номеру по списку в журналі з методички «Тестові завдання.doc»
Теоретичні завдання:
В чому особливість методу Ньютона?
Що є умовою збіжності методу?
Навести формули модифікованого методу Ньютона.
Метод Ньютона для системи . Якщо визначено початкове наближення x(0)=(x1(0), x2(0),..., xn(0))T, ітераційний процес знаходження розв’язку системи (2.10) методом Ньютона можна представити у вигляді
k=0,1,2.
(2.12)
де значення приростів Δx1(k), Δx2(k),., Δxn(k) визначаються з розв’язання системи лінійних рівнянь, всі коефіцієнти якої виражаються через відоме попереднє наближення x(k) = (x1(k) , x2(k) ,..., xn(k) )
(2.13)
У векторний-матричній формі розрахункові формули мають вигляд
x(k+1) = x(k) + ∆x(k), k=0,1,2… k = 0,1, 2,...
Де вектор
знаходиться
з розв’язку рівняння f(x(k))+J(x(k))∆x(k)=
0,
(2.15)
де
-
матриця Якобі перших похідних
вектор-функції f(x).
Виражаючи з (2.15) вектор приростів Δx(k) і підставляючи його в (2.14), ітераційний процес знаходження розв’язку можна записати у вигляді
x(k+1)=x(k)–J-1 (x(k))f(x(k)) k = 0,1,2... (2.16)
де J-1(x) - матриця, зворотна матриці Якобі. Формула (2.16) є узагальнення формули (2.2) на випадок систем нелінійних рівнянь.
При реалізації алгоритму методу Ньютона в більшості випадків переважним є не обчислення зворотної матриці J-1(x(k)) а знаходження з системи (2.13) значень приростів Δх1(k), Δх(2k),…,Δх(пk) і обчислення нового наближення по (2.12). Для вирозв’язку таких лінійних систем можна привертати самі різні методи, як прямі, так і ітераційні, з урахуванням розмірності п вирішуваної задачі і специфіки матриць Якобі J(x) (наприклад, симетрії, розрідженості і т.п.).
Використання методу Ньютона припускає дифференційованість функцій f1(x), f2(x),…, fn(x) і невиродженість матриці Якобі (detJ(x(k))≠0).
У випадку, якщо початкове наближення вибране в достатньо малій околиці шуканого кореня, ітерації сходяться до точного розв’язку, причому збіжність квадратична.
У практичних обчисленнях як
умова закінчення ітерацій зазвичай
використовується критерій
,
де ε- задана точність. (2.17)
Приклад Методом Ньютона знайти позитивний розв’язок системи нелінійних рівнянь
(2.18)
з точністю ε
= 104.
Р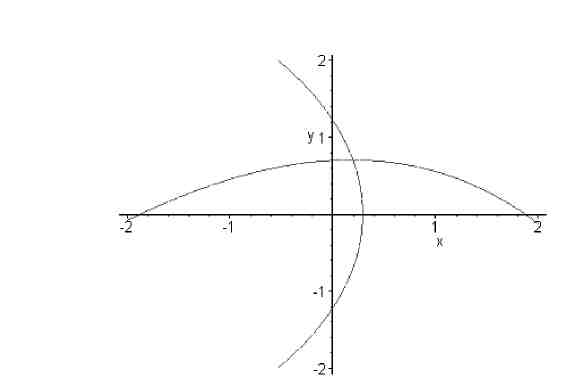
ішення:
Для вибору початкового наближення
застосовуємо графічний спосіб. Побудувавши
на площині (x1,x2)
в області, що цікавить нас,
криві f1(x1,x2)
= 0 і f2(x1,x2)
= 0 (мал. 2.2), визначаємо,
що додатній розв’язок системи рівнянь
знаходиться в квадраті 0<x1<0,5,
0,5 <x2
< 1,0.
За початкове наближення приймемо x1(0)=0,25, x2(0)=0,75. Для системи двох рівнянь розрахункові формули (2.12), (2.13) зручно записати у вигляді відносно x(k+1), x(k+1)
(2.19)
де
У даному прикладі:
f1 ( x 1( k) ,x2(k)) = 0,1x1( k)2+x1(k)+0,2x2(k)2-0,3
f2(x 1(k) ,x2(k)) = 0,2x 1( k)2 +x2(k)-0,1x1(k)x2(k)-0,7
Підставляючи в праві частини співвідношень (2.19) вибрані значення x 1(0), x(20), одержимо наближення x1(1), x(21), використовуване, у свою чергу, для знаходження x 1(2), x22). Ітерації тривають до виконання умови (2.17), де
Результати обчислень містяться в таблиці 2.4.
до |
|
|
|
|
|
|
|
0 |
0.25000 0.75000 |
0.06875 0.04375 |
1.01250 0.02500 |
0.30000 0.97500 |
0.05391 |
0.04258 |
0.97969 |
1 |
0.19498 0,70654 |
-0.00138 0,00037 |
1.00760 0,00734 |
0.28262 0,98050 |
- 0,00146 |
0.00038 |
0.98588 |
2 |
0.19646 0.70615 |
0.00005 0.00000 |
1.00772 0.00797 |
0.28246 0.98035 |
0.00005 |
0.00000 |
0.98567 |
3 |
0.19641 0.70615 |
|
|
|
|
|
|
x 1(*) ≈0.1964, x2(*) ≈0.7062.