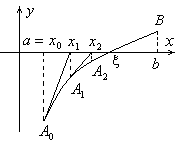- •Похибки заокруглювання Похибка функції
- •Похибка функції
- •Тема 1.1. Розв’язування нелінійних рівнянь
- •Метод простої ітерації
- •Дане рівняння зведемо до вигляду
- •Метод січних (хорд).
- •Тема 2.2. Методи розв’язування систем нелінійних рівнянь
- •Коссак о., Тумашова о., Коссак о. – Методи наближених обчислень: Навчальний посібник, стор.30-32
- •Використовуючи метод ітерацій розв’язати систему нелінійних рівнянь з точністю до 0,01.
- •Тема 3.1. Методи розв’язування систем лінійних рівнянь
- •Опрацювати теоретичний матеріал, наведений в методичці, а також скористатись книгою Самарський а.А., Гулин а.В. Численные методы. (папка «Підручники») стор. 82-95
- •Коссак о., Тумашова о., Коссак о. – Методи наближених обчислень: Навчальний посібник, стор. 40-45
- •Метод Зейделя.
- •Розв’язування систем n-лінійних рівнянь з n-невідомими за формулами Крамера.
- •Тема 3.2: Методи обчислення визначників та знаходження власних значень матриць
- •Тема 4.1: Інтерполяція фунцій
- •Опрацювати теоретичний матеріал, наведений в методичці, а також скористатись книгою Самарський а.А., Гулин а.В. Численные методы. (папка «Підручники») стор. 127-140
- •Коссак о., Тумашова о., Коссак о. – Методи наближених обчислень: Навчальний посібник, стор. 52-59
- •Інтерполяційний многочлен Ньютона для нерівновіддалених вузлів
- •Інтерполяційний многочлен Ньютона для рівновіддалених вузлів
- •Обернене інтерполювання
- •Числове диференціювання
- •Ітераційно-інтерполяційний метод Ейткена
- •Тема 4.2: Апроксимація функцій
- •Опрацювати теоретичний матеріал, наведений в методичці, а також скористатись книгою Самарський а.А., Гулин а.В. Численные методы. (папка «Підручники») стор. 140-148
- •Сплайн-апроксимація
- •Тема 4.3. Сплайн-інтерполяція
- •. Кубічна сплайн-інтерполяція.
- •5. Багатомірний інтерполяційний сплайн.
- •Розділ 5. Числове інтегрування
- •Тема 5: Числове інтегрування
- •Коссак о., Тумашова о., Коссак о. – Методи наближених обчислень: Навчальний посібник, стор. 75-80
- •Метод Гауса
- •Які переваги та недоліки методу Гауса?
- •Знайти значення інтеграла методом Гауса:
- •Тема 6: Основні методи мінімізації функцій.
- •Коссак о., Тумашова о., Коссак о. – Методи наближених обчислень: Навчальний посібник, стор. 100
- •Тема 7.1. Наближене розв’язування задачі Коші для звичайних диференціальних рівнянь
- •Модифікації методу Ейлера
- •Метод Рунге–Кутта
- •Методи прогнозу і корекції (багатоточкові методи)
- •Метод Мілна
- •Метод Адамса - Башфорта
- •Контрольні питання:
- •Тема 7.2. Наближене розв’язування крайових задач для звичайних диференціальних рівнянь
- •Метод прогонки
- •Розділ 7. Наближене обчислення диференціальних рівнянь. Тема 7.3. Наближене розв’язування диференціальних рівнянь з частинними похідними
- •Еліптичні рівняння
Дане рівняння зведемо до вигляду
 процес
ітерацій збіжний.
процес
ітерацій збіжний.
Візьмемо за перше наближення х0 = 0,25 – середину відрізка [0; 0,5]. Обчислення будемо вести за формулою
![]()
-
n
xn
xn+1
0
0,25
0
x* =0,20164
,203131
0,20313
0,20168
2
0,20168
0,20164
3
0,20164
0,20164
При знаходженні двох інших коренів
методом ітерацій вже не можна скористатись
формулою
![]() ,
оскільки
,
оскільки
![]()
В цьому випадку рівняння потрібно
представити у вигляді, наприклад,
![]() Тоді на відрізках [–3; –2], [2, 3] умова
Тоді на відрізках [–3; –2], [2, 3] умова
![]() буде виконуватись.
буде виконуватись.
Таким чином при практичному знаходженні
кореня за методом ітерації при переході
від рівняння f(x)
= 0 до (1) необхідно зобразити
![]() так, щоб похідна
так, щоб похідна
![]() за
абсолютною величиною була якомога менша
одиниці.
за
абсолютною величиною була якомога менша
одиниці.
Для зведення рівняння f(x) = 0 до вигляду (1) може бути застосований загальний метод, котрий забезпечує виконання нерівності (3).
Нехай
![]() (4)
(4)
при
, де m1 – найменше
значення похідної
![]() ,
,
![]() ;
;
М1 – найбільше значення
похідної на відрізку [a,
b],
![]()
Якщо похідна – від’ємна, то замість рівняння f(x)=0 розглянемо рівняння–f(x)=0.
Замінимо це рівняння f(x)
= 0 еквівалентним йому рівнянням
![]() і виберемо сталу λ
так, щоб забезпечити виконання умови
(3)
і виберемо сталу λ
так, щоб забезпечити виконання умови
(3)
![]() .
.
1)
![]() Розкриваємо
нерівність
Розкриваємо
нерівність
![]()
Візьмемо праву нерівність
![]() ,
з неї випливає, що
,
з неї випливає, що
![]() тобто
тобто
![]() оскільки
оскільки
![]() З лівої нерівності
З лівої нерівності
![]() випливає, що
випливає, що
![]()
Отже, значення коефіцієнта
λ знаходиться в межах
![]()
![]() <
<![]() <0
як правило за λ приймають значення
<0
як правило за λ приймають значення
![]() де М1 – максимальне значення
похідної
на
проміжку [a, b].
де М1 – максимальне значення
похідної
на
проміжку [a, b].
Відповідно, ітераційна формула буде
мати вигляд
![]()
2) Якщо
![]() то можна довести, що
то можна довести, що
![]() . (5)
. (5)
І відповідний ітераційний процес має
вигляд
![]() (6)
(6)
Приклад. Рівняння
![]() звести до вигляду, що допускає використання
методу ітерацій. Корінь відокремлений
на відрізку [1; 2].
звести до вигляду, що допускає використання
методу ітерацій. Корінь відокремлений
на відрізку [1; 2].
![]() .
.
Тоді
![]() ,
виберемо λ так, щоб
,
виберемо λ так, щоб
![]() для
для
![]()
![]() .
.
Звідси ![]()

Оскільки ![]() .
То на [1; 2]
.
То на [1; 2]
![]() Значення
λ можна визначити і таким способом.
Значення
λ можна визначити і таким способом.
Оскільки f’(x)
> 0, [1; 2], то ![]()
Знайдемо, що
![]() .Звідси
.Звідси
![]() (7)
(7)
Метод Ньютона (дотичних)
Нехай корінь рівняння
![]() відділений на відрізку
відділений на відрізку
![]() ,
причому функції
,
причому функції
![]() ,
,
![]() неперервні і зберігають знаки на всьому
відрізку
.
неперервні і зберігають знаки на всьому
відрізку
.
Геометричний зміст методу
Ньютона полягає в тому, що дуга кривої
![]() замінюється дотичною до цієї кривої
(звідси й друга назва – метод дотичних).
замінюється дотичною до цієї кривої
(звідси й друга назва – метод дотичних).
Перший випадок.
Нехай
![]() ,
,
![]() ,
,
![]() ,
,
![]() (рис.1) або
(рис.1) або
![]() ,
,
![]() ,
,
![]() ,
,
![]() (рис.2).
(рис.2).
Рис.1 |
Рис.2 |
Проведемо дотичну до кривої
в точці
![]() і знайдемо абсцису точки перетину
дотичної з віссю
і знайдемо абсцису точки перетину
дотичної з віссю
![]() .
рівняння дотичної в точці
має вигляд
.
рівняння дотичної в точці
має вигляд
![]() .
.
Покладаючи
![]() ,
,
![]() ,
отримаємо
,
отримаємо
![]() .
Тепер
.
Тепер
![]() .
Знову застосуємо метод Ньютона
.
Знову застосуємо метод Ньютона
 і в загальному випадку маємо
і в загальному випадку маємо
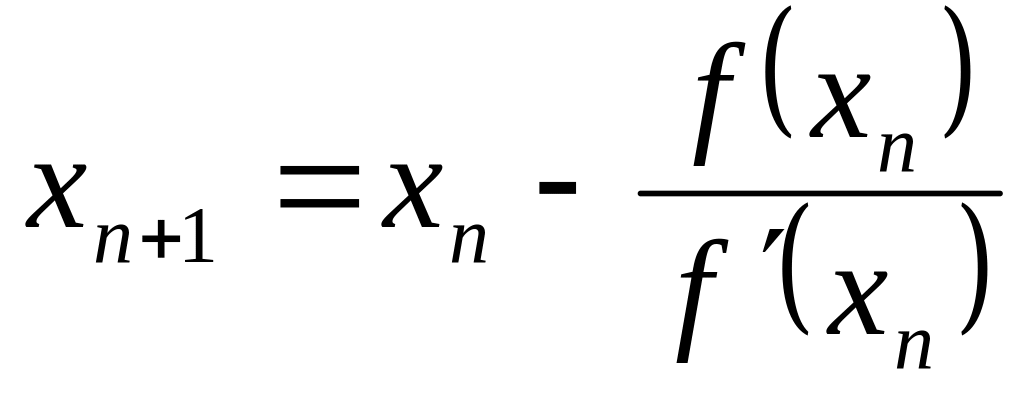 .
.
Отримуємо послідовність
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Рис.3 |
Рис.4 |
Другий випадок.
Нехай
,
,
,
(рис.3) або
,
,
![]() ,
(рис.4).
,
(рис.4).
Якщо провести дотичну до
кривої
![]() в точці
в точці
![]() ,
то вона перетне вісь абсцис у точці, що
не належить
,
то вона перетне вісь абсцис у точці, що
не належить
![]() .
Тому проведемо дотичну у точці
.
Тому проведемо дотичну у точці
![]() і запишемо її рівняння
і запишемо її рівняння
![]() .
Покладаючи
,
,
знаходимо
.
Покладаючи
,
,
знаходимо
![]() .
Корінь
.
Корінь
![]() .
Застосуємо метод Ньютона
.
.
Застосуємо метод Ньютона
.
Правило. Як початкову точку треба вибирати той кінець відрізку , в якому знак функції співпадає зі знаком другої похідної.
Якщо
![]() ,
то
,
то
![]() ,
а якщо
,
а якщо![]() ,
то
,
то
![]() .
.