Метод Адамса - Башфорта

Цей метод також має четвертий порядок точності. Формула, що використовується в ньому отримана інтегруванням оберненої інтерполяційної формули Ньютона і має вид

          (9.41)

На етапі корекції використовується формула

          (9.42)

Розрахунки по методу Адамса - Башфорта виконуються так як і по методу Мілна, але на відміну від останнього похибка, внесена на якому-небудь кроці, не має тенденції до експоненціального росту.

Можна припустити, що так як величина відкиненого члену відома, то її можна використовувати для уточнення скоректованого значення залежної змінної. Так як внесення поправок в корегуючий член може негативно вплинути на стійкість рахунку, то для підвищення точності рахунку слід використовувати методи більш високих порядків точності.

Приклад 1.2. Розглянемо приклад розв’язання відомої інженерної задачі на ЕОМ за допомогою методу Рунге-Кутта.

З задачами про удар і коливання часто стикаються в аерокосмічній промисловості і на транспорті, де існують багато численні джерела коливань. Видалення ударних й вібраційних навантажень має виключно велике значення для забезпечення нормальної роботи приборів й систем управління й створення комфортних умов для екіпажу. Звичайно для захисту від великих вібрацій в конструкцію транспортного засобу вводять пружні опори, що забезпечені пристроями, що забезпечують деяке демпфіроване коливання. Такі опори різко зменшують частоти власних коливань конструкції, забезпечуючи їх суттєву відмінність від частот збуджуючих силових факторів. Такий розв’язок ефективний як засіб захисту від стаціонарних коливань, однак в випадку ударних навантажень піддатливість опор може призвести до недопустимо великих зміщень.

     

     Рисунок 9.13 – Графічне представлення використання пружних опор в транспортних засобах

Відомо, що від цього недоліку вільні системи підвіски, в яких використовуються пружини з симетричною нелінійною характеристикою жорсткість яких прогресивно збільшується при більших відхиленнях от робочої точки.

Пристрій, показаний на рисунку 9.13, складається з маси т, зв'язаною з жорсткою стінкою через пружину постійної жорсткості k, демпфер з коефіцієнтом демпфірування с й пружиною з нелінійною характеристикою утворюючої відновлюючу силу, рівну добутку постійної k на зміщення в третій степені. Така пружина має симетричну нелінійну характеристику, забезпечуючи захист від ударних й вібраційних навантажень. Так як рух цієї системи описується нелінійним диференціальним рівнянням:

,

то традиційні «точні» методи не дозволяють знайти залежність зміщення х від часу. Тому для розв'язку вказаного рівняння прийдеться скористатись чисельним методом. Нехай параметри системи мають наступні значення:

k=2,0 Н/см; k* = 2, 0 Н/см³; с = 0,15 Нс/см; m=1,0 кг,

а початкові умови задані в вигляді: х(0) - 10 см, х(0)=0.

Підготуємо й реалізуємо на ЕОМ програму для моделювання руху даної механічної системи в інтервалі часу 0 t 1 .

Щ об розв'язати цю задачу однокроковим чисельним методом, необхідно звести диференціальне рівняння другого порядку до двох диференціальних рівнянь першого порядку за допомогою допоміжної змінної , . В результаті отримаємо:

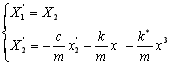
Щоб при видачі довжина виражалась в сантиметрах, змінимо розмірністьмаси. Тоді m=0,01 Н?с² /см.

    

З приведеного графіка залежності зміщення від часу видно, що частота коливань залежить від амплітуди. Саме так звичайно і ведуть себе нелінійні системи, що мають пружини, жорсткість яких при стискові збільшується.