Тема 4.3. Сплайн-інтерполяція

Кубічна сплайн-інтерполяція.

Багатомірний інтерполяційний сплайн.

В результаті вивчення теми студенти повинні:

Знати – властивості кубічної сплайн-інтерполяції, правила побудови багатомірного інтерполяційного сплайна, поняття системи фундаментальних сплайнів,

Вміти – будувати кубічний сплайн, будувати систему фундаментальних сплайнів,

Завдання:

1. Опрацювати теоретичний матеріал, наведений в методичці, також знайти відповідний теоретичний матеріал в підручнику Самарський А.А., Гулин А.В. Численные методы. (папка «Підручники»), стор. 142-148

2. Боглаев Ю.П. Вычислительная математика и программирование: Учебное пособие для студентов втузов, стор.256-259

3. Дати відповіді на питання:

1. Навести формули кубічної сплайн- інтерполяції.

2. У якому випадку можна побудувати двомірну сплайн-інтерполяцію?

3. Які додаткові граничні умови потрібні для побудови багатомірного сплайна?

. Кубічна сплайн-інтерполяція.

Якщо носієм сплайн-функціїї кубічна парабола, то можна побудувати два кубічні сплайни:

(2.32)

(2.33)

У першому випадку (2.32) умові гладкого сполучення кубічних парабол піддаються перші і другі похідні, в другому випадку (2.33) кубічні параболи у вузлах сплайна сполучаються тільки по першій похідній.

5. Багатомірний інтерполяційний сплайн.

Якщо замість поліномів в запропонованій вище схемі використовувати сплайн-функції, то аналогічно можна побудувати двовимірний інтерполяційний сплайн. Проте існують і інші схеми побудови багатовимірних інтерполяційних сплайнів. Розглянемо одну з них.

Системою фундаментальних сплайнів на інтерполяційній сітці називаються сплайн-функції, що задовольняють умовам:

(2.37)

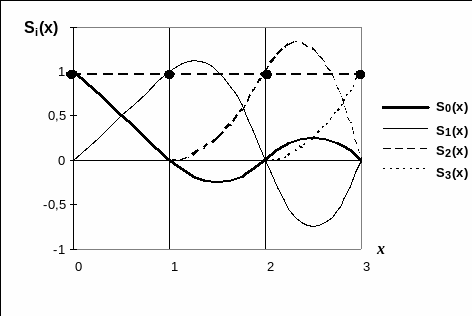
У таблиці 2.2. приведені умови інтерполяції для фундаментальних сплайнів . Як видно з таблиці, кожен інтерполяційний сплайн у вузлах інтерполяції n разів перетинає координатну вісь (нулі сплайна) і лише в одному вузлі, співпадаючому по номеру з номером сплайна, рівний 1. На рис.2.6 показана система інтерполяційних сплайнів для сітки

Рис. 2.6. Система фундаментальных интерполяционных сплайнов

Рис. 2.6. Система фундаментальных интерполяционных сплайнов

Аналогічним чином можна побудувати систему фундаментальних сплайнів для незалежної змінної у :

(2.38)

тоді двовимірний інтерполяційний сплайн можна представити таким чином:

(2.39)

де - значення функції у вузлових точках інтерполяційної сітки. .

Враховуючи властивості одновимірних фундаментальних сплайнів (2.37 - 2.38), неважко переконатися, що двовимірний сплайн (2.39) вирішує початкову задачу інтерполяції функції тобто . У формулі (2.39) автоматично закладені умови гладкого сполучення шматків поверхонь, з яких складається сплайн-функція, по лініях «склеювання» цих поверхонь (у нашому випадку по межах часткових прямокутників інтерполяційної сітки).

При побудові фундаментальних сплайнів (2.37-2.38) потрібні додаткові граничні умови. Останні можна отримати, використовуючи додаткові відомості про поведінку функції на межі інтерполяційної сітки, або в результаті оптимізації деякого критерію оцінки якості рішення інтерполяційної задачі.

Неважко показати, що при побудові сплайна із звільненими граничними умовами, коли його другі приватні похідні рівні 0 на межі інтерполяційної сітки, в загальному випадку потрібний, щоб другі похідні фундаментальних сплайнів на кінцях відрізків інтерполяції також були рівні 0.