Розділ 1. Елементи теорії похибок

Тема 1: Елементи теорії похибок

Похибки заокруглювання.

Дії над наближеними числами.

Похибка функції.

В результаті вивчення теми студенти повинні:

Знати – механізми округлення чисел в обчислювальній машині;

правила округлення суми, добутку, різниці і частки чисел.

Вміти – обчислювати похибку, що виникає під час заокруглювання шляхом відкидання розрядів; виконувати округлення суми, добутку, різниці і частки чисел; обчислювати точність результатів.

Завдання:

1. Опрацювати теоретичний матеріал, наведений в методичці, а також скористатись книгою Самарський А.А., Гулин А.В. Численные методы. (папка «Підручники») стор. 16-25

2. Коссак О., Тумашова О., Коссак О. – Методи наближених обчислень: Навчальний посібник, стор.7-13

3. Виконати обчислення:

Скласти кілька наближених чисел:

Знайти добуток наближених чисел і всі цифри яких вірні.

4. Дати відповіді на контрольні питання:

1. Які причини появи похибок?

2. Назвіть типи похибок та джерела їх виникнення.

3. Що називається абсолютною похибкою? Які форми її запису вам відомі?

4. Що називається відносною похибкою?

5. З чим пов’язане виникнення похибок заокруглювання?

Похибки заокруглювання Похибка функції

У комп’ютерах і калькуляторах числа наводять з обмеженою кількістю розрядів, що визначена розрядною сіткою пристрою. Типова форма зображення дійсних чисел у комп’ютері така:

a =m 10^p , 0,1 < 1

Під час виконання арифметичних операцій відбувається відкидання зайвих розділів. Результат можна записати у такому загальному вигляді:

y = m_y 10^Py + g _y 10^{Py – t},

де t – кількість значущих цифр (довжина розрядної сітки ), 0 g < 1.

Приклад. Розглянемо механізм додавання двох чисел 162,4 і 1,769 в уявній чотири-розрядній обчислюваній машині, яка працює у десятковій системі числення.

0,1624 10³

0,1769 10¹

вирівнювання 0,1624 10³

порядків 0,001769 10³

0,164169 10³ = 0,1641 10³ + 0,69 10^-1

Зайві розряди (6 і 9) будуть відкинуті, що спричинює появу обчислювано похибки.

Розглянемо похибку, що виникає під час заокруглювання шляхом відкидання зайвих розрядів. Вона буде максимальною, коли (g _y) _max = 1 і (m_y)_min = 0,1. Відносна похибка у цьому випадку

(1.1)

З (1.1) випливає, що відносна похибка заокруглювання шляхом відкидання зайвих розрядів є сталою і залежить від довжини розрядної сітки комп’ютера.

Найчастіше використовують симетричне заокруглювання. Якщо старший з розрядів, що буде відкинутий менше 5, то остання з цифр, які залишилися, не змінюється незмінною, у протилежному випадку (≥ 5) наймолодший розряд з тих, що залишилися, збільшується на одиницю:

У цьому випадку абсолютна похибка

звідки випливає, що (у)_max ≤ ½ 10^p-t .Тоді найбільша відносна похибка симетричного заокруглювання

Отже, похибка симетричного заокруглювання вдвічі менша, ніж похибка заокруглювання шляхом відкидання зайвих розрядів.

Зазначимо, що в комп’ютерах дані наводять у двійковій системі числення, і під час виконання дій використовується двійкова арифметика.

Приклад. Заокруглити число 4,256724 до шести, п’яти, чотирьох і трьох значущих цифр.

Розв’язування. Отримаємо наближені числа 4,25672, 4,2567, 4,257, 4,26 з найбільшими похибками симетричного заокруглювання

Похибка функції

Розглянемо функцію , параметри якої являють собою наближені числа з абсолютною похибкою .

Абсолютна похибка функції визначається як сума абсолютних похибок параметрів функції помножених на вагові коефіцієнти , які характеризують швидкість зміни функції при зміні кожного параметра.

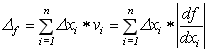                    (1)

Відносна похибка може бути визначена сумою абсолютних похибок параметрів функції помножених на вагові коефіцієнти, які представляють собою модуль часткової похідної логарифма функції по відповідному параметру.

                    (2)

Якщо функція являє собою суму параметрів, то абсолютна похибка теж є сумою похибок:

Якщо                , то      (3)

Якщо функція представляє собою добуток параметрів, то і відносна похибка також представляє добуток:

Якщо                , то      (4)

Теорема 1. Абсолютна похибка алгебраїчної суми декількох наближених чисел не перевищує суми абсолютних похибок цих чисел.

Наслідок. Гранична абсолютна похибка алгебраїчної суми декількох наближених чисел рівна сумі гранично абсолютних похибок цих чисел.

При складанні наближених чисел з різною абсолютною похибкою рекомендується діяти наступним чином:

• виділити число ( або числа) найменшої абсолютної точності;

• найбільш точні числа округлюють таким чином, щоб зберегти в них на один знак більше, ніж у виділеному числі;

•  виконати додавання, враховуючи всі збережені знаки;

• отриманий результат заокруглити на один знак.

Приклад 1. Скласти кілька наближених чисел:

У кожному з приведених чисел вірні всі значущі цифри (у широкому змісті).

Розв‘язок. Виділяємо два числа найменшої точності 204,4 і 144,2. Обидва вони визначені з точністю до 0,1. Отже, інші числа округлюються з точністю до 0,01. Округлимо і складемо ці числа. В результаті отримуємо число 374,19.

Округляючи це число до 0,1 остаточно одержимо а = 374,2. Оцінимо точність результату. Для цього знайдемо повну похибку, яка складається з трьох значень:

1) суми граничних похибок вихідних даних

2) абсолютної величини суми похибок (з обліком зі знаків) округлення

3) кінцевої похибки округлення результату

Отже,

Таким чином, переконуємося, що остаточна похибка не менше граничної абсолютної похибки найменш точного з чисел які додаються (дійсно, 0,3 > 0,01).

Приклад 2. Обчислити значення функції y=1-cosx для наступних значень аргументу: 1) х = 80°; 2) x= 1°. Підрахувати граничні абсолютну та відносну похибку результату.

Розв‘язок. 1) знаходимо: соs 80° = 0,1736 і оскільки всі цифри цього числа вірні у вузькому змісті, то . Тоді та (з точного числа, рівного одиниці, віднімається наближене число абсолютна похибка якого, не перевищує 0,00005). Отже,

Маємо

тобто,

з наведених прикладів видно, що для малих значень аргументу безпосередній розрахунок по формулі y=1-cosx дає відносну похибку порядку 25%. Для така похибка складає всього лише 0,006%.

Змінимо чисельну схему і для обчислення значень функції y=1-cosx при малих значеннях аргументу скористаємося формулою

Позначимо тоді

Але         

У результаті отримаємо (а раніше мали ). Таким чином, просте перетворення розрахункової формули дозволило одержати більшу точність.

Теорема 2. Відносна похибка добутку декількох наближених чисел, відмінних від нуля не перевищує суми відносних похибок цих чисел.

Доведення. Нехай                          (5)

Для визначеності припустимо, що наближені числа позитивні і мають абсолютні похибки відповідно.

Для оцінки похибки добутку прологарифмуємо вираз (5):

               (6)

Абсолютна похибка алгебраїчної суми декількох наближених чисел (6) не перевищує суми абсолютних похибок цих чисел, тобто

          (7)

Використовуючи наближену формулу

                         (8)

Одержимо                         (9)

Звідки                         (10)

Зазначимо, що знак модуля у виразі (9) виключений, тому що було прийнято, що , (і = 1, 2, ... , n).

Наслідок. Гранична відносна похибка добутку дорівнює сумі граничних відносних похибок співмножників

Приклад 3. Знайти добуток наближених чисел і всі цифри яких вірні.

Розв‘язок. У першому числі дві вірні значущі цифри, а в другому – п'ять. Тому друге число округляємо до трьох значущих цифр. Після округлення маємо:

звідси               

У результаті залишені дві значущі цифри, тобто стільки, скільки їх мав співмножник з найменшою кількістю вірних значущих цифр.

Приклад 4. Визначити добуток наближених чисел і і число вірних знаків у ньому, якщо всі написані цифри співмножників вірні (у вузькому змісті).

Розв‘язок. В першому числі три вірні значущі цифри, в другому - чотири; можна перемножити числа без попереднього округлення: Варто залишити три значущі цифри, тому що найменш точний зі співмножників має стільки ж вірних значущих цифр; таким чином и=713. Підрахуємо похибку:

тоді Значить добуток u має два знаки і його варто записати так:

     Приклад 3. Визначити граничну відносну похибку і кількість вірних цифр добутку , де всі цифри співмножників вірні у вузькому змісті.

Розв‘язок. Обидва співмножники мають по чотири вірні цифри у вузькому змісті, тобто і . Тоді по формулі маємо

звідси слідує що добуток має три вірні цифри в вузькому змісті.

Перевіримо, чи насправді це так. Знайдемо добуток даних наближених чисел; він дорівнює . Визначимо граничну абсолютну похибку за формулою

Отримаємо Тоді

Отже, добуток має три вірні цифри в вузькому змісті.

Контрольні питання:

6. Які причини появи похибок?

7. Назвіть типи похибок та джерела їх виникнення.

8. Що називається абсолютною похибкою? Які форми її запису вам відомі?

9. Що називається відносною похибкою?

10. З чим пов’язане виникнення похибок заокруглювання?

РОЗДІЛ 2. Методи розв’язування нелінійних рівнянь та їхніх систем