1.1.7.1 Критерій 2 Пірсона.
З метою перевірки розглядатимемо емпіричні ni та теоретичні частоти ni' - попадання величини X в часткові інтервали (хі , х1+i) однакової довжини, на які ділять весь інтервал спостережуваних значень величини [6,7]. При рівні значимості а необхідно перевірити нульову гіпотезу: генеральна сукупність розподілена за законом А.
В якості критерію перевірки нульової гіпотези приймають випадкову величину
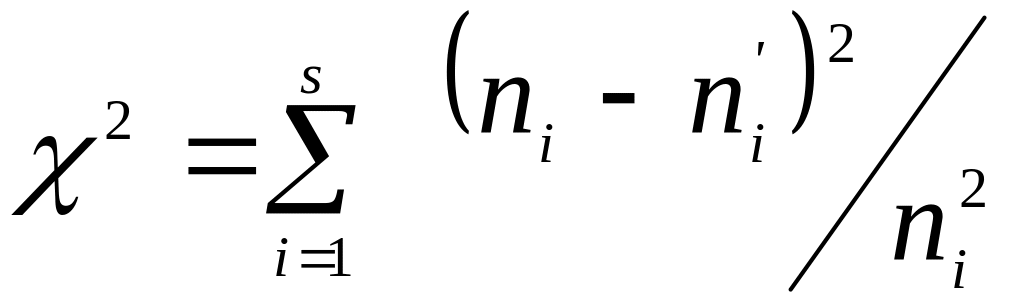(21)
де s - кількість часткових інтервалів.
Чим менше відрізняються емпіричні та теоретичні частоти, тим менша величина критерію, тобто він характеризує відмінність емпіричного та теоретичного розподілів.
Доведено, що при n∞ закон розподілу величини незалежно від того, за яким законом розподілена генеральна сукупність, наближається до закону розподілу 2 з k=s-r-i степінями свободи, де r - кількість параметрів закону розподілу, які наведені в результатах вимірювань. Критичні точки розподілу 2 приведені в таблиці 2. Правостороння критична область для критерію Пірсона 2>2 кр.(, k) це - область прийняття нульової гіпотези 2 <2 кр.(, k).
Таким чином, якщо необхідно перевірити, чи розподілена генеральна сукупність нормально, можна скористатися критерієм Пірсона. Один із способів вирішення цього завдання полягає в наступному.
1.Весь інтервал значень величини X, одержаних при спостереженнях., розбивають на s часткових інтервалів (xі, хі+1). В якості частоти пі і-го інтервалу вибирають число значень, які потрапили в і-ий інтервал. При цьому кількість спостережень п повинна бути достатньо великою, не менше 50. Кожен частковий інтервал повинен містити не менше 5 значень; інтервали з меншою кількістю значень об'єднують.
2.Розраховують середнє значення х та статистичну оцінку середнього квадратичного відхилення Sx ряду результатів спостережень.
3.
Нормують величину X,
тобто
переходять до величини
і
розраховують границі нових інтервалів
(zi;
zi+1)
, (22)
причому за z1 приймають - , а за zs+1 (права границя останнього часткового інтервалу) + .
4. Розраховують теоретичні ймовірності рi попадання X в інтервал (xi ,xi+]) з рівняння
, (23)
де Ф(z)- нормована функція Лапласа, і знаходять теоретичні частоти
n1i =прi .
Таблиця 2 - Критичні точки розподілу 2 .
Кількість степіней волі k
|
Рівень значимості
|
|||||
0,01 |
0,025 |
0,05 |
0,95 |
0,975 |
0,99 |
|
1
|
6,6
|
5,0
|
3,5
|
0,0039
|
0,00098
|
0,00016 )
|
2
|
9,2
|
7,4
|
6,0 |
0,103
|
0,051
|
0,020
|
3
|
11,3
|
9,4
|
7,8 |
0,352 |
0,216
|
0,115
|
4
|
13,3
|
11,1
|
9,5 |
0,711
|
0,484
|
0,297
|
5
|
15,1
|
12,8
|
11,1 |
1,15
|
0,831
|
0,554
|
6
|
l6,8
|
14,4
|
12,6 |
1,64
|
1,24
|
0,572
|
7
|
18,5
|
16,0
|
14,1 |
2,17
|
1,69
|
1,24
|
8
|
20,1
|
17,5
|
15,5 |
2,73
|
2,18
|
1,65
|
9
|
21,7
|
19,0
|
16,9 |
3,33
|
2,70
|
2,09
|
10
|
23,2
|
20,5
|
18,3 |
3,94
|
3,25
|
2,56
|
11
|
24,7
|
21,9
|
19,7 |
4,57
|
3,82
|
3,05
|
12
|
26,2
|
23,3
|
21,0 |
5,23
|
4,40
|
3,57
|
13
|
27,7
|
24,7
|
22,4 |
5,89
|
5,01
|
4,11
|
14 |
29,1 |
26,1
|
23,7 |
6,57
|
5,63
|
4,66
|
15
|
30,6 |
27,5
|
25,0 |
7,26
|
6,26
|
5,23
|
16
|
32,0
|
28,8
|
26,3 |
7,96
|
6,91
|
5,81
|
17
|
33,4
|
30,2
|
27,6 |
5,67
|
7,56
|
6,41
|
18
|
34,8
|
31,5
|
28,9 |
9,39
|
8,23 :
|
7,01
|
19
|
36,2
|
32,9
|
30,1
|
10,1
|
8,91
|
7,63
|
20
|
37,6
|
34,2
|
31,4
|
10,9 |
9,59 |
8,26 |
21 |
38,9
|
35,5
|
32,7
|
11,6
|
10,3
|
8,90
|
22
|
40,3
|
36,8
|
33,9
|
12,3
|
11,0
|
9,54
|
23 |
41,6
|
38,1
|
35,2
|
13,1
|
11,7
|
10,2
|
24
|
43,0
|
39,4
|
36,4
|
13,8
|
12,4
|
10,9
|
25
|
44,3
|
40,6
|
37,7
|
14,6
|
13,1
|
11,5
|
26
|
45,6
|
41,9
|
38,9
|
15,4
|
13,8
|
12,2
|
27 |
47,0
|
43,2
|
40,1
|
16,2
|
14,6
|
12,9
|
28
|
48,3
|
44,5
|
41,3
|
16,9
|
15,3
|
13,6
|
29 49,6
|
49,6 |
45,7
|
42,6 |
17,7 |
16,0
|
14,3
|
30 50,9
|
50,9 |
47,0
|
43,8
|
18,5
|
16,8
|
15,0
|
Подальша процедура цілком зрозуміла.