4.2 Хід роботи

1. Згідно з варіантом введіть у відповідні "вікна" на комп‘ютерній моделі, наприклад, наступні значення коефіцієнтів:

b₀=1; b₁=-3; b₂=2; b₁₁=3; b₁₂=4; b₂₂=-3.

2. Виконайте перші 9 експериментів D-оптимального плану таблиці 1. Експеримент проведіть в точці факторного простору .

Крок варіювання дорівнює ΔХ₁ = ΔХ₂=30.

Вказівка. Для обчислення оцінок потрібно скласти систему нормальних рівнянь, а саме:

,

, (25)

………………………………………………….. ,

,

де

; (26)

; (27)

; (28)

(29)

При N₀=9 система розпадається на чотири частини:

одна - це система рівнянь з 3 невідомими і три - це окремі рівняння з одним невідомим. Це полегшує обчислення. Система має такий же вид після кожного з блоків, відзначених в таблиці 1. Розрахуйте радіус  сфери, що обмежує припустиму область, за формулою

. (30)

4. Визначте координати точки постановки 10-го експерименту.

Для цього порахуйте значення

, i=1, 2, 3, …, 9

і знайдіть точку в якій досягає максимуму.

У випадку, якщо значення для деяких точок співпадають, можна вибрати кожну з них. Порівняйте з точкою 10 в таблиці 1.

5. Виберіть довірчу імовірність Р=0,9 і для неї по таблиці 1 визначте кількість спостережень, які потрібно буде зробити до виконання умови припинення експерименту.

6. Виконайте всі необхідні спостереження і розрахуйте оцінки коефіцієнтів регресії b_k, k=1,2,3, …, 6.

4.3 Формули для розрахунку

1. Радіус області байдужності

.

2. Елементи вектора :

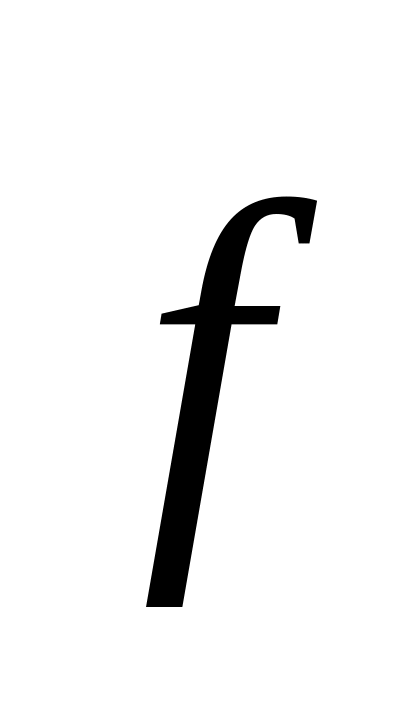3. Елементи матриці

;

;

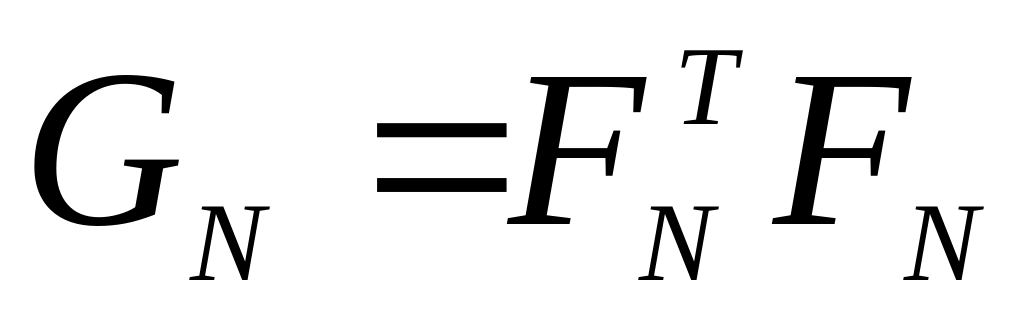
4. Елементи вектора :

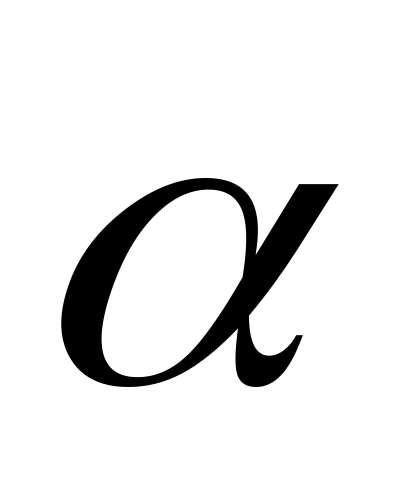, k=0, 1, 2, 3, 4, 5.

5. Система нормальних рівнянь

,

,

,

,

,

6. Дисперсія пророкування функції :

,

де r_jk - елементи зворотної матриці (коваріаційної матриці оцінок) (F^TF)^-1.

Елементи зворотньої матриці r_jk знаходяться по формулі

,

де _jk - алгебраїчне доповнення елемента k-го рядка і j-го стовпця;

 - детермінант (визначник) матриці.

Зауваження.

Обчислення істотно спрощуються, якщо проводити спостереження по блоках, відзначених в таблиці 1. Тоді система нормальних рівнянь має вид:

,

С₁₁b₁=₁;

С₂₂b₂=₂;

С₄₄b₄=₄.

Контрольні питання

1. Дайте визначення D-оптимального плану і перерахуйте його основні властивості.

2. Чим відрізняються точні і безперервні плани?,

3. З яких розумінь визначається кількість спостережень, які необхідно буде провести по D-оптимальному плану?

4. Як вибирається точка проведення наступного експерименту?

5. Як визначаються границі припинення послідовної процедури експерименту?

Література

1. Основи наукових досліджень та технічної творчості: Навч. посібник / Журахівський А.В., Варецький Ю.В., Бахор З.М.; За редакцією І.В. Жежеленка. - Видавництво Приазовського Державного технічного університету, 2000. - 138 с.

2. Проведение научных исследований и педагогический процесс. Филиппов Л.И. М.: Моск. энерг. ин-т, 1987. - 86 с.

2. Шейко В.О., Кушнаренко М.В. Організація та методика науково-

дослідної роботи. К. Техніка. 2002. - 362 с.

4. Смирнов Н. В., Дунин-Барковский И.Н. Курс теории вероятностей и математической статистики. - М.: Наука, 1965.

2. Шторм Р., Теория вероятностей. Математическая статистика. Статистический контроль качества. - М.: Мир, 1970.

3. ГОСТ 15894-70. Статистическое регулирование технологических процессов. М.: 1972.

4. Зажигаев Л.С., Кишьян А.А., Романиков Ю.И. Методы планирования и обработки результатов физического эксперимента. М.: Атомиздат, 1978, - с. 232.

5. Круг Г.К. Теоретические основы планирования экспериментальных исследований. М.: Из-во МЭИ, 1974, - с.185.

6. Боженко Л.І., Гутта О.Й. Управління якістю, основи стандартизації та сертифікації продукції. Навчальний посібник. - Львів, 2001. - 176 с.

7. Новиков В.М., Коцюба А.М. Основи метрології та метрологічна діяльність. Частина 2. Навчальний посібник. - Київ: Нора-прінт, 2001. - 210 с.

8. Объем и нормы испытаний электрооборудования / Под общ. ред. Б.А. Алексеева. Ф.Л. Когана, Л.Г. Мамикоянца. - 6 - е изд.. с изм. и доп. - м.: Изд-во НЦ ЭНАС. 2001. -256 с.

9. Смирнов Н.В., Дунин-Барковский И.В., Краткий курс математической статистики для технических приложений. - М.: ФМ, 1959.

10. Митропольский А.К., Техника статистических вычислений. М., Наука, 1971.

11. Хальд А., Математическая статистика с техническими

приложениями. М., ИЛ, 1956.

12. Налимов Н. В., Чернова Н. Л, Статистические методы плани­рования экстремальных экспериментов, Наука, М, 1965.

13. К р а м е р Г., Математические методы статистики, ИЛ, М., 1948.

14. Голикова Т. И., Микешина Н. Г, Свойство D-оптимальных планов и методы их построения, в кн. "Новые идеи в планировании экспе­римента", Наука, М., 1969.

15. Вучков И. Н., Круг Г. К., D-оптимальные экспериментальные планы, Проблемы планирования эксперимента, Наука, М., 1969.

16. Соколов С. Н. Непрерывное планирование регрессионных

экспериментов. Теория вероятностей и ее применения, том 8, 1963.

Навчальне видання

П.Д. Лежнюк, О. Є. Рубаненко, Ю.В. Лук’яненко