
- •Основи теорії планування експерименту
- •1 Лабораторна робота № 1 метод контрольних меж
- •1.1 Теоретичні відомості
- •1.1.1 Загальні відомості
- •1.1.2 Коротка історична довідка
- •1.1.3 Невизначеність вимірів
- •1.1.4 Стандартна невизначеність
- •1.1.5 Аналіз результатів повторних спостережень
- •1.1.6 Перевірка гіпотези про вид закону розподілу результатів
- •1.1.7 Методи перевірки гіпотез про вид закону розподілу
- •1.1.7.1 Критерій 2 Пірсона.
- •1.1.7.2 Складений критерій
- •1.1.7.3 Обробка результатів кількох серій вимірювань
- •1.1.8 Вимірювання невипадкових величин та їх реалізацій Призначення контрольних меж. Рівноточні виміри постійного величини
- •1.1.9 Статистична характеристика якості продукції
- •1.1.10 Статистичний контроль якості продукції
- •1.1.11 Техніка контрольних карт
- •1.1.12 Форма контрольної карти типу "середнє-размах"
- •1.2 Хід роботи
- •1.3 Приклад виконання завдання
- •1.3.1 Завдання
- •1.3.2 Рішення задачі
- •1.4 Варіанти завдань
- •1.5 Контрольні питання
- •2 Лабораторна робота № 2 однофакторний дисперсійний аналіз
- •2.1 Теоретичний опис роботи
- •2.1.1 Постановка задачі
- •2.1.2 Постановка задачі в загальному вигляді
- •Припущення, на яких базується дисперсійний аналіз
- •2.1.4 Ідея дисперсійного аналізу
- •Однофакторний аналіз
- •2.1.6 Розкладання сум квадратів
- •2.1.7 Оцінка дисперсій
- •2.1.8 Оцінка впливу фактора
- •2.1.9 Випадок нерівнокількісних спостережень
- •2.1.10 Розрахункові формули для суми
- •2.2 Хід роботи
- •2.3 Приклад виконання завдання
- •2.3.1 Завдання
- •2.3.2 Рішення задачі
- •2.4 Варіанти завдань
- •3 Лабораторна робота № 3 багатофакторний дисперсійний аналіз
- •3.1 Теоретичний опис роботи
- •3.1.1 Постановка задачі
- •3.1.2 Розклад сум квадратів
- •3.1.3 Оцінка дисперсій
- •3.1.4. Оцінка впливу факторів
- •3.1.5 Розрахункові формули для сум
- •3.1.6. Опорна стрижнева парцелянова ізоляція
- •3.2 Хід роботи
- •3.3 Приклад виконання завдання
- •3.3.1 Завдання
- •3.3.2 Рішення задачі
- •3.4 Варіанти завдань
- •4 Лабораторна робота № 4
- •4.1 Теоретичні відомості
- •4.2 Хід роботи
- •4.3 Формули для розрахунку
- •Література
- •Основи науково-дослідної роботи
- •21021, М. Вінниця, Хмельницьке шосе, 95 , внту
- •21021, М. Вінниця, Хмельницьке шосе, 95 , внту
2.1.9 Випадок нерівнокількісних спостережень
Вище ми розглянули випадок тільки рівнокількісних серій спостережень на всіх рівнях фактора x. Ця обставина не важлива для теорії дисперсійного аналізу, а тому (при різній кількості mj паралельних спостережень на різноманітних j-х рівнях) схема проведення та основні прийоми аналізу залишаються такими самими. Змінюється лише вигляд наступних виразів:
1) загальна кількість спостережень
![]() (30)
(30)
2) результати спостережень по серіях
![]() (31)
(31)
3) середнє серії
![]() (32)
(32)
4) загальне середнє
![]() (33)
(33)
5) співвідношення для сум
![]() (34)
(34)
6) співвідношення для кількості ступенів свободи
![]() (35)
(35)
7) дисперсія фактора x обчислюється при значному впливі фактора за формулою
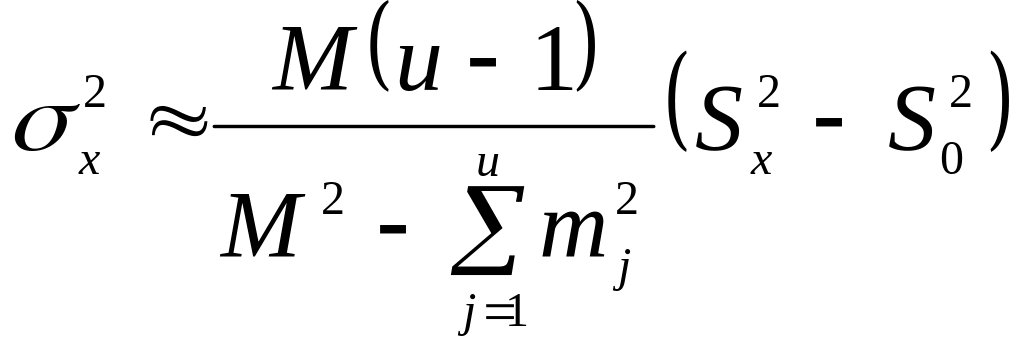 . (36)
. (36)
2.1.10 Розрахункові формули для суми
Обчислювальний алгоритм однофакторного дисперсійного аналізу спрощується, якщо для розрахунку сум квадратів відхилень використовувати перетворення
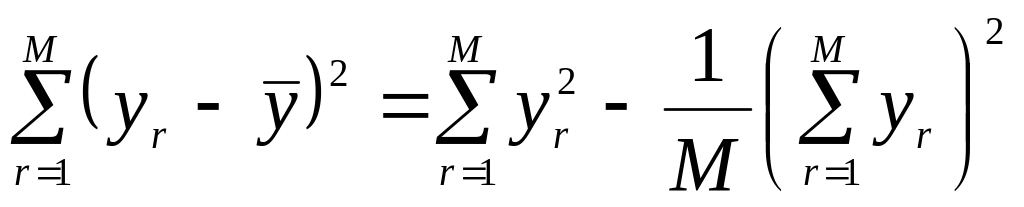 . (37)
. (37)
Тоді для сум отримуємо зручні розрахункові формули:
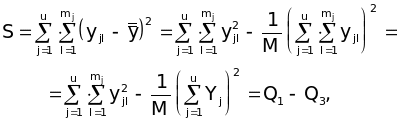 (38)
(38)
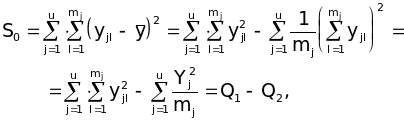 (39)
(39)
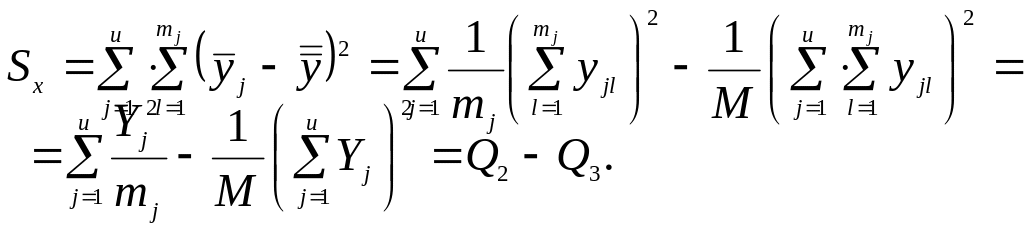 (40)
(40)
Таким чином, для проведення дисперсійного аналізу досить зробити наступні попередні обчислення:
1) підсумки спостережень по серіях
(41)
2) сума квадратів усіх спостережень
![]() (42)
(42)
3) сума квадратів підсумків по серіях, поділена на кількість спостережень в серії
![]() (43)
(43)
4) квадрат загального підсумку, поділений на кількість всіх спостережень
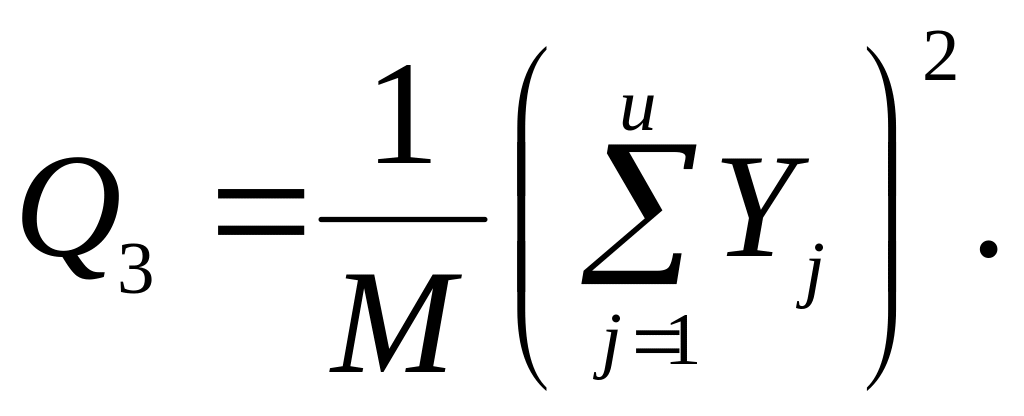 (44)
(44)
2.2 Хід роботи
1. Ознайомтеся з описом комп‘ютерної моделі генератора результатів вимірів.
2. Перепишіть початкові дані у відповідності з номером вашого варіанта.
3. За допомогою комп‘ютерної моделі побудуйте модель виміру параметра y.
Кожне виміряне значення yjl імітує значення виміряного параметра y для l-го елемента (наприклад зразка продукції) в j - ій серії вимірів (або в відібраній j -ій серії виробів) в умовах відсутності систематичної похибки.
4. Запишіть результати вимірів, отримані за допомогою ком‘ютерної
моделі.
5. На основі розрахунків перевірьте значимість впливу досліджуваного
фактора х.
6. Зробіть висновки.
2.3 Приклад виконання завдання
2.3.1 Завдання
Дослідіть, чи залежить довговічність y (вимірюється у годинах) електричних ламп від технології і матеріалу виготовлення (фактор x). Припустимо, що виконуються допущення дисперсійного аналізу, тобто довговічність має нормальний розподіл і вплив роду матеріалу і технології виготовлення електричних ламп не має впливу на дисперсію 2 величини y, але викликає розбіжність середніх значень. Були відібрані нерівнокількісні серії зразків з чотирьох партій (номер партії деталей j змінюється від 1 до u) продукції (u = 4).
Номер лампи в кожній партії l змінюється від 1 до m. Результати спостережень наведені в таблиці 3, причому для спрощення обчислень усі дані зменшені на одну і ту саму величину (1500 годин), тому що на значення дисперсій це не впливає. Підрахунки, що виконані в тієї ж таблиці, зрозумілі без пояснень і необхідні для знаходження суми квадратів відхилень і вибіркових дисперсій.
