2.1.7 Оцінка дисперсій

Припустимо, що вплив фактора x на вихідний параметр буде відсутній, тобто нуль-гіпотеза про однорідність вірна. Тоді всі серії паралельних спостережень можна розглядати як випадкові вибірки з однієї і тієї ж нормальної сукупності і, адже:

1) не зміщена загальна оцінка дисперсій відновлення ² по всім u·m спостереженням визначається за виразом

(12)

з кількістю ступеней свободи

2) вибіркова дисперсія розсіювання «в середині серій», або залишкова оцінка дисперсії відновлення ² знаходиться як середнє з вибіркових дисперсій по кожній серії окремо

(13)

з кількістю ступеней свободи

3) вибіркова дисперсія розсіювання між середніми серій є не зміщеною оцінкою дисперсії , з якою нормально розподілені незалежні одна від іншої середні серій:

(14)

з кількістю ступеней свободи

Звідси легко одержуємо третю оцінку дисперсії відновлення, вибіркову дисперсію розсіювання «між серіями»:

(15)

з кількістю ступеней свободи

Кількість ступеней свободи перевіряється по співвідношенню

4) В результаті більш глибокого аналізу можна довезти, що S₀ і S_x незалежні один від іншого. Зі сказаного очевидно, що через відсутність впливу фактора x вибіркові оцінки S², і S_x однорідні, тому що є оцінками однієї і тієї ж генеральної дисперсії ².

Припустимо тепер, що вплив фактора x на вихідний параметр істотний, тобто нуль-гіпотеза про однорідність вірна. Тоді серії паралельних спостережень можна розглядати як випадкові вибірки u незалежних нормально розподілених випадкових величин з однієї і тією же дисперсією (² і різними центрами розподілу і, адже:

1) вибіркова дисперсія s² характеризує вплив як фактора випадковості, так і фактора x, тобто

(16)

2) оскільки сума S₀ не змінюється при заміні на то вибіркова дисперсія також не змінюється і так само є не зміщеною оцінкою для ², тобто

(17)

3) оскільки сума S_x враховує не тільки випадкові, але і систематичні розходження між середніми серій і збільшується за рахунок впливу фактора x, то дисперсія при цьому також збільшується і перестає бути оцінкою тільки для , тобто

Тому легко одержуємо

(18)

4) незалежність S₀ і S_x один від іншого зберігається.

Таким чином, для дисперсії фактора x тепер можна дати дві приблизних оцінки

(19)

(20)

Перша оцінка менш точна через похибки величин S² і . Точність другої вище, тому що дисперсії, які входять в неї, поділені на m.

Виходячи з другого припущення зрозуміло, що при впливі фактора x вибіркові оцінки S², , S_x неоднорідні. Отже, зіставляючи ці вибіркові дисперсії, можна прийняти рішення про справедливість першого або другого припущення щодо значимості впливу фактора x (з дисперсією ) на вихідний параметр. З огляду на точність виразів (19), (20), для оцінки будемо порівнювати дисперсії і .

2.1.8 Оцінка впливу фактора

Для того щоб вплив фактора x був значним необхідно і досить, щоб дисперсія значно відрізнялася від . Перевірку нуль-гіпотези про однорідність цих вибіркових оцінок можна здійснити за допомогою критерію

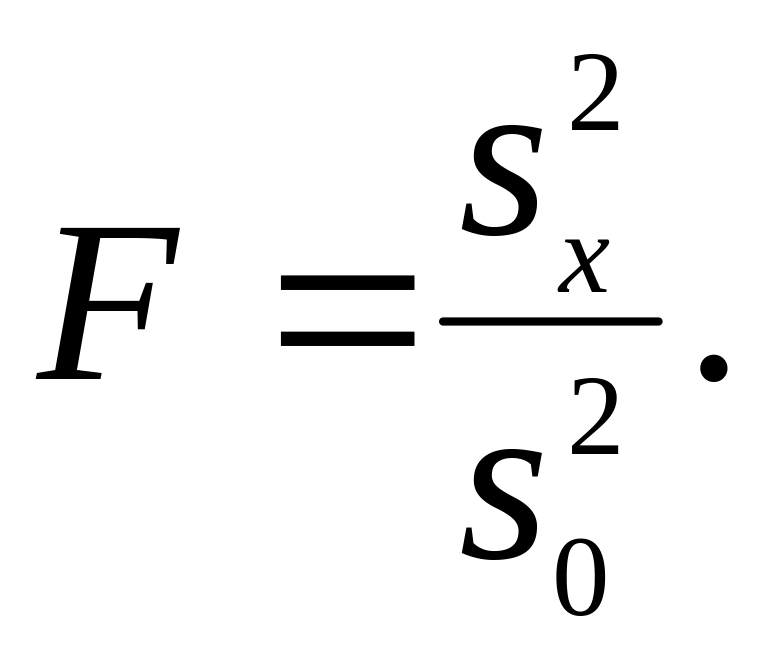(21)

Якщо обчислене за результатами спостережень дисперсійне відношення F переважає табличне F_q(_x, ₀₎ за розподілом Фішера, для обраного рівня значимості q при відповідних ступенях свободи _x і ₀, то вплив фактора x визнається значним , і навпаки - незначним , якщо

В дисперсійному аналізі перевіряють нуль-гіпотезу при альтернативі тому користуються одностороннім F-критерієм. При цьому звичайно вибирають рівень значимості q = 0,05. Варто мати на увазі, що дисперсійний аналіз спостережень експерименту дозволяє визначати вплив фактора лише в цілому, не даючи кількісних оцінок цього впливу. Також варто пам‘ятати, що висновки, отримані з його допомогою, відносяться лише до даного звітного матеріалу, при даній його систематизації. Так, наприклад, при зміні діапазону варіювання досліджуваного фактора х, оцінка впливу х буде мінятися.

Якщо вплив фактора x вважається незначним, то дисперсію відновлення ² можна оцінити вибірковою загальною дисперсією S², що має на u-1 ступінь свободи більше, ніж . Якщо ж вплив фактора x вважається значним, то за результатами спостережень можна оцінити:

1) дисперсію відновлення ² вибіркової залишкової дисперсії

тобто (22)

і визначити довірчий інтервал для ² за -розподілом з u·(m-1) ступенями свободи,

2) дисперсію фактора x за формулою

(23)

3) розбіжність центрів серій, обумовлену впливом фактора x. Оскільки

(24)

то можна показати, що

(25)

де

і тоді

(26)

Оцінкою величини буде вибіркова характеристика

(27)

4) розбіжність між центрами будь-яких двох серій тому, що параметр

(28)

відповідає розподілу Ст‘юдента з кількістю ступенів свободи

то інтервал

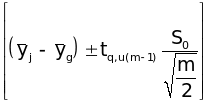(29)

буде довірчим (1-q)% інтервалом для .