1.1.11 Техніка контрольних карт

Для полегшення процедури статистичного регулювання якості продукції в умовах виробництва використовується техніка контрольних карт. Існує кілька типів контрольних карт:

• карта середніх значень ("карта "),

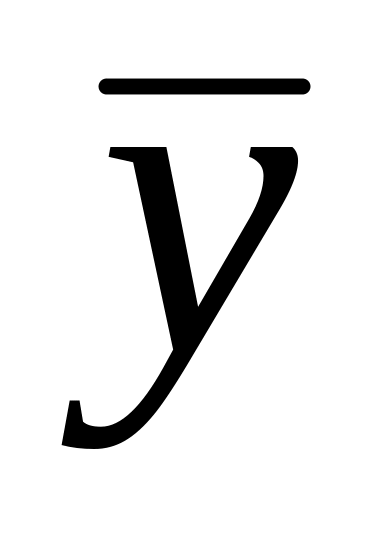• карта медіан ("карта "),

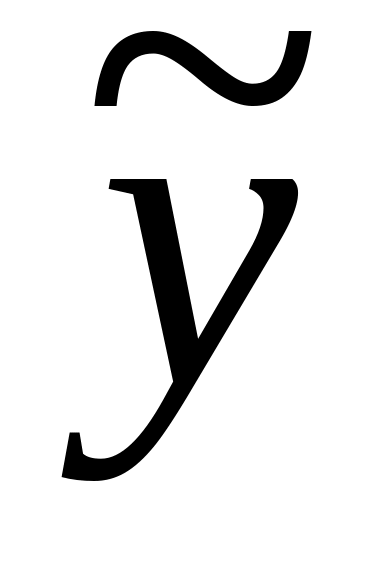• карта середньоквадратичних відхилень ("карта "),

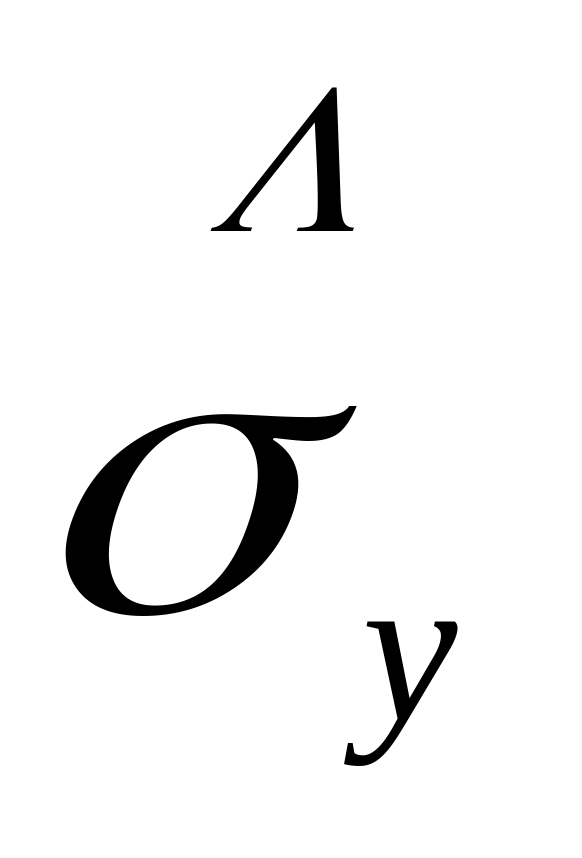• карта розмахів ("карта 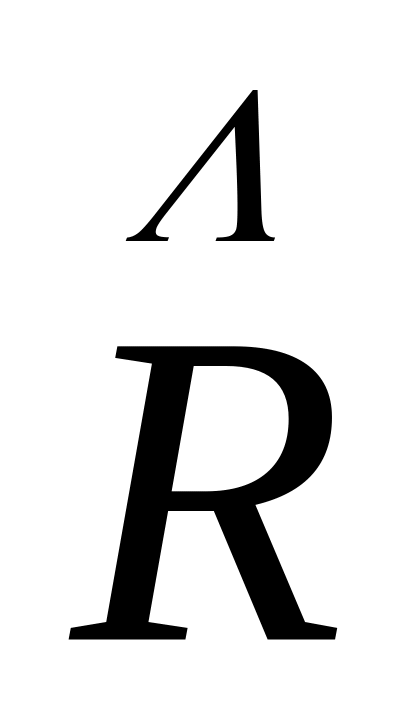") і ряд комбінованих карт, наприклад, "карта / ", "карта 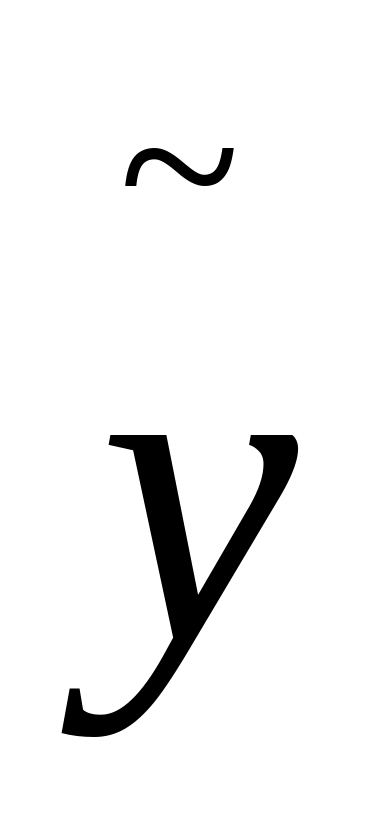/ 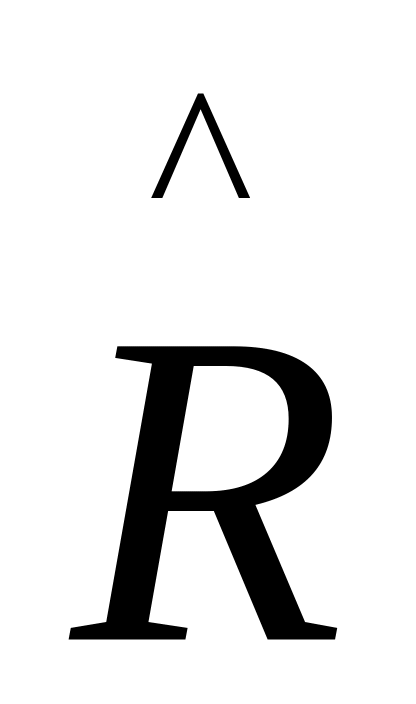" і т.п. [2].

На контрольній карті середніх значень ("карта ") по вісі ординат відзначаються верхня і нижня границі. Посередині між і проводиться вісь абсцис, на якій через різні відрізки відзначаються моменти відбору проб і = 1, 2, ... . Значення для кожної проби наносяться на карту. Границі і розраховані так, що область значень між границями відповідає області прийняття гіпотези . Якщо ж > або < , то гіпотеза відкидається, і, тому, потрібна зупинка виробничого процесу.

Аналогічно будується карта середньоквадратичних відхилень ("карта "). Вихід розрахункового значення ( за верхню границю означає, що гіпотеза відкидається, і, виходить, точність технологічної системи погіршилася. Потрібна зупинка процесу й аналіз причин розлагодження. За нижню границю границя на "карті " беруть нульове значення.

Оскільки підрахунок середньоквадратичного відхилення за формулою 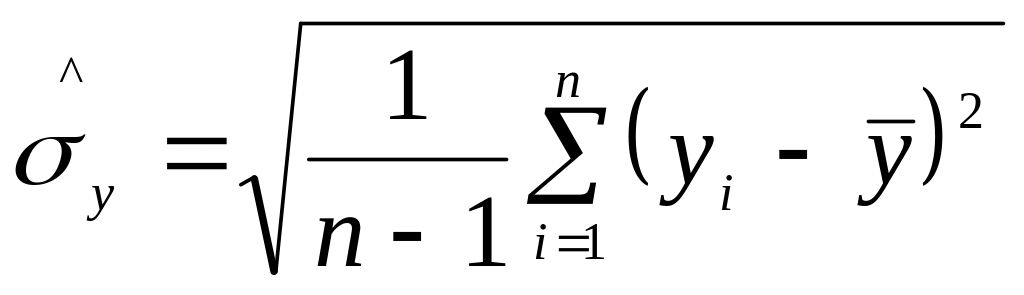для виробничих умов досить складний, замість "карти " зазвичай використовують карту розмахів ("карта "), для якої як вибірковий розмах R_i використовують різницю між найбільшим і найменшим значеннями показника якості в пробі:

R_i = y_{i max} - y_{i min}. (47)

Гіпотеза відкидається, якщо

В роботі розглядається техніка побудови і ведення карти, що найбільше застосовується: комбінованої карти «середнє — розмах». Зі співвідношення (36) легко одержати формули для розрахунку верхніх і нижніх границь карти середніх:

(48)

де - квантіль нормованого нормального закону розподілу (знаходиться по таблиці для різних Р = , n- загальна кількість вимірів.

У випадку, якщо невідомі значення номіналу y₀ і величини ², використовують їхню оцінку і , отримані в результаті спеціально організованих досліджень. Тоді формула (38) приймає вигляд

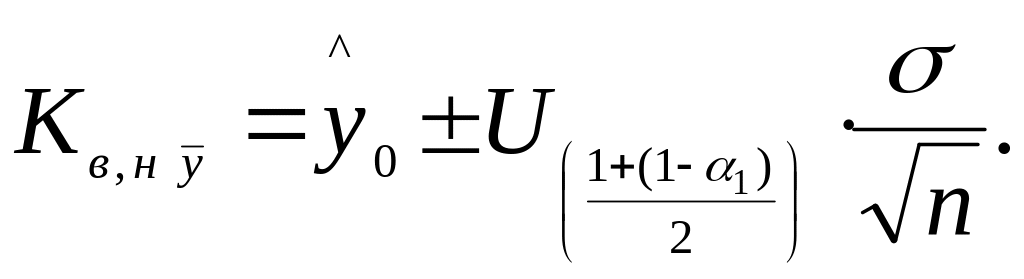(49)

Виведення формули для розрахунку границі що визначає область прийняття гіпотези , базується на законі розподілу вибіркової функції [2] і відомим в статистиці співвідношенням де d - деяке постійна, що залежить від об‘єму вибірки n. Пропускаючи виведення формули для наведемо її кінцевий вигляд:

(50)

де d₀ - табличне значення коефіцієнта, що залежить від об‘єму проби n і обраного рівня значимості . З формул (38), (39) і (40) випливає, що для розрахунку границь комбінованої "карти / " необхідно знати наступні параметри:

• y₀ - номінальне значення показника якості або його оцінку ;

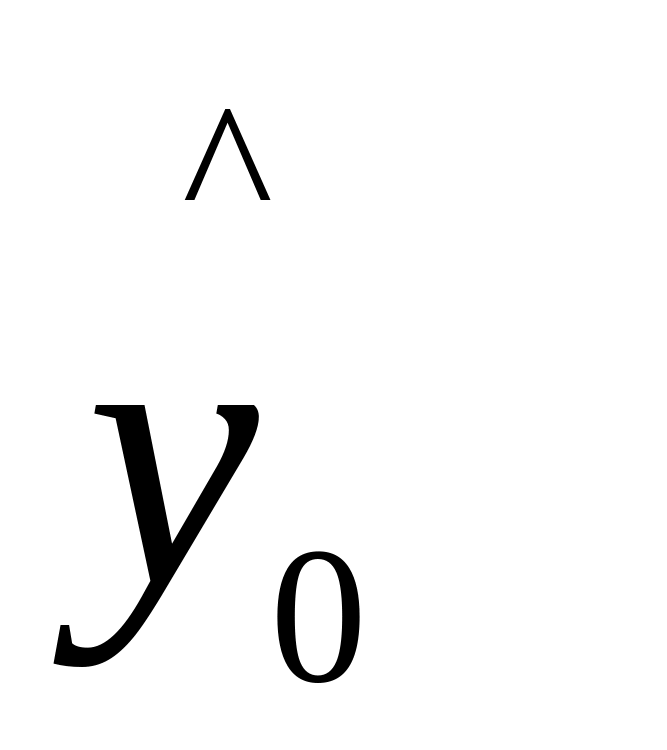• ² - характеристику точності роботи технологічної системи або її оцінку 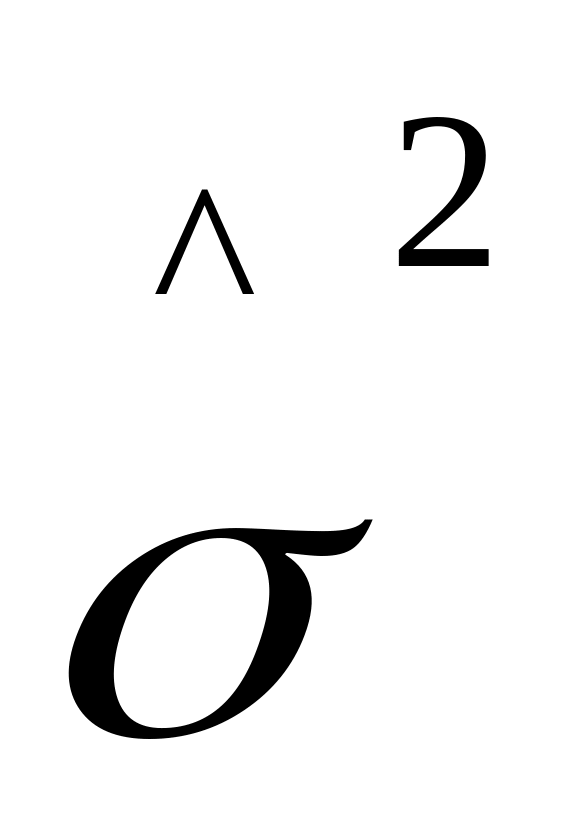, знайдену через оцінку розмаху ;

• - оцінку розмаху;

• n - кількість вимірів показника якості, що містяться в пробі;

• ₁ - рівень значимості для перевірки гіпотези ;

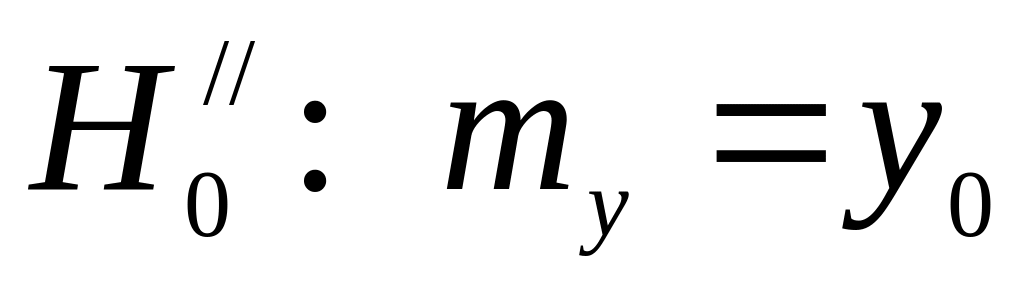• ₂ - рівень значимості для перевірки гіпотези ;

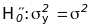• d₀ - табличне значення для коефіцієнта.

Значення перших трьох параметрів або задаються, або визначаються на підставі даних спеціальних попередніх досліджень технологічного процесу. Останні чотири параметри вибираються відповідно до рекомендацій ГОСТ 15894-70 «Статистичне регулювання технологічних процесів» [3]. Згідно ГОСТ ₁ = 0,0027, що відповідає 3-м довірчим межам; ₂ = 0,012, що відповідає 2,5 -м довірчим межам. Значення n береться в границях 3-10 у залежності від продуктивності, стабільності й інших технологічних факторів. У процесі статистичного контролю обране значення n залишається незмінним. Значення коефіцієнта d₀ при ₂ = 0,012 і обраному значенні n визначається по таблиці 6 [2]:

Інтервал часу t між відборами проб також залежить від продуктивності технологічного процесу, від тривалості циклу між двома розлагодженнями процесу і т.д. Практично t беруть в межах 1-2 години. На практиці справжні значення y₀ і ², як правило, невідомі, і необхідно одержати їх оцінки. Для цього на технологічному процесі проводять так назване «попереднє дослідження». В результаті такого дослідження одержують вибірку, що містить n₀ = 100-150 значень показника якості (а іншими словами - вимірюваного параметра) y. Вибірку n₀ набирають у вигляді сукупностей проб, наприклад, якщо вибрано n = 5, то число проб Для отримання оцінки (для будь-якої g-ї проби) обчислюється середнє значення.

Таблиця 6 - Значення коефіцієнта d₀ при ₂ = 0,012

n	3	4	5	6	7	8	9	10
d0	2,35	2,10	1,86	1,79	1,74	1,74	1,70	1,67

(51)

Оцінку y₀ отримуємо як середнє арифметичне m середніх значень по окремих пробах

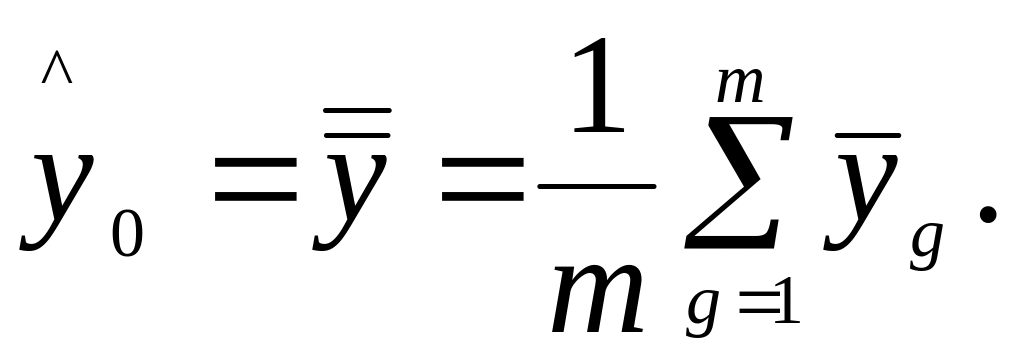(52)

Для знаходження оцінки в кожній g-й пробі визначається розмах

R_g = y_gmax - y_gmin, g = 1, ..., m, (53)

після цього обчислюється оцінка розмаху для генеральної сукупності, як усереднене значення розмахів по окремих пробах

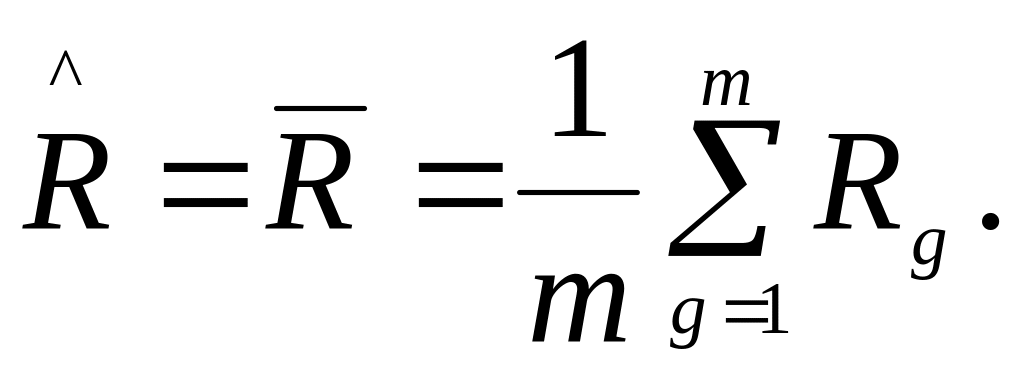(54)

Оскільки відомо [2], що , то незрушена оцінка для має вигляд

(55)

де значення коефіцієнта d залежить від об‘єму n проби і визначається по таблиці 6 [2].

Таблиця 7 - Значення коефіцієнта d

n	3	4	5	6	7	8	9	10
d	1,70	2,06	2,33	3,53	2,70	2,85	2,97	3,08

Використовуючи дані попередніх досліджень (43), (44) і (45), за формулами (51) і (52) розраховують попередні контрольні границі , , , що наносяться на діаграму (рисунок 5). На вісі абсцис через рівні проміжки позначаються порядкові номери проб, відібраних у попередніх дослідженнях. Далі на діаграму наносяться значення всіх і . Якщо деякі значення або виходять за розраховані контрольні границі, то відповідні їм проби виключаються з даних попередніх досліджень (наприклад, на мал. 3 проби 10 і 17), після чого перераховуються оцінки і відповідно виправляються контрольні границі. Це пояснюється тим, що оцінки і контрольні границі повинні відповідати нормальному, стабільному ходові технологічного процесу.