8

Одесская национальная академия связи им. А.С. Попова Кафедра теории электрической связи им. А.Г. Зюко

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к выполнению

индивидуального задания по дисциплине

«ОСНОВЫ ТЕОРИИ ЦЕПЕЙ, СИГНАЛОВ И ПРОЦЕССОВ

В СИСТЕМАХ ТЕХНИЧЕСКОЙ ЗАЩИТЫ ИНФОРМАЦИИ»

на тему

«ОПИСАНИЕ СИГНАЛОВ ЭЛЕКТРОСВЯЗИ

и РАСЧЕТЫ ИХ ХАРАКТЕРИСТИК»

Составители: Иващенко П. В.

Орябинская О.А.

Одесса 2013

Общие сведения

Индивидуальное задание (ИЗ) выполняют студенты, обучающиеся по направлению «Системы технической защиты информации»; при изучении дисциплины «Основы теории цепей, сигналов и процессов в системах технической защиты информации». Студент выполняет ИЗ по варианту, номер которого совпадает с порядковым номером фамилии студента в журнале академической группы.

Конкретные исходные данные для заданного номера варианта студент выписывает из Приложения А этих указаний. Согласно указанному преподавателем сроку выполнения отдельных задач студент должен представить руководителю для просмотра материалы с решением задач. Работу студента над ИЗ руководитель учитывает при ежемесячных аттестациях текущей работы.

Студент оформляет выполненное ИЗ согласно правилам оформления текстовых документов (Приложения Д, Е). Все графики строятся с использованием числовых масштабов по осям координат.

Оформленное ИЗ студент сдает руководителю на рецензирование и, после положительной рецензии, защищает его. Зачтенное ИЗ вместе с зачтенными практическими и лабораторными занятиями является условием допуска студента к экзамену по модулю.

ИЗ состоит из трех задач.

Задача 1. Расчет спектральных характеристик импульсного сигнала

Импульсный сигнал s(t) задан аналитическим выражением, определяющим его форму. Это может быть импульс: ГАУССОВСКИЙ, ДВУСТОРОННИЙ ЭКСПОНЕНЦИАЛЬНЫЙ, ТРЕУГОЛЬНЫЙ, КОСИНУС, КОСИНУС-КВАДРАТ или ПОДНЯТЫЙ КОСИНУС. Заданы также два числа: A (мВ), определяющее амплитуду импульса, и b (мc), определяющее скорость изменения сигнала. Необходимо:

1. Рассчитать и построить график сигнала s(t), определить его длительность.

2. Найти выражение для спектральной плотности сигнала S(j). Построить график амплитудного спектра S(f)= |S(j2f)| для области значений f  0.

3. Определить ширину спектра сигнала F_max, как протяжность интервала (0, F_max), вне которого нормированные значения амплитудного спектра S(f)/ S(0) не превышают заданное значение y.

Указания к решению задачи 1

Задача 1 относится к разделу “Спектральный анализ непериодических сигналов с помощью преобразования Фурье”. Cведения о спектральном представлении непериодических сигналов приведены в литературе [1, разд. 2.6].

Расчет и построение графика заданного сигнала s(t)

Общий вид сигналов, которые встречаются при выполнении ИЗ, показан в Приложении Б. Необходимо построить график с использованием числовых масштабов по осям координат. Заданная функция s(t) четная, поэтому для построения графика достаточно рассчитать точки для t  0. При выборе значений переменной t необходимо учитывать скорость изменения заданной функции s(t).

В случае гауссовского и двустороннего экспоненциального импульсов, учитывая, что е⁰ = 1, е^–1 = 0,368; е^–2 = 0,135; е^–3 = 0,050; е^–4 = 0,018, значения t выбирают таким образом, чтобы аргумент экспоненты принимал значения от 0 до 4 с шагом 0,5 или 1.

В случае косинус-импульса и косинус-квадрат импульса значения t выбирают так, чтобы аргумент косинуса принимал значения 0; /8; /4; 3/8; /2. В случае поднятого косинус-импульса – значения 0; /4; /2; 3/4; .

Пример 1. Задан сигнал – степенной импульс

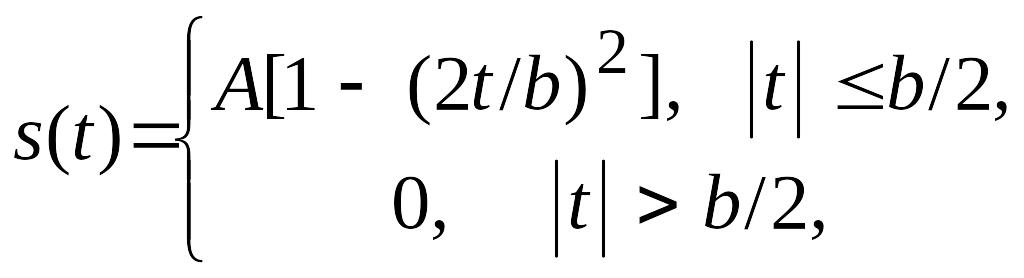
где А = 50 мВ, b = 80 мс.

Из аналитического описания видно, что функция s(t) четная, максимальное значение импульса s(0) = A. При изменении t от 0 до b/2 функция s(t) монотонно убывает, поэтому достаточно рассчитать 2 или 3 промежуточные точки. Результаты расчета представлены в табл. 1.

Таблица 1 – Расчетные значения степенного импульса s(t)

t, мс	0	10	20	30	40
s(t), мВ	50	46,9	37,5	21,9	0

Построенный по точкам табл. 1 график s(t) приведен на рис. 1.

П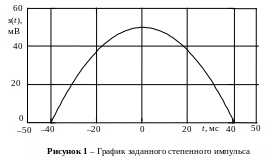 олучение выражения для спектральной плотности заданного сигнала

Поскольку заданный сигнал – функция четная, то целесообразно использовать косинус преобразование Фурье

.

В Приложении Г приведены некоторые соотношения, которые помогут выполнить математические преобразования. Рекомендуется интегрирование выполнить в общем виде, а числовые даны подставить в конечный результат. Для получения конечного выражения нужно перейти к частоте f, выполнив замену  = 2f.

В Приложении В приведены конечные выражения для спектральной плотности S(f), как справочные данные для самопроверки.

Пример 2. Найдем спектральную плотность сигнала, использованного в примере 1.

= 2 А – =

= 2 А – =

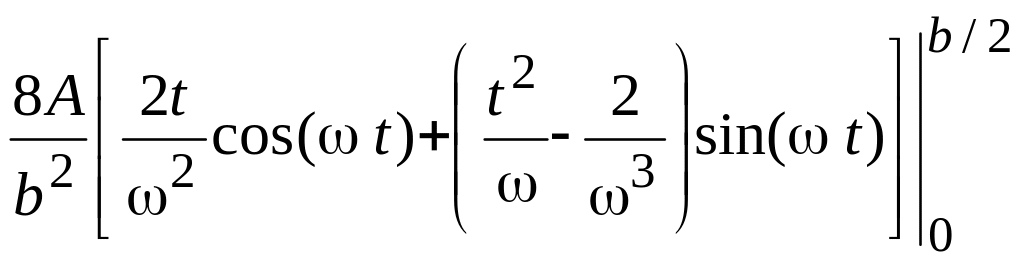= 2 А .

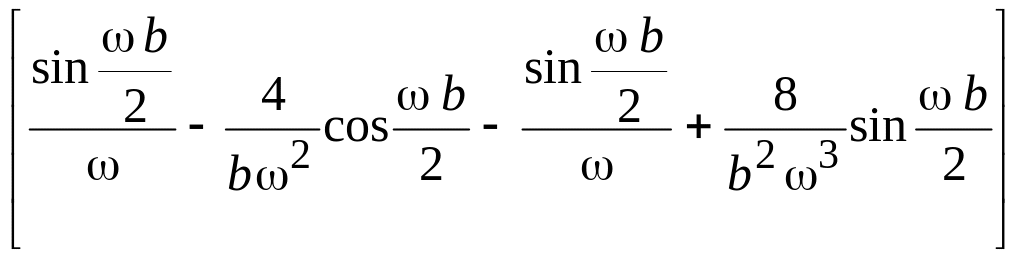Переходя к переменной f, получим окончательное выражение для спектральной плотности

, –   f  .

Построение графика амплитудного спектра

Амплитудный спектр – это модуль спектральной плотности S(f). Для построения графика важно определиться с шагом для переменной f. Для этого можно воспользоваться видом графиков S(f), приведенных в Приложении В. Из этих рисунков видно, что достаточно просчитать значения функции S(f) для области значений f от нуля до 3/b. С учетом скорости изменения функции S(f) шаг для f в 3–4 раза меньше, чем 1/b. Необходимо обязательно найти экстремальные значения функции S(f).

При расчетах значений функций S(f) может появиться неопределенность вида 0/0. Эту неопределенность можно снять по известным математическим правилам. Приведем некоторые из неопределенностей, которые встречаются при выполнении ИЗ. Они раскрываются по правилу Лопиталя

;

;

.

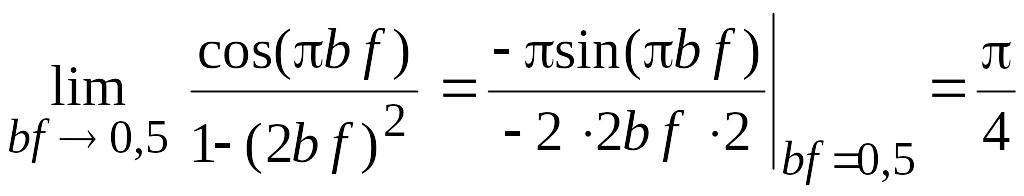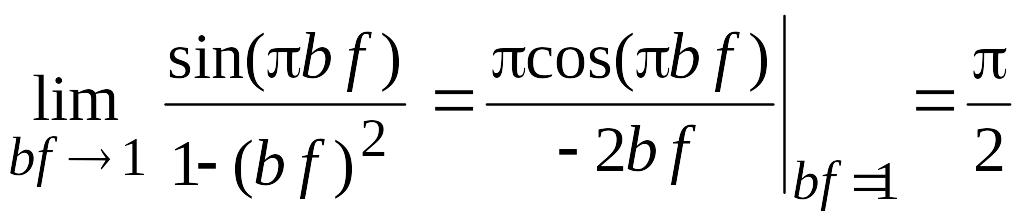Пример 3. Для найденной в примере 2 спектральной плотности построить график амплитудного спектра S(f). При f = 0 имеем неопределенность 0/0. Положим bf = x и раскроем ее

.

Выберем для сложной переменной bf шаг, равный /4, или шаг для f = 1/(4b). Учитывая, что b = 80 мс, в качестве шага для f примем целое число, а именно 4 Гц. Результаты расчетов сведем в табл. 2.

Таблица 2 – Расчет графика амплитудного спектра

f, Гц	0	4	8	12	16	20	24	28	32	36	40
bf	0	1,01	2,01	3,02	4,02	5,03	6,03	7,04	8,04	9,05	10,05
S(f), мВ/Гц	2,67	2,40	1,73	0,91	0,22	0,16	0,22	0,10	0,04	0,09	0,06

Экстремальное значение функции S(f), когда она принимает нулевое значение, имеет место при sin(bf)/(bf) – cos(bf) = 0, или tg(bf) = bf. Подбором на калькуляторе найдем, что первый нуль имеет место при bf₀₁ = 4,5; f₀₁ = 4,5/(b) = 4,5/(0,08) = 17,9 Гц.

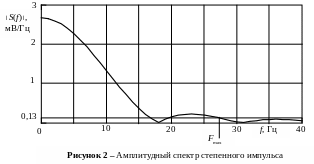
Рассчитанный график S(f) приведен на рис. 2.

Определение максимальной частоты спектра сигнала F_max

Частота F_max определяется по условия, что значения амплитудного спектра на частотах f  F_max не превышают заданное значение y = S(F_max)/S(0). Рекомендуется F_max определить графически, хотя для гауссовского и двустороннего экспоненциального импульсов F_max можно определить аналитически. Итак, на графике S(f) необходимо указать значение S(F_max) = yS(0), а затем определить значение F_max на пересечении горизонтальной прямой на уровне S(F_max) и графика S(f).

Пример 4. Для спектра, рассчитанного в примере 3, определить F_max при условии, что y = S(F_max) / S(0) = 0,05. Поскольку S(0) = 2,67 мВ/Гц, S(F_max) = 2,670,05 = 0,13 мВ/Гц. На пересечении горизонтальной прямой на уровне 0,13 и графика S(f) (рис. 2) находим, что F_max = 27 Гц.