4. Розклад сигналу за ортогональним та ортонормованим базисами
4.1. Система ортогональних функцій
Перехід
до функціонального простору сигналів,
в якому визначена норма, метрика та
скалярний добуток сигналів, дозволяє
визначити кут між функціями
та
згідно формули:
.
(4.1)
Враховуючи,
що
,
умова ортогональності двох функцій
та
зводиться до виразу:
для комплексних функцій:
;
(4.2)
для дійсних функцій:
.
(4.3)
Значення
скалярного добутку
залежить від інтервалу інтегрування
[a,
b],
на якому він розглядається. Цей інтервал
може бути як скінченим, так і нескінченим.
Ортогональна
система функцій – це така впорядкована
множина функцій
:
скінчена
,
(4.4)
або
нескінчена
(4.5)
в
якій норма будь-якої функції
не дорівнює нулю:
,
(4.6)
а
будь-яка пара функцій
та
ортогональна, тобто
– множина попарно ортогональних функцій,
для яких виконується умова:
для системи комплексних функцій:
.
(4.7)
для системи дійсних функцій:
.
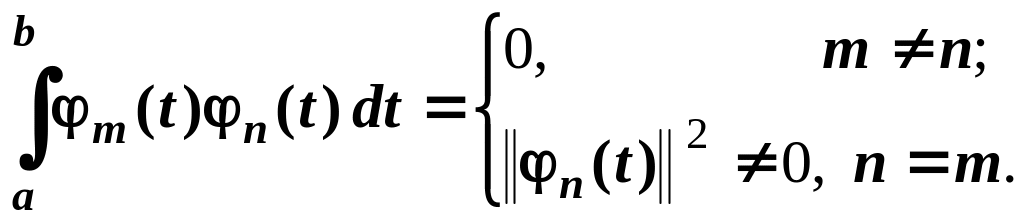(4.8)
4.2. Ортогональне розвинення функцій
Ортогональне розвинення кусково-неперервної функції S(t), інтеграл якої на інтервалі розвинення [a, b] існує:
,
(4.9)
– це апроксимація цієї функції у вигляді ряду за ортогональною системою функцій :
,
(4.10)
де
– коефіцієнт розвинення за вибраною
ортогональною системою функцій
на заданому інтервалі розвинення [a, b].
Вибір системи ортогональних функцій залежить від мети розвинення: потрібна точна чи наближена апроксимація, з допомогою скінченого чи нескінченого ряду, з швидкою чи повільною збіжністю ряду, з застосуванням найпростіших чи спеціальних функцій.
Ортогональне розвинення сигналу S(t) подає його як лінійну комбінацію простих або спеціальних функцій (4.10), що дозволяє вивчати структурні особливості складного сигналу S(t), виходячи з уже відомих властивостей базових функцій . Застосування спеціальних функцій дозволяє забезпечити певні характеристики вихідних сигналів ще на стадії формування вхідних сигналів.
Правильно вибране ортогональне розвинення сигналів суттєво спрощує програмне чи апаратне забезпечення процедур цифрової обробки сигналів.
4.3. Мінімізація середньоквадратичного відхилення ортогонального розвинення функції
Спосіб
обчислення коефіцієнтів
ортогонального розвинення функції
визначається вибраним критерієм точності
апроксимації: вимога мінімуму модуля
відхилення
;
вимога мінімуму середньоквадратичного
відхилення
тощо.
Розглянемо ортогональне розвинення функції обмеженим рядом (4.10):
.
(4.11)
Коефіцієнт визначає вагу кожної базової функції в цьому розкладі.
Визначимо
із умови мінімізації середньоквадратичної
помилки апроксимації
:
.
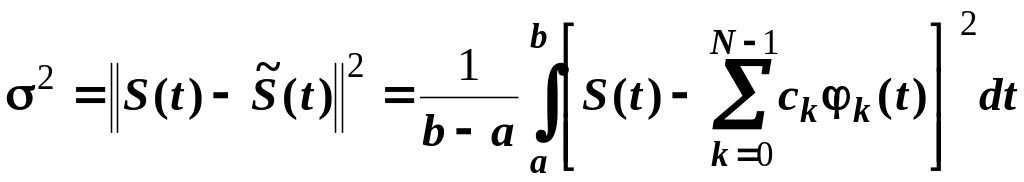(4.12)
Згідно
(4.12)
є функцією коефіцієнтів
,
тому для її мінімізації треба прирівняти
до нуля часткові похідні:
,
k = 0, 1, 2, …, N – 1.
(4.13)
Диференціюючи рівняння (4.12), одержимо
,
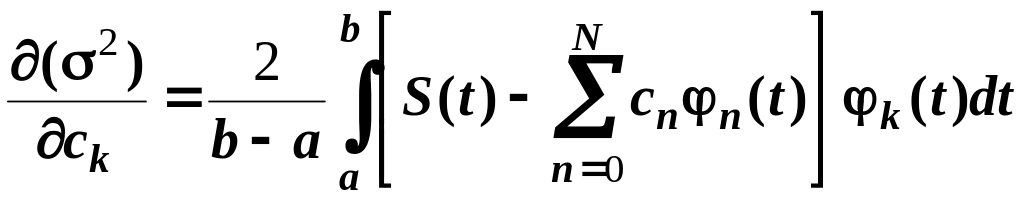k = 0, 1, 2, …, N – 1.
(4.14)
Підставивши (4.14) в (4.13), після простих перетворень одержимо:
.
(4.15)
Так
як система базових функцій
ортогональна, то добуток
при n ≠ k.
Тому (4.15) набуде вигляду
,
(4.16)
звідки
.
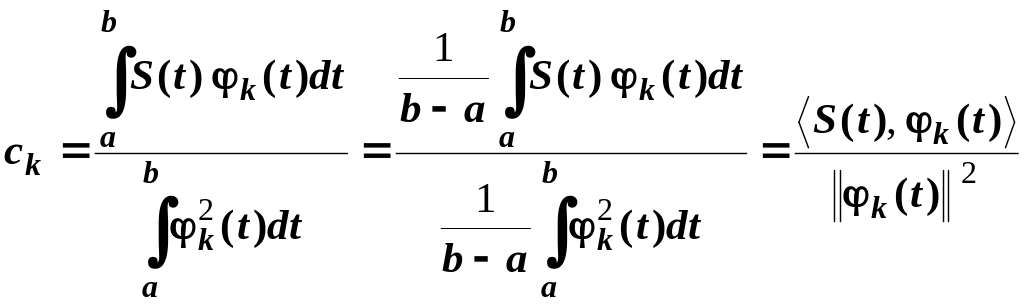(4.17)
Отже, незалежно від того, як визначена норма, міра та відповідний їм скалярний добуток, коефіцієнт відповідає виразу:
,
(4.18)
де
та
− відповідно сумісна енергія та середня
потужність функцій S(t)
та
на інтервалі [a, b];
та
− відповідно енергія та середня
потужність базової функції
на інтервалі [a, b].
Отже, ортогональне розвинення функції S(t) обмеженим рядом (4.10) забезпечує найкращу апроксимацію в розумінні мінімізації середньоквадратичної похибки, якщо коефіцієнти розкладу визначаються за формулою (4.17) чи (4.18).