5. Контрольные вопросы.
1. Что такое пружинный маятник?
2. Под действием каких сил происходят свободные затухающие колебания пружинного маятника?
3. Записать дифференциальное уравнение затухающих колебаний пружинного маятника и его решение.
4. Какой физический смысл имеют и в каких единицах измеряются период колебаний, коэффициент затухания и логарифмический декремент затухания?
5. Назовите параметры пружинного маятника и единицы их измерения.
6. Проанализируйте зависимость характеристик затухающих колебаний параметров пружинного маятника.
6. Приборы и оборудование.
Пружинный маятник со шкалой отсчета, линейка, секундомер, груз.
7. Литература.
Кучерук І.М., Горбачук І.Т., Луцик П.П. Загальний курс фізики. Київ, “Техніка”, 1999.-Т.1, §§10.2, 10.8.
Савельев И.В. Курс общей физики. М. “Наука”, 1982.-Т1, §§50, 58.
Вариант 3 Изучение свободных затухающих колебаний математического маятника
1. Цель работы.
Изучить затухающие колебания математического маятника и определить характеристики затухающих колебаний (период затухающих колебаний, логарифмический декремент затухания, коэффициент затухания, время релаксации колебаний).
2. Теоретические сведения.
В реальных физических системах, осуществляющих свободные колебания, кроме внутренней силы, которая возвращает систему к положению равновесия, всегда действуют силы трения и сопротивления. Поэтому реальные свободные колебания происходят с постепенными потерями энергии колебаний на работу против этих сил и создания колебаний в окружающей среде, и они являются затухающими.
Рассмотрим свободные затухающие колебания математического маятника. Математическим маятником называется материальная точка подвешена на невесомой и нерастяжимой нити, колеблющаяся в вертикальной плоскости под действием силы тяжести. На практике математическим маятником можно считать металлический шарик массой m, подвешенный на легкой нити, длина которой l значительно больше размеров шарика (рис. 1). Центр масс такой системы совпадает с центром масс шарика.
При отклонении маятника от положения равновесия возникает возвращающая к положению равновесия сила F, которая является составляющей силы тяжести шарика и равна:
,
где g – скорение свободного падения, α- угловое смещение маятника относительно положения равновесия. При малых углах (α ≤10º )
,
(1)
где х – линейное смещение шарика относительно положения равновесия.
Поэтому возвращающая сила равна:
,
(2)
где знак "-" указывает на то, что сила направлена в противоположную сторону к смещению х.
Возвращающая
сила F
по природе не
является упругой,
но как и
последняя пропорциональна
смещению
от положения равновесия,
поэтому она называется
квазиупругой.
Коэффициент
называется коэффициентом
квазиупругой
силы.
Будем считать, что причиной затухания колебаний является сила сопротивления вязкой среды, в случае небольшой скорости движения тела равна:
,
(3)
где r – коэффициент сопротивления, зависящий от вязкости среды и формы тела, а – скорость тела равна:
Знак “ - ” в уравнении (3) указывает на то, что сила сопротивления воздуха направлена в сторону противоположную скорости шарики.
Запишем уравнение динамики движения математического маятника:
,
(4)
где а
- ускорение шарика,
которое равно:
П
одставим
выражение для
скорости и ускорения
в формулу
(4) и получим:
Разделим последнее уравнение на m и введем обозначения:
(5)
Окончательно уравнение свободных затухающих колебаний математического маятника будет иметь вид:
(6)
Решением этого уравнения является функция:
(7)
Учитывая то, что угловое смещение α согласно формуле (1) пропорциональное линейном смещению х, дифференциальное уравнение свободных колебаний и его решение можно представить в виде:
(8)
,
где
- амплитуда
затухающих колебаний
в произвольный момент
времени,
- амплитуда колебаний
в начальный момент времени,
β –
коэффициент затухания,
определяется формулой
(5),
- циклическая частота
затухающих колебаний
,
(9)
где
- собственная частота
колебаний:
(10)
Как видно из уравнения затухающих колебаний, амплитуда колебаний со временем уменьшается, поэтому затухающие колебания лишь условно можно считать периодическими. Условный период затухающих колебаний определяется по формуле:
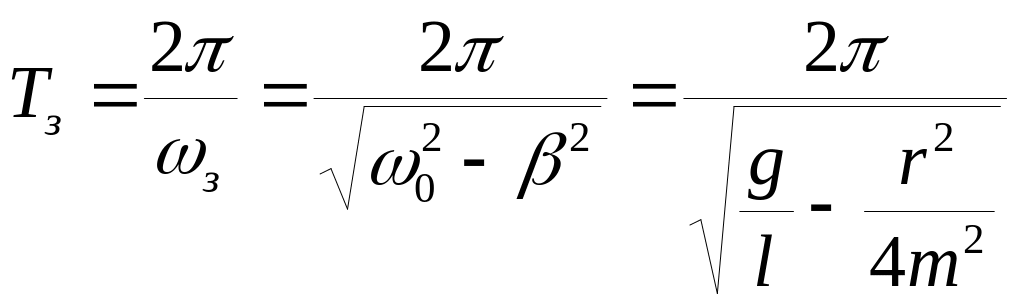(11)
График затухающих колебаний показан на рис. 2.
Рис. 2.
Амплитуда затухающих колебаний уменьшается по экспоненциальному закону, но отношение амплитуд двух последовательных колебаний является величиной постоянной, т.е. характеристикой колебаний. Эта величина называется декрементом затухания, а ее логарифм логарифмическим декрементом затухания:
(12)
Затухающие колебания также характеризуют временем релаксации τ. За это время амплитуда колебаний уменьшается в е раз:
Откуда следует, что:
(13)
Таким образом, частота, период, коэффициент затухания, время релаксации и логарифмический декремент затухания являются характеристиками затухающих колебаний.