10.1. Кривые нагревания проводов при различных коэффициентах изменения сопротивления

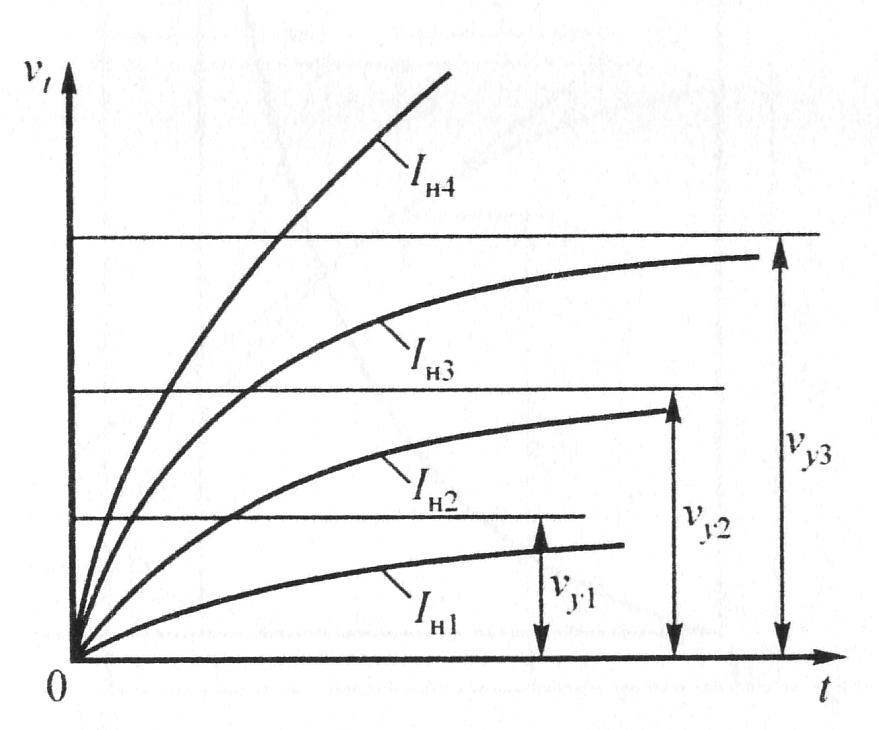
Рис. 10.2. Кривые нагревания проводов при различных токах

В этом случае стремится к бесконечно большому значению. Другими словами, установившегося значения здесь нет, что условно показано на рис. 10.2 (ток I_н4) и на рис. 10.3 (ток I_н). Из выражения (10.18) следует, что установившееся значение достигает бесконечно большого значения при

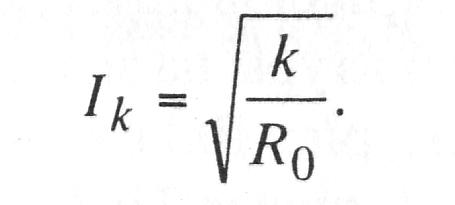(10.20)

Это значение обычно превышает реальные нагрузки на провод. При этом установившееся значение будет нарастать по гиперболе, например, для провода марки МФ-100 с = 0,39 Дж/(кг·К); при С = gγβ = 100·8,91·0,39 = 350 Вт·с/(°С·м); α = 0,004 1/°С, температура перегрева определяется:

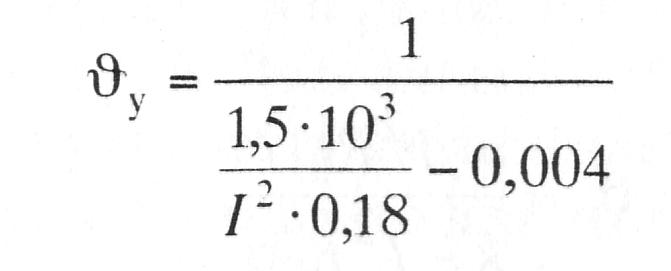
и будет изменяться следующим образом:

I, А ……………………………………….200 400 800 1200 1400

, ºC..……………………………………. 5 25 118 530 ∞

Кривая (t), построенная по уравнению (10.14), имеет экспоненциальный характер (рис. 10.4). Определим на экспоненте длину подкасательной ВС, т. е. длину горизонтальной проекции касательной на участке кривой от точки касания до пере сечения с асимптотой = в точке С.

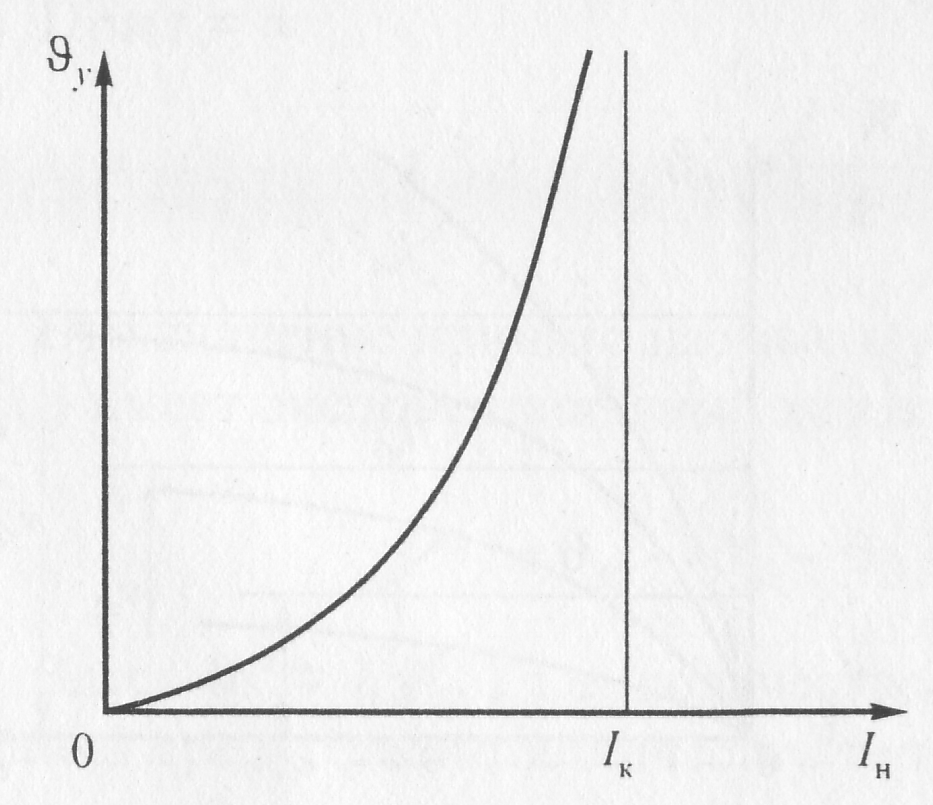
Рис. 10.3. Зависимость установившейся температуры от тока

При α>0

(10.21)

где АВ= - .

Используя выражения (10.14) и (10.18), будем иметь

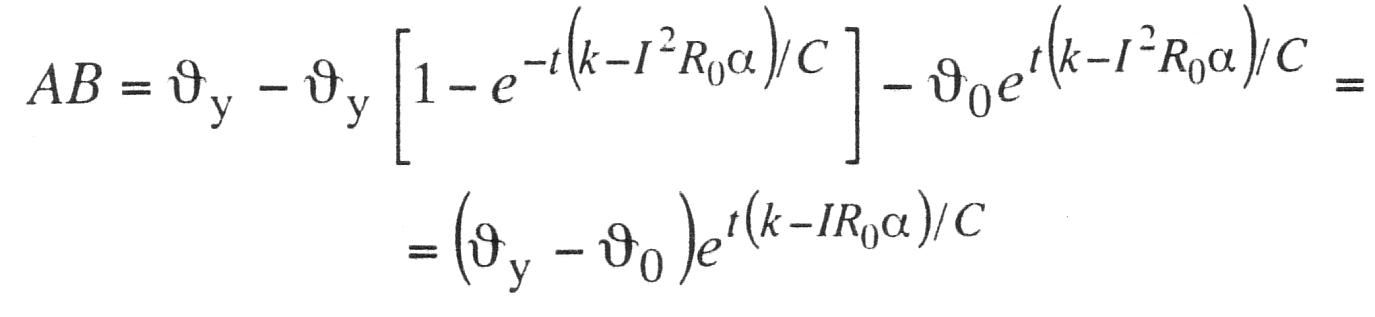(10.22)

и

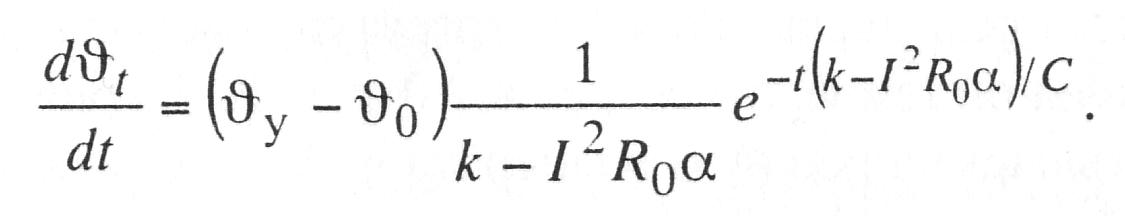(10.23)

Подставив выражения (10.22) и (10.23) в уравнение (10.21), получим

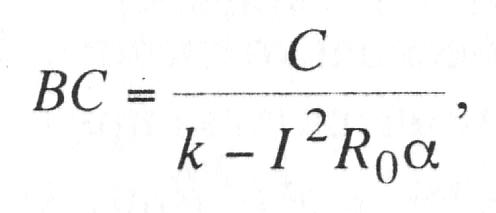(10.24)

т.е. длина по касательной ВС не зависит от момента времени t и остается постоянной за все время роста температуры. Ее называют постоянной времени нагревания и обозначают τ

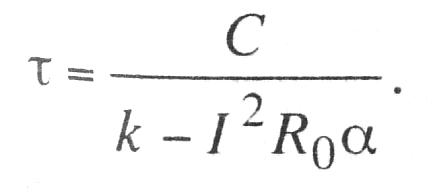(10.25)

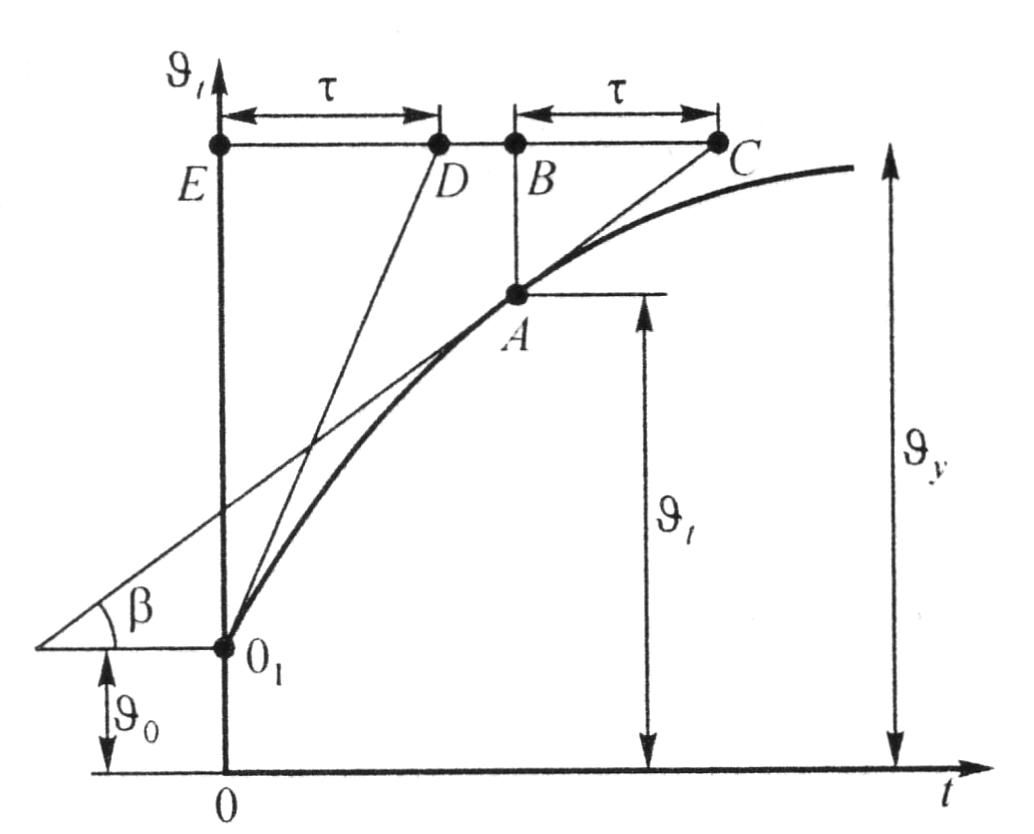
Рис. 10.4. Зависимость температуры от времени

Когда не учитывают влияние изменения температуры провода на его сопротивление и принимают α = 0, постоянная времени будет выглядеть следующим образом:

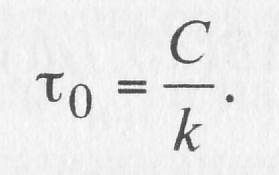(10.26)

Тогда выражение (10.15) с учетом уравнения (10.16) примет вид:

(10.27)

или

(10.28)

В выражении (10.27) значение , представлено двумя слагаемыми: первое слагаемое представляет собой температуру провода в момент времени t при начальной температуре, равной 0 (рис. 10.5, кривая 2). Второе слагаемое учитывает начальную температуру , а кривая 3 – падение этой слагаемой во времени. Сумма этих кривых и даст кривую 1 суммарной температуры . Подобно этому можно представить и процесс нагревания провода с учетом зависимости его сопротивления от температуры. Но здесь вопрос несколько сложнее. Первый член выражения (10.14) характеризует рост температуры при отсчете от начальной температуры, равной нулю. Пока k > I²R₀α, все протекает аналогично случаю, когда α = 0. Со вторым членом уравнения (10.14) дело обстоит иначе. Как и в выражении (10.15), он здесь характеризует постепенное понижение слагающей начальной температуры . В то же время про вод обтекается током I и, следовательно, его сопротивление превышает сопротивление R₀ не только за счет тока I, но и за счет слагающей от начальной температуры . Поэтому понижение за счет составляющей от менее интенсивно. На рис. 10.6 кривые 6, 4 и 3 повторяют кривые, приведенные на рис. 10.5, а кривые 5,2 и 1 заменяют их соответственно при R_t> R₀. Первый и второй члены выражения (10.14) относятся к случаю, когда по проводу протекает ток I и α >0. Рассмотрим, что получится, если ток будет отключен и охлаждение начнется с температуры . Подставим в выражение(10.14) I= 0:

(10.29)

Ток здесь не протекает и значение сопротивления не влияет ни на что. Если ток нагрузки в момент времени t₀ резко уменьшился бы до нуля (рис. 10.7, а), то процесс охлаждения (кривая АВ на рис. 10.7, 6) будет описываться выражением (10.29), где вместо следует принять .

Если ток нагрузки изменяется от I₁ до I₂ (рис. 10.8, а), то при нагревании (кривая АВ, рис. 10.8, 6) в выражении (10.14) ток I = I₁ и устанавливается значение в начале второго режима. Процесс охлаждения будет описываться также выражением (10.14) (кривая ВС, рис. 10.8, б), но здесь ток будет равен I₂.

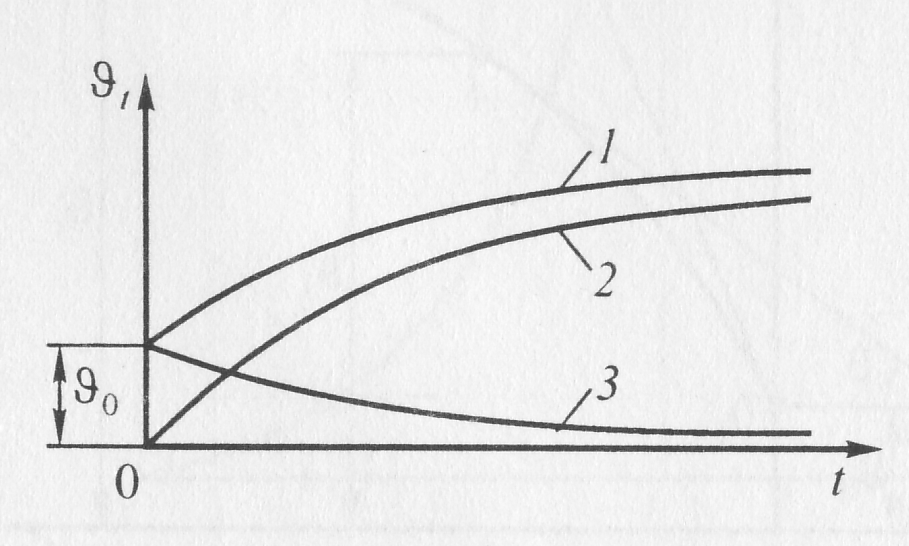
Рис. 10.5. Кривые определения значений членов выражения для нагревания проводов

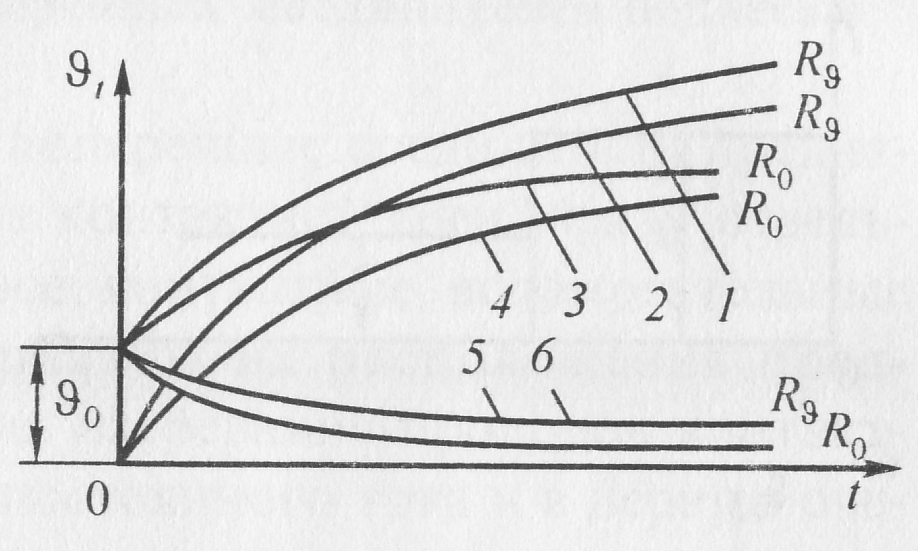
Рис. 10.6. Кривые определения значений членов формулы для нагревания провода при различных сопротивлениях

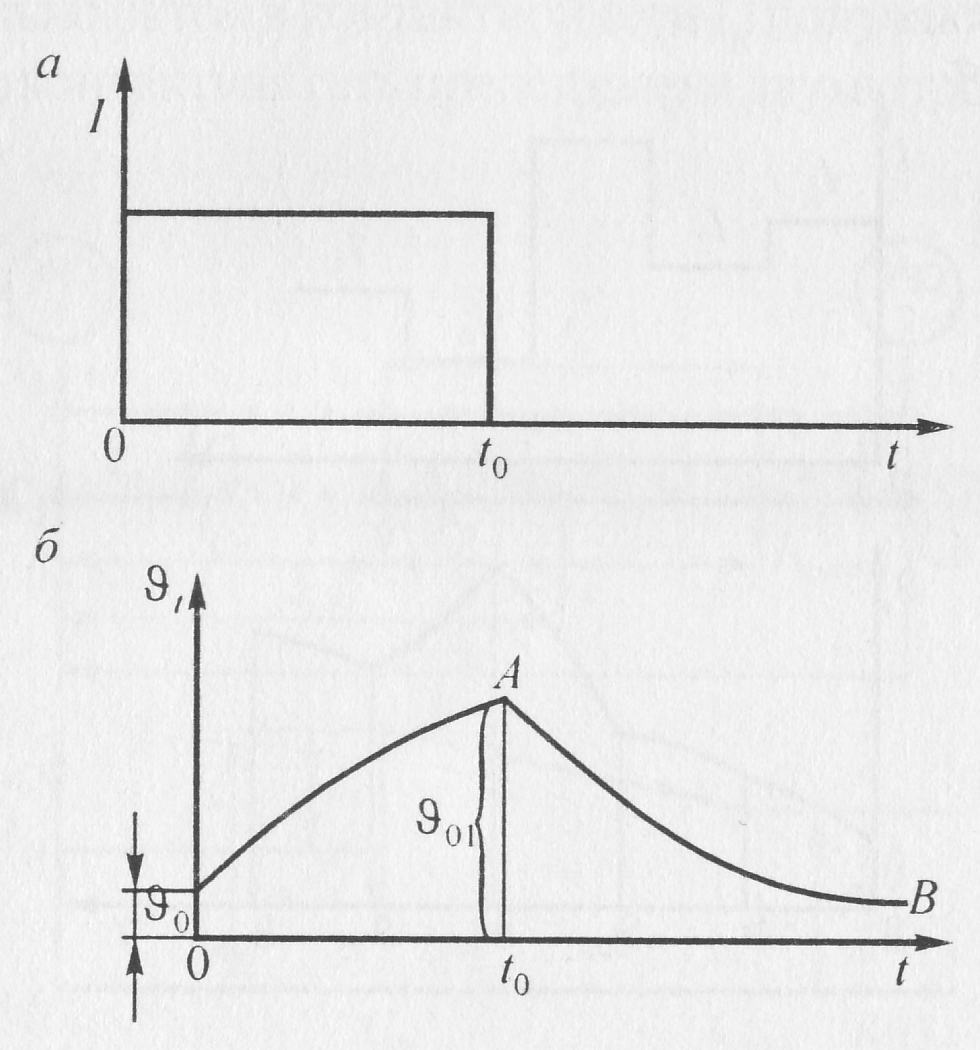
Рис. 10.7. Зависимость тока от времени (а) и кривая охлаждения провода при отключении тока (б)

Таким образом, если изменение тока в проводе представить ступенчатой линией (рис. 10.9), то на каждом участке кривая температуры будет строиться по выражению (10.14) и через оба члена будет проходить один и тот же ток I_i, соответствующий участку кривой тока. Здесь же будет определена начальная температура i-го участка кривой тока. Температура будет зависеть от тока I_i-1 на i-1-м участке. Кривая температуры на i-м участке будет зависеть от этой температуры и от тока на этом участке.

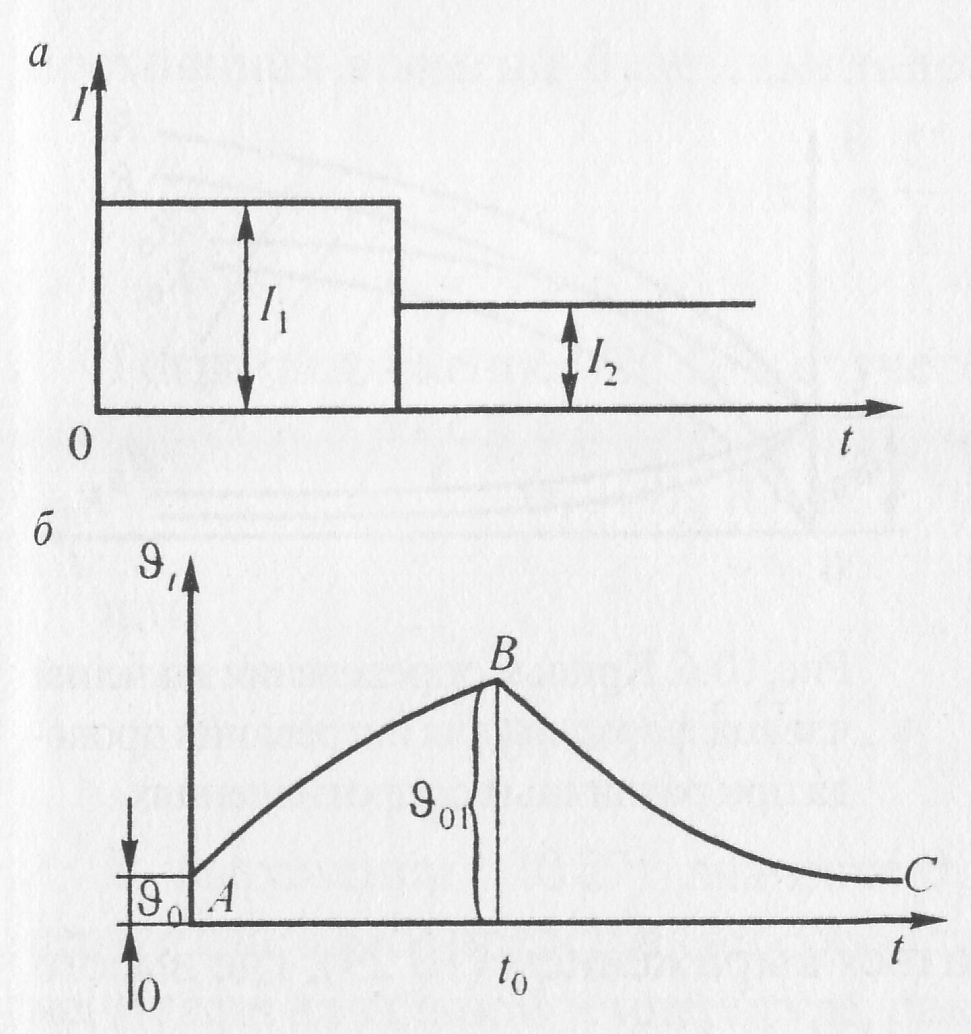
Рис. 10.8. Зависимость тока от времени (а) и кривая нагревания провода при уменьшении тока (б)

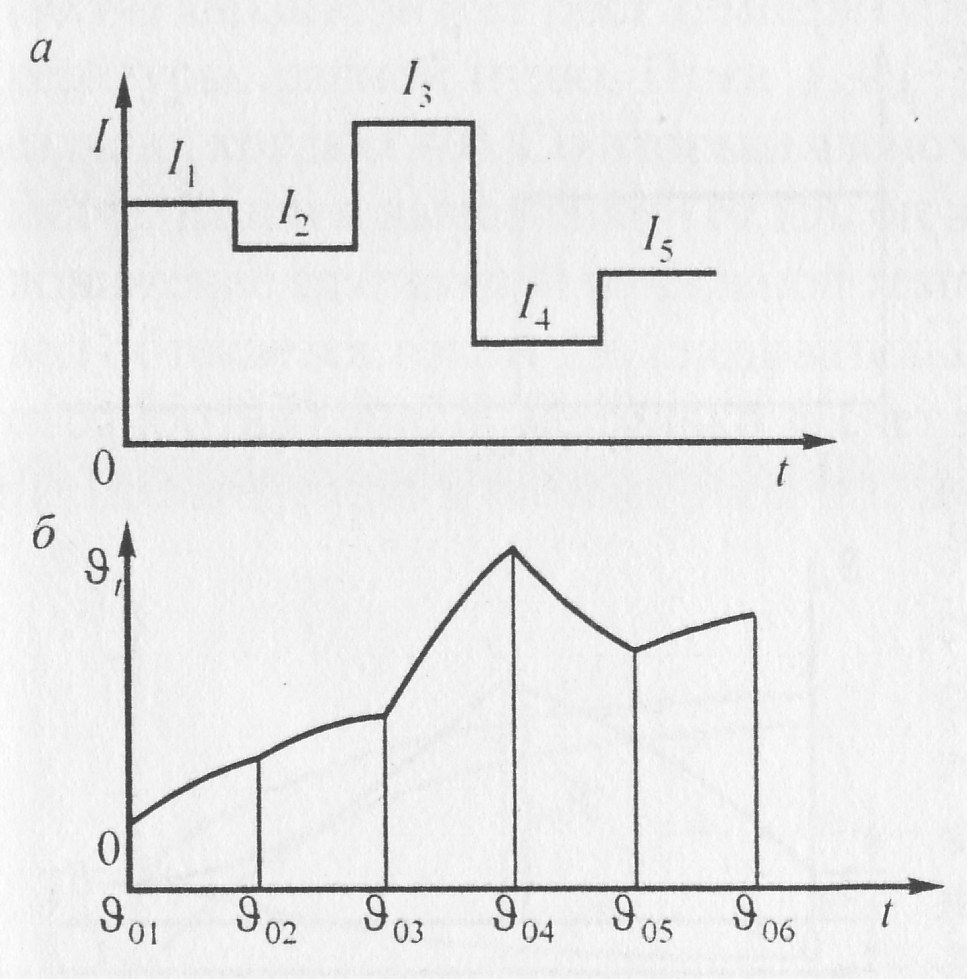
Рис. 10.9. Зависимость тока от времени (а) и кривая нагревания провода при изменяющемся токе (б)

Ранее были рассмотрены процессы нагревания проводов током, изменяющимся ступенчато. В действительности же ток в проводе контактной сети непрерывно изменяется. Поэтому при расчетах по выведенным формулам под током следует понимать некоторое постоянное значение, эквивалентное по своему воздействию на старение провода.

Однако отсутствие математических зависимостей механических характеристик от температуры и времени ее действия не позволяет определить токи эквивалентного значения. Поэтому приходится мириться с более грубыми допущениями. Далее под значениями токов будем понимать их эквивалентное значение по количеству выделяемого тепла (не по старению), т.е. так называемое «эффективное» значение (среднее квадратичное), взятое за время, соответствующее поставленной задаче. Если нагрузочные токи поездов в фидерной зоне не претерпевают резких и частых изменении, то под эквивалентным значением можно понимать их среднее значение за время хода по данной зоне.