Характеристики грунтов

Грунт	m0 кН/м3	с м	кПа
Пески крупные и средней крупности, глины, суглинки супеси твердые	140	0,35	400
Пески мелкие, глины, суглинки и супеси тугопластичные	105	0,30	300
Пески пылеватые, глины и супеси мягко-пластичные	80	0,25	200
Песчаные и глинистые почвы с примесью растительных остатков; заторфованные почвы, слежавшиеся в основании земляного полотна	50	0,20	100

Рассмотрим эпюры напряжений в грунте у подошвы фундамен­та в предельном состоянии. Опрокидывающий момент M, вызы­вающий напряжения у подошвы фундамента, может быть создан как горизонтальной силой P, так и вертикальной силой N_p при ее эксцентричном положении относительно оси фундамента. В за­висимости от опрокидывающего момента эпюра напряжений у подошвы фундамента, уравновешивающая силу N (где N — рав­нодействующая сил реакции грунта) будет принимать тот или иной вид. Так, при наличии одной силы N_p приложенной в цент­ре фундамента, напряжение грунта и ему соответству­ет деформация ₀. Эпюры напряжений и деформации будут иметь вид прямоугольника (рис. 4.25, а). При появлении опрокидываю­щего момента М, вызванного эксцентричным приложением силы N_p или введением новой силы Р, фундамент получит некоторый на­клон. Эпюры напряжений и деформаций получат вид, приведенный

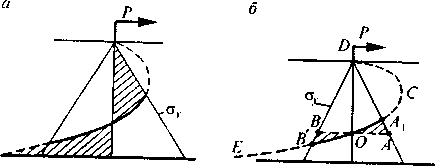
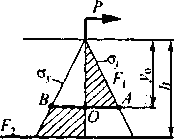
Рис. 4.24. Расчетная схема для выбора расчетной эпюры по передней и задней стенкам фундамента в предельном состоянии

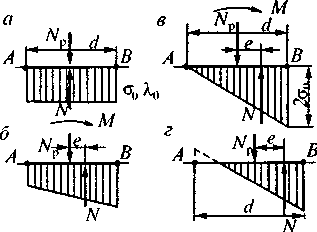
Рис. 4.25. Эпюры давлений у по­дошвы фундамента в пределах уп­ругого сжатия грунта

Эпюры напряжений и деформаций получат вид, приведенный на рис. 4.25, б где силы N_p и N создают пару, уравновешиваю­щую опрокидывающий момент М. Когда увеличивается момент М, возрастает наклон фунда­мента и, следовательно, должен увеличиться момент пары сил. Сила N_p (сумма всех вертикаль­ных сил, действующих на соору­жение, включая силу тяжести фундамента) может быть по­стоянной только при увеличе­нии плеча пары N и N_p , т.е. по­степенного удаления силы N от силы N_p и приближения ее к краю фундамента.

При дальнейшем увеличении опрокидывающего момента эпюра примет вид, представленный на рис. 4.25, г. Так как грунт не может работать на растяжение, то у точки А подошва отрывается от него и происходит так называемое «раскрытие шва». Реактивный момент бу­дет тем большим, чем на большей длине это произойдет. Площадь эпю­ры давлений все время остается постоянной, равной сумме вертикальных сил, а поэтому е увеличивается при возрастании напряжения под реб­ром Я При достижении определенного предела сжатия грунта оно уже не будет упругим и нарастание напряжения под ребром В (рис. 4.26, а) будет происходить медленнее, чем увеличение угла поворота (до этого предела указанные величины находятся в линейной зависимости). Точ­кой D отмечено значение, какого бы достигло напряжение, если бы грунт при всех значениях а отвечал закону упругости. Если после некоторого напряжения _п сопротивление грунта почти не увеличивается, то, оче­видно, эпюра получит вид, представленный на рис. 4.26, б. Без ощути­мой погрешности можно для определения предельного момента (в запас прочности) принять взамен эпюры на рис. 4.26, а фиктивную эпюру давлений, показанную на рис. 4.26, в, так как изменение эксцентриситета, очевидно, будет nнезначительным.

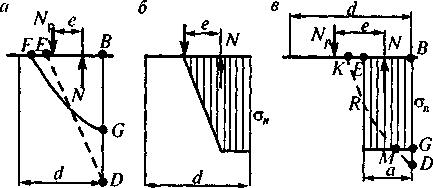
Рис. 4.26. Эпюры давлений у подошвы фундамента за пределами упругого сжатия грунта

Некоторое уменьшение эксцентриситета из-за потери площади МGD компенсируется увеличением его от потери площади КЕК. Эту эпюру, очевидно, и можно принять для расчета.

При использовании методов расчета, основанных на распре­делении усилий в грунте при эксплуатации, наибольшую труд­ность представляет разделение усилий между подошвой и стенка­ми фундамента. Обычно сначала определяют допустимый момент, действующий на подошву фундамента, а затем, взяв остаток меж­ду расчетным моментом и моментом, воспринимаемым подошвой, проверяют напряжение у боковых стенок; полагая тем самым, что деформации грунта у подошвы не связаны с деформациями грун­та у боковых стенок, что, конечно, неверно. Также неверным яв­ляется расчет, основанный на каком-либо другом распределении эпюр в состоянии устойчивости. Пока не имеется данных, кото­рые могли бы связать деформации грунта у подошвы и боковых стенок между собой.

Наиболее удобным, видимо, будет расчет без учета распреде­ления опрокидывающего момента между подошвой и боковыми стенками. Этого можно достигнуть, определяя наибольший оп­рокидывающий момент (предельный) как сумму наибольших мо­ментов для боковых стенок и подошвы. Такой подход будет верным, так как опора вывернется только после того, как момент внешних сил превысит этот суммарный наибольший момент сил реакций боковых стенок и подошвы.

При определении предельного опрокидывающего момента проверку на деформации (наклон фундамента) можно не проводить, так как характеристики грунта в нормативах заданы, исхо­дя из условий допустимости соответствующих перемещении фун­даментов опор при эксплуатации.

Предельный опрокидывающий момент для призматического фундамента. Расчетная эпюра активных и реактивных сил, дей­ствующих на фундамент в предельном состоянии, представлена на рис. 4.27. В предельном состоянии на фундамент действуют горизонтальная Р₀ и вертикальная (сила тяжести) N₀ силы.

Если на опору в одной вертикальной плоскости действует не­сколько горизонтальных сил Р₁ , Р₂,…, Р_п с плечами H₁,H₂,..,H_n и моментов M₁ , M₂, ..., M_n, то для расчета удобно найти суммарный момент относительно поверхности земли:

M₀= (4.29)

Частное от деления M₀ на равно эквивалентному плечу этой силы Н=М₀/Р₀.

Для определения суммар­ного реактивного момента составим два уравнения рав­новесия. Первое из них мо­жет быть представлено в виде

(4.30)

где R₁ и R₂— равнодей­ствующие сил реакций грун­та на боковые стенки.

Второе условие равно­весия—сумма моментов от­носительно точки О:

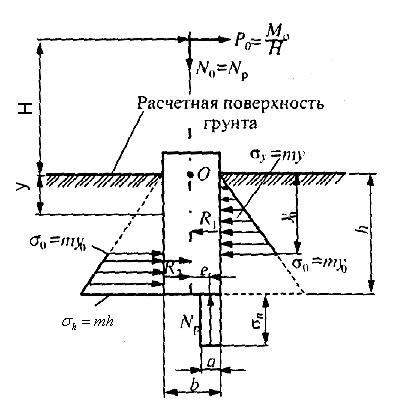
Рис. 4.27. Расчетная схема нагрузки при­зматического фундамента в предельном состоянии

В этих уравнениях

;

(4.31)

Соответственно

;

(4.32)

где my₀ и mh — предельные давления на боковые стенки соответственно на глубине y₀ и h.

Значения величин из выражений (4.31) подставим в уравнение (4.30)

(4.33)

Подставляя выражения (4.31) в (4.32) и полученный результат в (4.7.9), получим

(4.34)

Из уравнения (4.33) можно определить

(4.35)

Исследования показывают, что значение у₀ для опор контакт­ной сети изменяется в очень небольших пределах, оставаясь всегда близким к . Это соответствует случаю, когда на опору дей­ствует только опрокидывающий момент, а горизонтальная и вер­тикальные силы равны нулю. Другими словами, второй член подкоренного выражения (4.35) всегда значительно меньше первого. Такое соотношение позволяет упростить выражение (4.35). Выне­сем h²/2 за знак радикала и используем известное положение тео­рии приближенных вычислений ( при a«1), тогда

(4.36)

Найдем значение у_о^з После возведения в степень множителя в скобках отбросим два члена уравнения из-за их малого значе­ния. Тогда

(4.37)

Величину y₀³ из выражения (4.37) подставим в формулу (4.34) и после преобразований получим

(4.38)

Решим уравнение (4.38) относительно М₀:

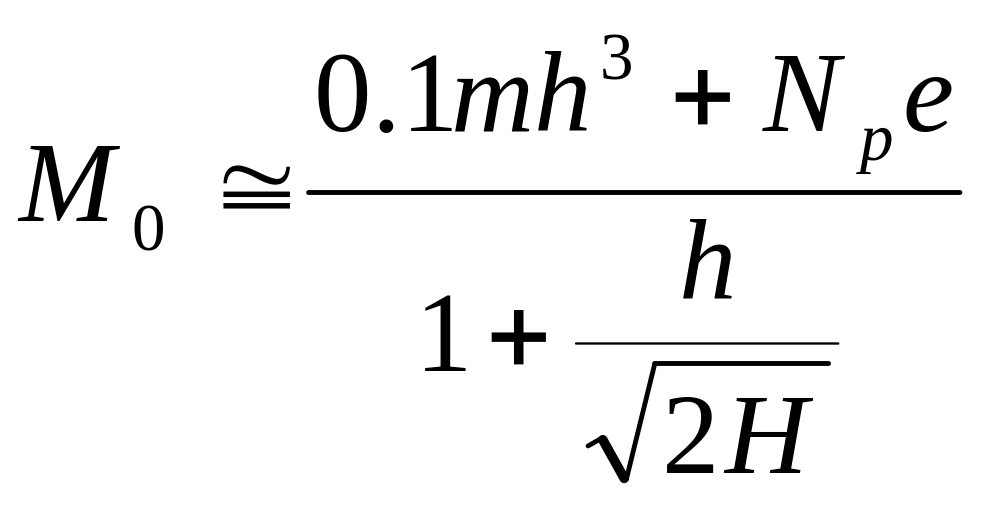(4.39)

Если на опору момент, то и фундамент действует только опрокидывающий момент, то

и

Предположим, что в формуле (4.39) Н = , тогда

(4.40)

В выражениях (4.39) и (4.40) не известно значение е. Оно может

быть найдено из условия, что е = (см. рис. 4.27). Так как а = N_p/ , то

е=d/2-N_p / (4.41)

где к = 0,7 — коэффициент однородности; _п — предельное давле­ние грунта на подошву фундамента (см. таблицу); b и d — ширина и толщина фундамента. Значение е примерно равно 0,4 d.

Определение допустимой нагрузки для фундамента. Приведен­ные выше выводы и расчетные формулы для определения предель­ной горизонтальной силы и предельного момента даны для неко­торых обезличенных условий. Согласно принятой терминологии условным назван фундамент призматической формы прямо­угольного поперечного сечения (без лежней или с лежнями), зако­панный на горизонтальной площадке при отсутствии в непосред­ственной близости железнодорожного пути и при нагрузке, в ко­торой доля постоянной составляет 35 %. Всякий фундамент, усло­вия работы которого будут отличаться от приведенных, называют заданным. Предельную нагрузку для заданного фундамента опре­деляют, умножая предельную нагрузку условного фундамента на коэффициенты условий работы, значения которых установлены опытным путем. В соответствии с этим предельную нагрузку для призматического фундамента другой формы и в других условиях работы определяют по выражению

М=М₀m_ф m_от m_вб m_у m_п m_нг (4.42)

где m — коэффициенты, учитывающие: m_ф — форму поперечного сечения; m_ОТ — очертание поверхности грунта в месте расположе­ния фундамента; m_вб — вибрации (колебания) грунта около фундамента от проходящих поездов; т_у — повышенное уплотне­ние грунта при забивке фундамента; m_нг — долю постоянной на­грузки в суммарной.

Коэффициент m_ф для фундамента без лежней прямоугольного сечения рекомендуется принимать равным единице, круглого — 0,9 и двутаврового —1,1 (при действии усилия вдоль его стенки, т.е.перпендикулярно полке). Коэффициент m_от при нагрузке, действу­ющей в плоскости, перпендикулярной бровке земляного полотна, определяют по рис. 4.28 в зависимости от очертания поверхности грунта в месте установки фундамента и направления горизонталь­ной нагрузки. Если нагрузка действует в плоскости, параллельной бровке земляного полотна, m_от принимают равным единице.

При вибрации (колебании) грунта около фундамента от прохо­дящих поездов, т.е. для опор, устанавливаемых в теле земляного полотна главных путей, коэффициент m_вб = 0,9, а при отсутствии колебаний m_вб = 1. Коэффициент т_y принимают равным единице для закапываемых фундаментов, т. е. устанавливаемых в котлова­не, вырытых вручную или буровой машиной; 1,2 — для свайных фундаментов сплошных сечений и пустотелых, забитых с закры­тым концом; 1,1 — для свайных пустотелых фундаментов, забитых с открытым концом, двутавровых и трехлучевых. Коэффициент m_п=1 при расположении фундамента за кюветом или при расстоя­нии от оси пути до ближайшей грани фундамента более 4 м, или при моменте, действующем в плоскости, параллельной оси пути m_п=1,2 — при моменте, действующем в сторону пути при расстоянии от оси ближайшего пути до передней грани фундамента менее 3,2 м (при расстоянии от 3,2 до 4 м m_п=1,1) и m_п=1,1 при моменте, действующем в сторону поля, и расстоянии от оси бли­жайшего пути до ближайшей грани фундамента до 4 м.

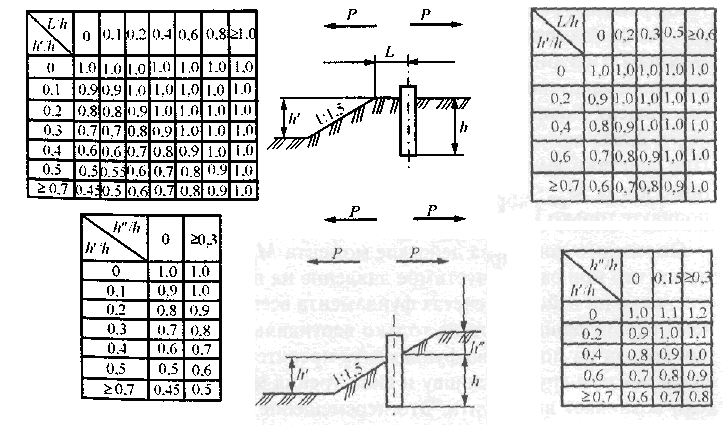
Рис. 4.28. Таблицы и схемы для определения коэффициента '»_от, учитывающего влияние очертания поверхности грунта

Перемещение фундамента связано со временем действия силы, поэтому временные нагрузки оказывают меньшее влияние, чем постоянные, поэтому коэффициент т_нг определяется по формуле

m_нг = 1/(0,5+1,43 ), (4.43)

где — коэффициент, характеризующий долю постоянной нагруз­ки в суммарной.

Если = 0,35, то m_нг = 1 (для условного фундамента все коэф­фициенты равны 1,0, а = 0,35). При расчетных моментах М_рп (от постоянной нагрузки) и М_рп (от временной нагрузки), дейст­вующих в одном направлении,

= М_рп/(М_рп+М_рв) (4.44)

Выражение (4.44) верно при Н»h, т.е. практически всегда при расчете фундаментов опор контактной сети, так как высота опоры Н всегда > глубины заделки грунта h. Если действует только по­стоянная нагрузка ( = 1), то т_нг=0,5 (почти двойной коэффици­ент запаса). Если действует только временная нагрузка ( = 0), то м_нг=2, т.е. допускается вдвое большая нагрузка, чем предельная. При действии моментов М_рп и М_рв в противоположных направлениях, когда М_рп<М_рв, м_нг= 2,0. Если М_рп > М_рв, то расчет выполняют только на действие момента М_рп при m_нг = 0,52.

Определим допустимое давление на подошву фундамента, учи-! тывая, что при расчетах фундамента всегда необходимо проверять его также на действие только вертикальной нагрузки. Вертикаль­ному перемещению фундамента препятствуют возникающие реак­ции грунта на подошву и сила трения между боковыми стенками фундамента и грунта. Это перемещение несколько увеличивается, если возникает вибрация грунта от проходящих поездов. В соот­ветствии с этим допустимая вертикальная нагрузка

(4.45)

где и — периметр попе­речного сечения фунда­мента (для фундамен­тов таврового, двутав­рового сечения пери­метр определяют по контурам, показанным на рис. 4.29); h — глуби­на фундамента; — пре­дельное удельное сопро­тивление трения грунта по вертикальной поверхности фундамента (для закопанных фундаментов независимо от категории грунта ре­комендуется принимать 9,81 кПа); _п — предельное давление грунта на подошву фундамента (см. таблицу); F_п — площадь подошвы за­капываемого фундамента или плиты, на которую он опирается.

Свайные фундаменты, как правило, на вертикальную нагрузку не проверяют.

Для закрепления поддерживающих и опорных конструкций в грунте разработаны типовые способы и конструкции подземной части, включая и непосредственную заделку железобетонных опор. При выборе стремятся использовать типовые решения. Способ зак­репления опор в грунте выбирают по нормативному изгибающему моменту опоры. При этом учитывают все условия, определяемые местом установки опоры: габарит относительно оси пути, направ­ление действия опрокидывающего момента, характеристики грун­та, поперечный профиль (площадка, насыпь или выемка).

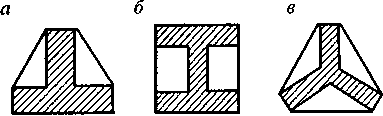
Рис. 4.29. Расчетная схема для определения расчетного периметра таврового (а), двутав­рового (б) и трехлучевого (в) сечений