- •Section 2. Aerodynamics of bodys of revolution Theme 12. The aerodynamic characteristics of Bodys of revolution, fuselages and their analysis
- •12.1. Lifting force of a body of revolution.
- •12.1.1. Lift of a nose part.
- •12.1.2. Lift of the cylindrical part.
- •12.1.3. Lift of the rear part.
- •12.2. Aerodynamic moment of a body of revolution. Coordinate of aerodynamic center.
- •12.2.1. Aerodynamic moment of a nose and coordinate of an aerodynamic center.
- •12.2.2. Coordinate of the aerodynamic center of the cylindrical part.
- •12.2.3. Coordinate of the aerodynamic center of the rear part.
- •12.2.4. Coordinate of the aerodynamic center of body of revolution in a whole.
12.2. Aerodynamic moment of a body of revolution. Coordinate of aerodynamic center.
According to the theory of a thin (elongated) body the longitudinal moment is determined under the formula
![]() (12.14)
(12.14)
As the lifting (normal) force was determined for separate parts of a body of revolution (for nose, cylindrical and rear parts), and moment characteristics are expedient for calculating also for parts of body of revolution.
12.2.1. Aerodynamic moment of a nose and coordinate of an aerodynamic center.
Let's use
the results of the theory of an elongated body, according to which
the factor of pressure on surface of the body of revolution at
streamlining under the angle of attack is determined by the formula
(12.1)
![]() .
.
We have
 ,
,
 .
(12.15)
.
(12.15)
Let's
consider an integral function
 :
:
 2
2
Having accounted it an aerodynamic moment of the nose part
![]() ,
(12.16)
,
(12.16)
where
![]() - relative volume of the nose part.
- relative volume of the nose part.
Coordinate
of the nose aerodynamic center relatively to nose of the
body
of revolution in shares of length of the nose part
![]() :
:
- at
absence of the air intake in the nose part
![]() .
.
- at
presence of the air intake in the nose part
![]() .
.
Obtained formulae can be used at any Mach numbers (despite of the fact that the theory of an elongated body was applied which is fair for calculation of the derivative only at subsonic speeds ).
|
For conical nose part
|
|
For chambered nose part
|
It is necessary to mark, that for bodies with the parabolic nose part coordinate of the aerodynamic center practically does not vary with increase of Mach numbers .
12.2.2. Coordinate of the aerodynamic center of the cylindrical part.
In the
subsonic flow (![]() )
lift of the cylindrical part
)
lift of the cylindrical part
![]() ,
therefore the moment characteristics of the cylindrical part are not
calculated.
,
therefore the moment characteristics of the cylindrical part are not
calculated.
In the
supersonic flow (
)
coordinate of the aerodynamic center
![]() ,
as well as the derivative
,
depends on Mach number, aspect ratio of the nose and type of coupling
of nose and cylindrical parts (Fig. 12.7):
,
as well as the derivative
,
depends on Mach number, aspect ratio of the nose and type of coupling
of nose and cylindrical parts (Fig. 12.7):
![]() .
.
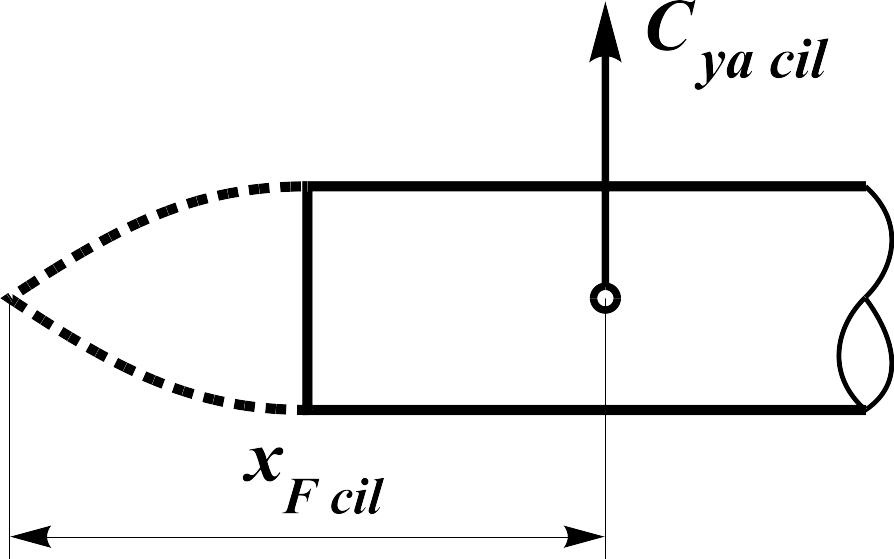 Let's
express a coordinate of the aerodynamic center of the cylindrical
part
Let's
express a coordinate of the aerodynamic center of the cylindrical
part
![]() in shares of fuselage nose length
in shares of fuselage nose length
 ,
,
![]() ,
(12.17)
,
(12.17)
where the factor value can be accepted as the following ones:
- for conical nose part ;
- for a nose with chambered generative line and tangent coupling .
Fig.
12.7. Coordinate of the aero-dynamic center of the cylindrical part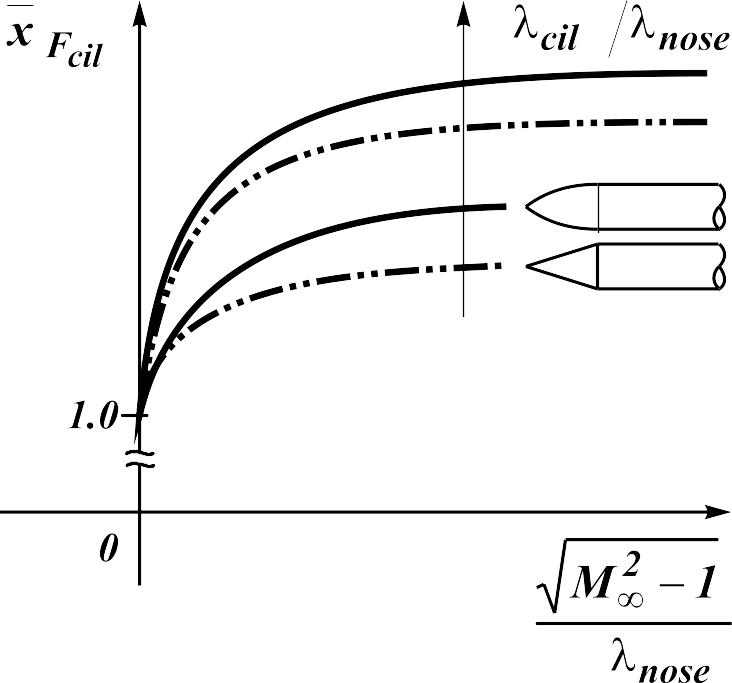
![]() a coordinate of the aerodynamic center depends only on the attitude
of aspect ratios of cylindrical and nose parts of the body of
revolution
a coordinate of the aerodynamic center depends only on the attitude
of aspect ratios of cylindrical and nose parts of the body of
revolution
![]() .
.
At presence
of smooth coupling of the nose and cylindrical parts the aerodynamic
center
![]() locates a little bit distant, than in case of conical nose and
intersecting coupling.
locates a little bit distant, than in case of conical nose and
intersecting coupling.
12.2.3. Coordinate of the aerodynamic center of the rear part.
Irrespectively of the shape of the rear part, for any Mach numbers coordinate of the aerodynamic center of rear part can be calculated by the formula

![]() (12.18)
(12.18)
i.e. we accept, that rear part aerodynamic center locates in its middle.
12.2.4. Coordinate of the aerodynamic center of body of revolution in a whole.
Let's
consider the configuration of a body of revolution (Fig. 12.8). In
this case coordinate of the aerodynamic center relatively to nose is
determined as
![]() :
:
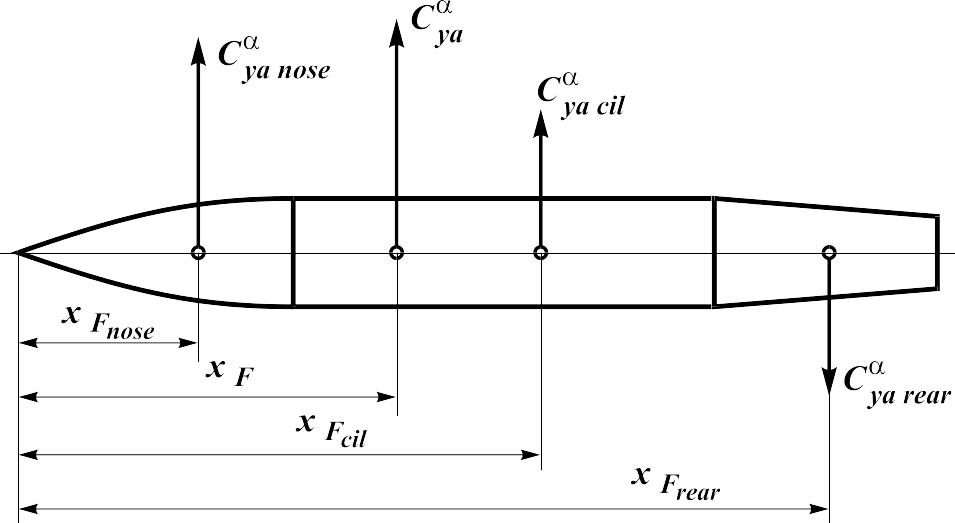
Fig. 12.8.
 ,
(12.19)
,
(12.19)
where .
It is
necessary to mark, that at subsonic speeds (
)
and small angles of attack, at which
the aerodynamic center of the body of revolution can place ahead of a
nose, i.e.
![]() .
.
1![]() Is
used.
Is
used.
2 Is used
Is used