11.4. Операції зі складною обліковою ставкою
Коли в практиці облікових операцій використовують складну облікову ставку, то процес дисконтування здійснюється з уповільненням, адже на кожному кроці в часі облікова ставка застосовується не до початкової суми, а до суми, зменшеної на величину дисконту, визначеного на попередньому кроці. Дисконтування за складною обліковою ставкою здійснюється за формулою:
P = S (1 – dc)n,
де dc — складна облікова ставка; S — сума майбутніх платежів, на яку нараховується відсоткова ставка; (1 – dc)n — множник дисконтування.
Дисконт у такому разі:
Dd = S – S (1 – dc)n = S (1 – (1 – dc)n).
Приклад 7. Якою буде сума дисконту при продажу фінансового інструменту на суму 5000 грн., якщо строк його погашення становить 5 років, а покупець використав складну річну облікову ставку, яка дорівнює 8 %?
Розв’язання: P = S (1 – d)n = 5000 (1 – 0,08)5 = 4059 грн.
Дисконтування за складною обліковою ставкою зумовлює вигідніший для боржника результат, ніж при дисконтуванні за простою обліковою ставкою, оскільки боржник отримає більшу велику суму Р.
Дисконтування m разів на рік
У такому разі використовують номінальну облікову ставку f. У кожному періоді дисконтування здійснюється за ставкою f/m:
P = S (1 – f/m)mn,
де mn — загальна кількість періодів дисконтування.
Дисконтування не один, а m разів на рік уповільнює цей процес і зменшує суму дисконту за всіх інших рівних умов. Дисконтування за складною обліковою ставкою призводить до результату, який вигідніший для боржника, ніж при дисконтуванні за простою обліковою ставкою.
Під ефективною обліковою ставкою розуміють складну річну облікову ставку, еквівалентну номінальній при заданому значенні числа дисконтування на рік:
Ефективна облікова ставка менша за номінальну.
Нарощення за складною обліковою ставкою:
;
11.5. Порівняння інтенсивності процесів нарощення і дисконтування за різними відсотковими ставками
Для розрахунку нарощеної суми і дисконтування використовувались різні види відсоткових ставок: in, i, j, d, dc, f. За однакових умов угоди їх використання призведе до різних результатів. Треба порівняти результати нарощення і дисконтування за різними видами відсоткових ставок. Для розв’язання цього завдання достатньо порівняти множники нарощення і дисконтні множники.
Результати порівняння залежать від числа періодів нарахування відсотків:
для множників наростання —
n < 1 (1 + i)n < (1 + in) < (1 – nd)–1< (1 – d)–n;
n > 1 (1 + ni) < (1 + i)n < (1 – d)–n < (1 – nd)–1;
n = 1 (1 + in) = (1 + i)n < (1 – d)–n = (1 – nd)–1;
для дисконтних множників —
n < 1 (1 – d)n < (1 – nd) < (1 + in)–1 < (1 + i)–n;
n > 1 (1 – nd) < (1 – d)n < (1 + i)–n < (1 + in)–1;
n = 1 (1 – nd) = (1 – d)n < (1 + i)–n = (1 + in)–1.
11.6. Визначення строку платежу і рівня відсоткових ставок
У ряді випадків, головним чином при розробці умов фінансових операцій, зустрічаються з необхідністю розв’язання зворотних задач — визначення довготривалості позичок, числа періодів нарощення, ставки відсотків або облікової ставки.
Знаходження відсоткових ставок
1. Для простої відсоткової ставки:
2. При нарощенні за складною річною ставкою:
3. При нарощенні за номінальною ставкою відсотків m разів на рік:
4. При дисконтуванні за простою обліковою ставкою:
5. При дисконтуванні за складною обліковою ставкою:
6. При дисконтуванні за номінальною обліковою ставкою m разів на рік:
Визначення строку позички
1. За простою ставкою відсотків:
2. За складною ставкою відсотків:
3. При нарощенні за номінальною ставкою відсотків j/m разів на рік:
4. При дисконтуванні за простою обліковою ставкою:
5. При дисконтуванні за складною обліковою ставкою:
6. При дисконтуванні за номінальною обліковою ставкою m разів на рік:
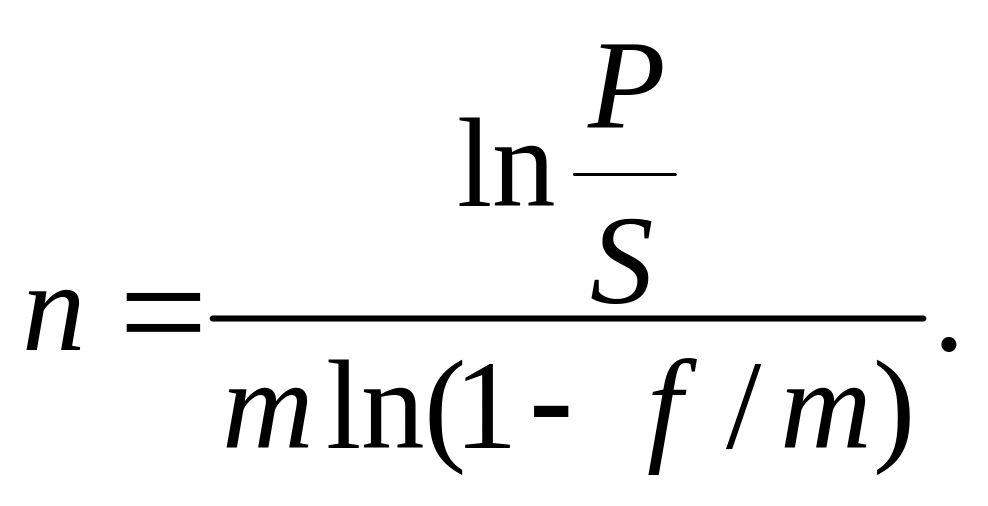
Приклад 8. В умовах випуску сертифікатів (номіналом 1000 грн.) були передбачені викупні суми, які залежать від строку зберігання: при п’ятирічному терміні виплачувалось 1415 грн., десятирічному — 2595 грн. Які значення річних складних ставок відсотків, котрі дають таке нарощення?
Розв’язання: i = (S/P)1/n – 1 = (1415/1000)1/5 – 1 = 0,07189;
i = (2595/1000)1/10 – 1 = 0,1.
Приклад 9. Вексель виписаний на строк 2 роки. Якою повинна бути складна облікова ставка, щоб при обміні векселя власник отримав 90 % його суми?
Розв’язання:
P/S = 0,9 n = 2 dc = 1
– (P/S)1/n = 1 –
=
0,0513.
Приклад 10. Кредит надано у сумі 1000 грн. за ставкою складних відсотків 10 % річних. Боржник повинен у кінці строку позички повернути 1200 грн. Необхідно визначити, на який строк було надано кредит.
Розв’язання:
року.