1. Вспомогательный материал: сигналы, спектры, передаточные функции

1.1. Понятие спектра сигнала

В технике связи используются сигналы различной формы: прямоугольные, треугольные, косинус-квадратные

— они показаны на рис. 1.1 (кривые 1, 2 и 3 соответственно), а также некоторые другие.

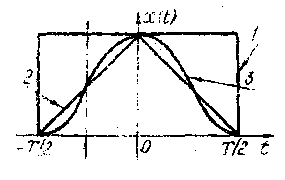
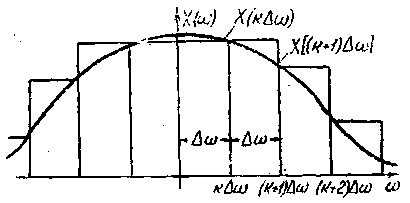
Рис. 1.1 Рис. 1.2

Каждому сигналу сопоставляют спектр с помощью преоб­разования Фурье (точнее, прямого преобразования Фурье)

. (1.1)

Для сигналов произвольной (в том числе и бесконечной) длительности последнюю формулу пишут в более общем виде:

. (1.2)

Интегралы (1.1) и (1.2) для всех частот оп­ределяют комплексную функцию - спектр, физический смысл которого становится ясным из доказанной в курсе математического анализа [3, 4] формулы обратного преобра­зования Фурье

, . (1.3)

Действительно, в соотношении (1.3) можно приближенно - в соответствии с методом прямоугольников [3, 4], согласно которому интегрируемая функция приближается последова­тельностью прямоугольников (рис. 1.2), — подменить ин­теграл суммой и переписать это соотношение следующим образом:

. (1.4)

При записи результата (1.4) использовалось соотношение Эйлера

.

Соотношение (1.4) показывает, что произвольный сиг­нал представим в виде бесконечного набора (суммы) косинусоид и синусоид с частотами и, вообще говоря, комплексными коэффициентами. Если отвлечься от постоян­ного для всех значений номера множителя , то этими коэффициентами при функциях и служат отсчетные значения спектра . Итак, каждый сигнал «состоит» из косинусоид и синусоид (более точно, является их суммой) с соответствующим образом подобранными коэф­фициентами.

Иногда предпочтительно отказаться от эйлерова представ­ления комплексной экспоненциальной функции и огра­ничиться приведенным выше представлением сигнала :

, (1.4а)

которое переходит в равенство (1.3) при стремлении к нулю ; соотношение (1.4а), а вместе с ним и предельное равенство (1.3) можно интерпретировать следующим образом: каждый сигнал является суммой комплексных экспоненциаль­ных функций, чья вещественная часть — косинусоида, а мни­мая часть — синусоида, с коэффициентами , определяемыми формулой (1.2).

Определение 1.1. Совокупность всех коэффициен­тов , , точнее, их предельных значений при , т. е. функция , , называется спектром сигнала .

Экспоненциальные функции и , ,обладают замечательным свойством - ортогональностью на оси .

Определение 1.2. Две в общем случае комплексные функции и , , называются ортогональными на интервале , если выполняется равенство

, (1.5)

где чертой обозначен переход к комплексно-сопряженной ве­личине *.

Разумеется, для вещественных и равенство (1.5) переписывается без черты над :

. (1.5а)

Условию ортогональности (1.5а) удовлетворяют, в частности, косинусоиды и синусоиды различных частот при , :

, , .

Таким образом, представления сигналов с помощью об­ратного преобразования Фурье (1.3) (или приближенные их представления с помощью формулы (1.4а)) являются по су­ществу ортогональными разложениями. В дальнейшем (см. главу 2) нам встретятся ортогональные синтезаторы (корректоры) частотных характеристик, которые осуществля­ют синтез заданных зависимостей в виде суммы ортогональ­ных функций со специальным образом выбираемыми коэф­фициентами. Свойство ортогональности облегчает процесс отыскания этих коэффициентов (см. главу 4).

Вернемся к спектрам сигналов. Допустим, что комплекс­ная функция частоты - спектр сигнала - пред­ставима в виде

,

где, в соответствии с теорией комплексных чисел и функций [4], - модуль спектра, а - его аргумент с обратным знаком. При этом

, (1.7а)

, (1.7б)

где - реальная часть , - мнимая часть , так что

.

Геометрический смысл соотношений (1.6) ... (1.8) иллюстри­рует рис. 1.3.

Наделяя и физическим содержанием, иногда называют амплитудно-частотной характерис­тикой сигнала (АЧХ), а - его фазочастотной характеристикой (ФЧХ). Та­кая терминология представ­ляется уместной; действи­тельно, если рассмотреть произвольно выбранную частотную компоненту сигнала (1.3) (при ):

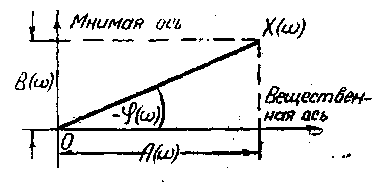
^{Рис. 1.3}

^,

то станет понятным, что определяет ее амплитуду, а - начальную фазу (с обратным знаком).

Пример. Исследуем спектр прямоугольного импульса (см. рис. 1.1). В соответствии с формулой (1.1) находим

. (1.9)

Построим график полученного спектра (рис. 1.4). Обра­тим внимание на то, что данный спектр является вещественной функцией частоты (этим свойством

обладают спектры всех четных сигналов). Рассматривая рис. 1.4, можно за­метить, что максимальное значение функция (1.9) принимает в точке (оно равно, как легко проверить, раскрыв не­определенность по правилу Лопиталя [3, 4], Т); другими сло­вами, наибольший «вклад» при «построении» прямоуголь­ного импульса вносит функция нулевой частоты - так называемая постоянная составляющая, наименьший (нуле­вой) «вклад» вносят комплексные экспоненты с частотами , , , ..., коэффициенты при них

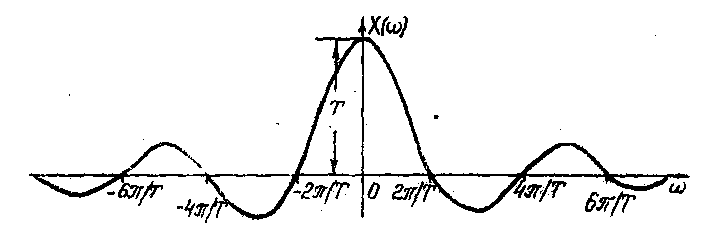
Рис. 1.4

равны нулю. Влияние на форму прямоугольного сигнала экспоненциальных функций при становится все меньше. Действительно, спектр этого сигнала стремится к нулю с ростом частоты: .