Л исты 3, 4 Пересечение поверхностей плоскостями
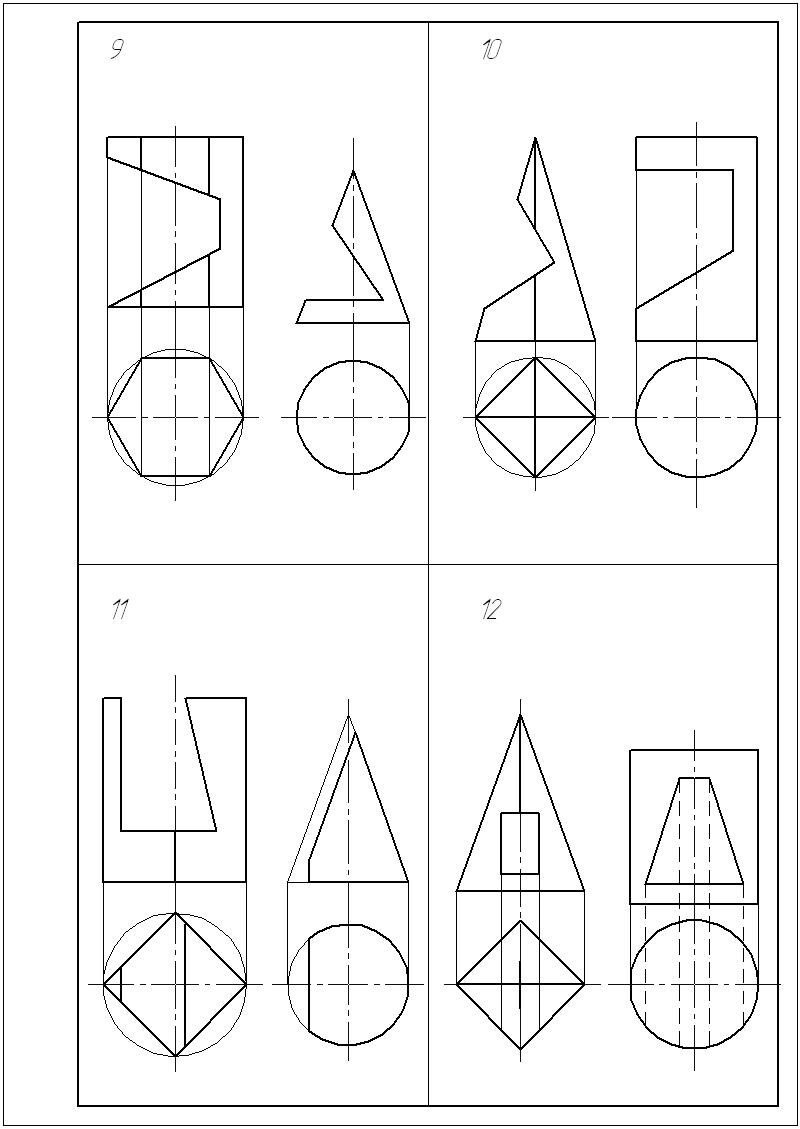
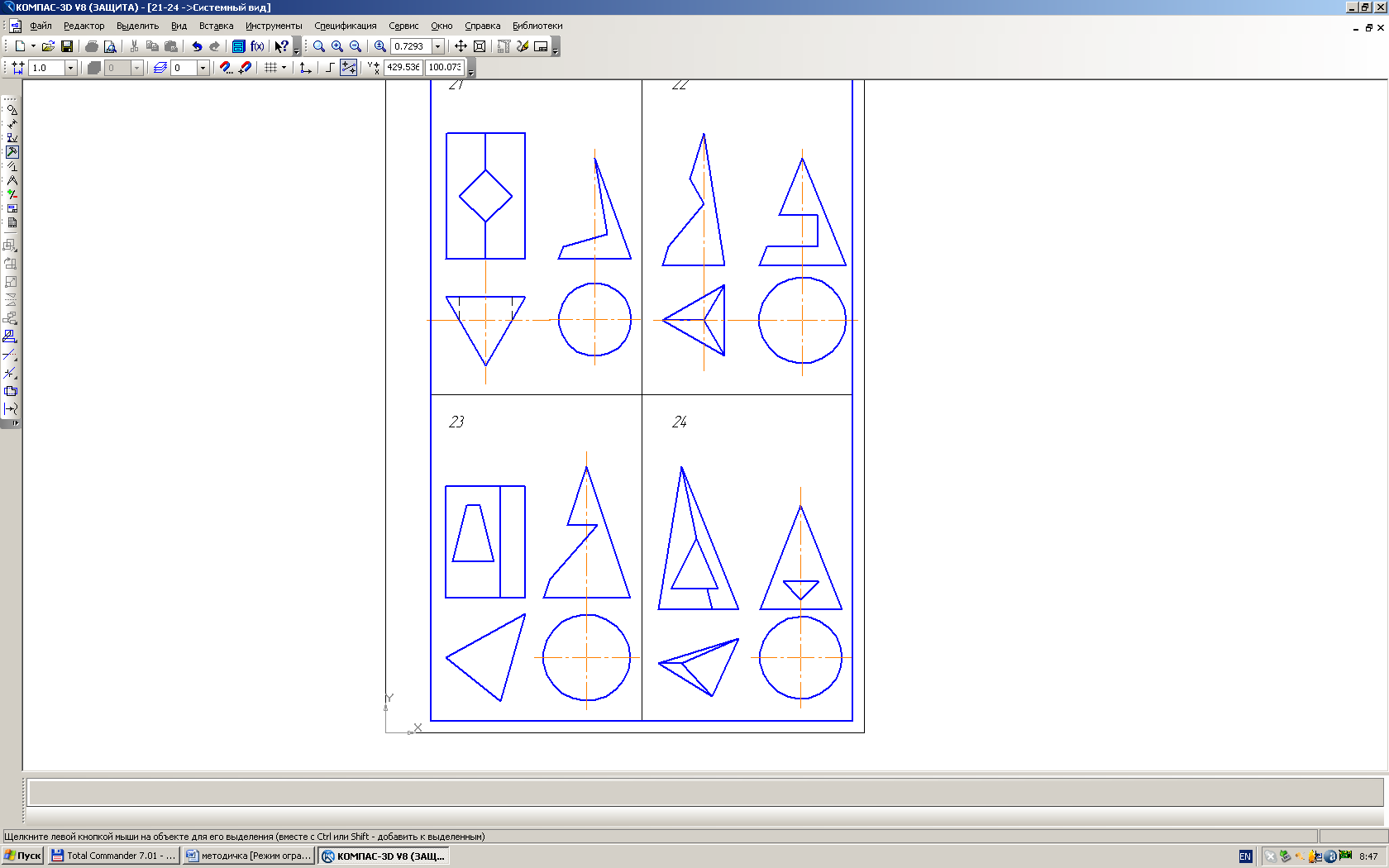
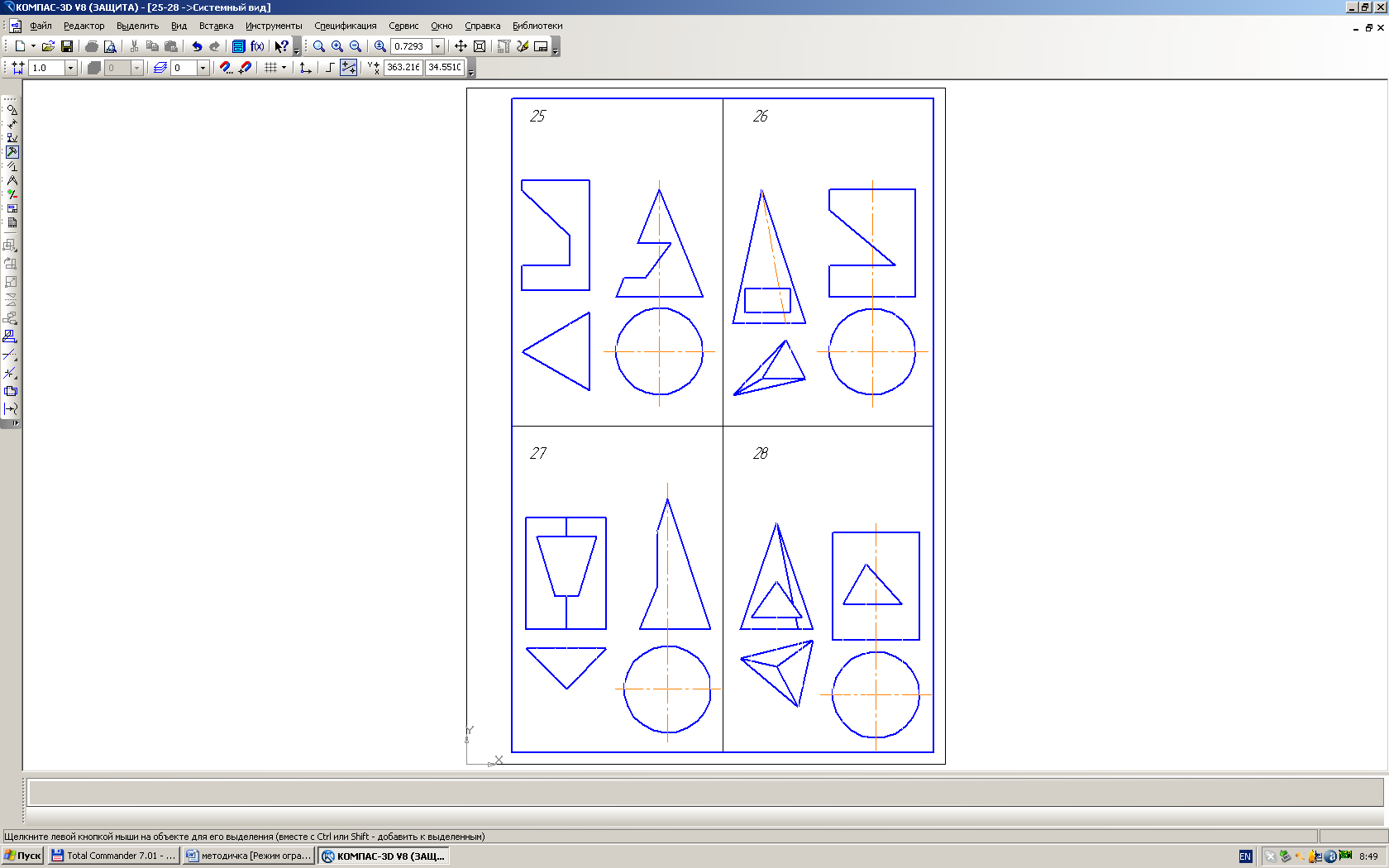
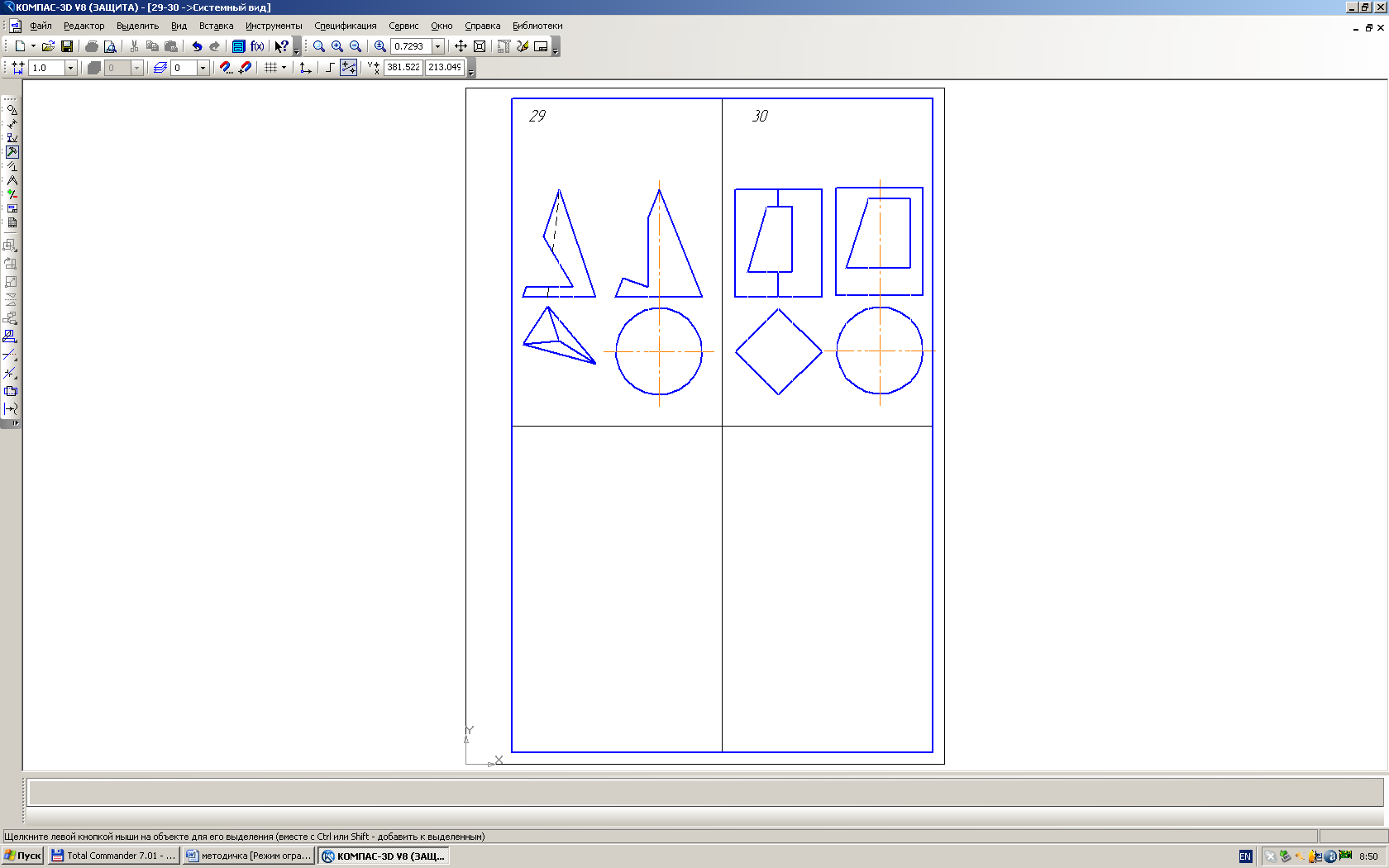
Лист 3-построить три проекции многогранника со сквозным отверстием. Выполнить аксонометрическое изображение этого многогранника.
Лист 4-построить три проекции тела вращения со сквозным отверстием и выполнить его аксонометрическое изображение
Варианты условий даны в табл. 3.
Пример решения задачи
Выполнение листа 3 начинаем с компоновки ф. А3. Решение задачи начинаем с горизонтальной проекции (рис. 4). Строим окружность Ø 80мм и вписываем в нее многоугольник (треугольник, квадрат, шестиугольник - в зависимости от заданного варианта). Для всех вариантов высота призмы или пирамиды равны 100 мм. При пересечении многогранника плоскостями, получаем плоские фигуры, которые называем многоугольником.
|
Рис. 4 |
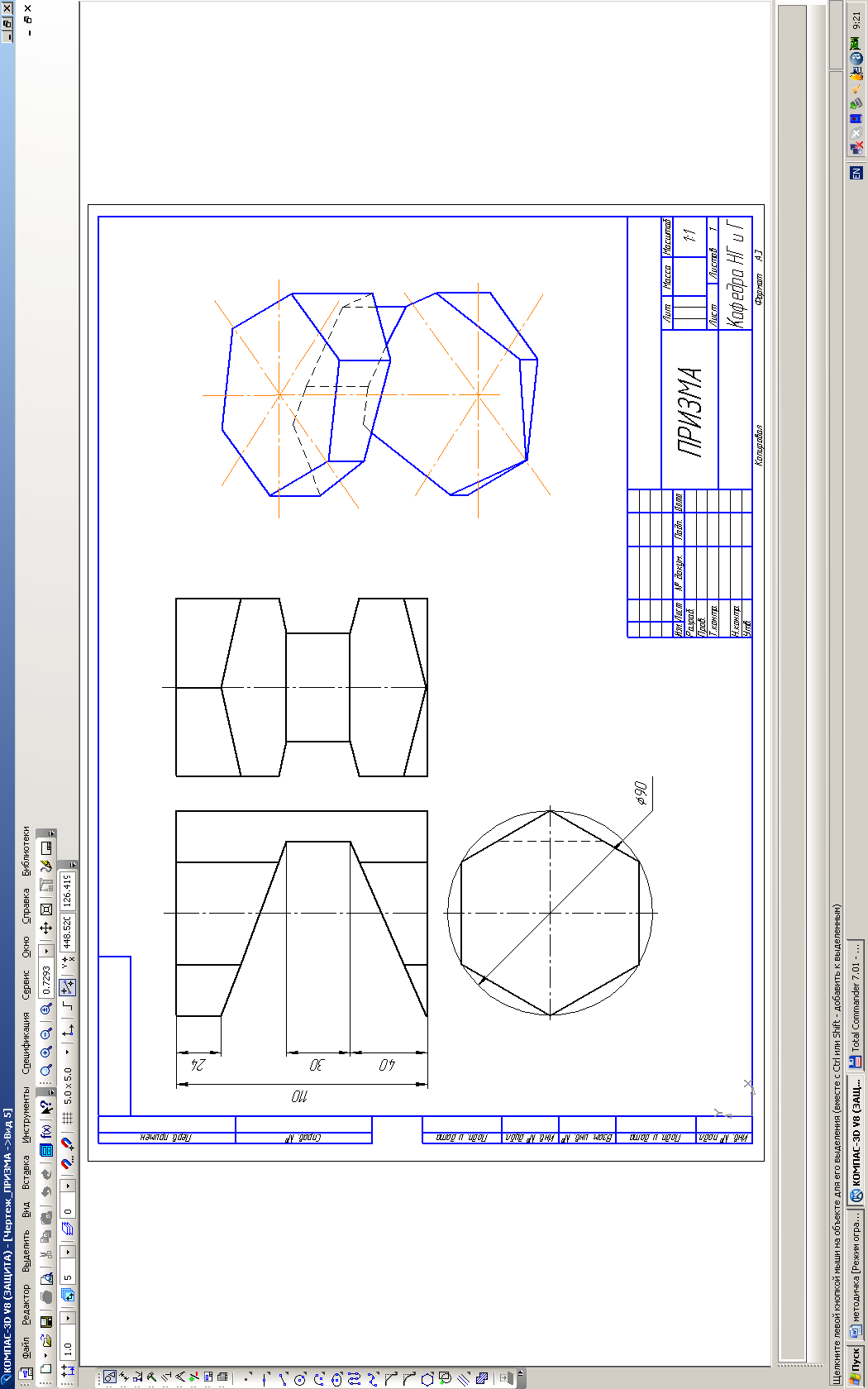
Причем вершины этих многоугольников принадлежат ребрам, а стороны – граням многогранника. Для построения проекций сквозных отверстий необходимо взять вспомогательные точки, которые принадлежат ребрам многогранника и ребрам отверстия. И находим их недостающие проекции. При выполнении наглядного изображения (аксонометрии) необходимо учитывать расположение ребер многогранника относительно осей координат. Если в призме или пирамиде в основании лежит четырехугольник, у которого вершины расположены на осях х и у, следовательно, аксонометрическое изображение следует выполнять в прямоугольной диметрии (более наглядно, чем изометрия).
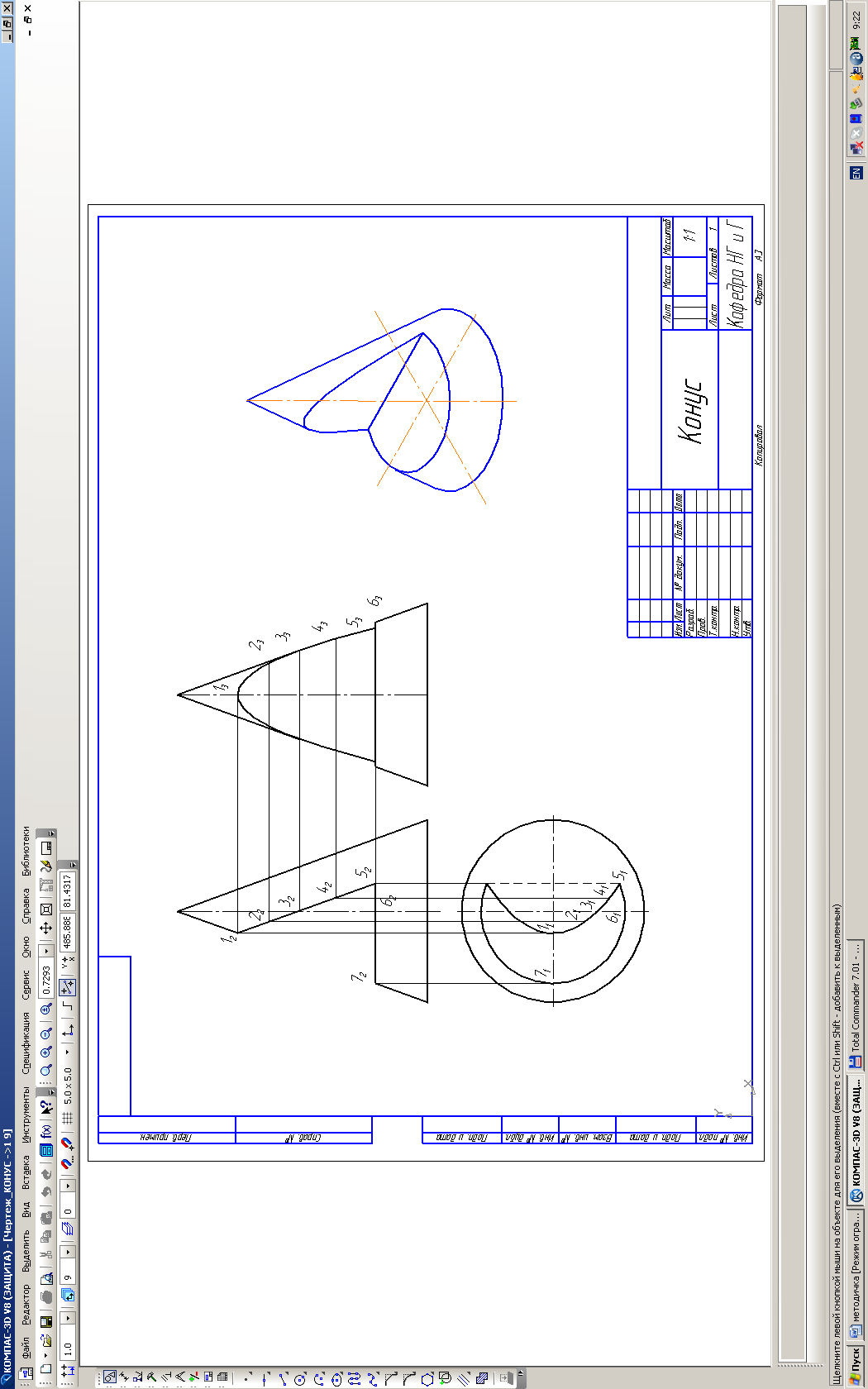
Лист 4. После компоновки ф-та А3 строим на горизонтальной проекции окружность Ø 80мм. Высота цилиндра или конуса равна 100 мм. Если задан прямой круговой конус со срезами, то необходимо вначале выучить раздел «Конические сечения». Построение кривых сечения конуса плоскостями выполняем с помощью вспомогательных линий (окружностей). Для построения кривых, принадлежащих фигуре сечения, берем на секущей линии не менее 4х вспомогательных точек и определяем их проекции ()горизонтальную и профильную). Для построения аксонометрического изображения следует изучить [4] стр. 127-147.
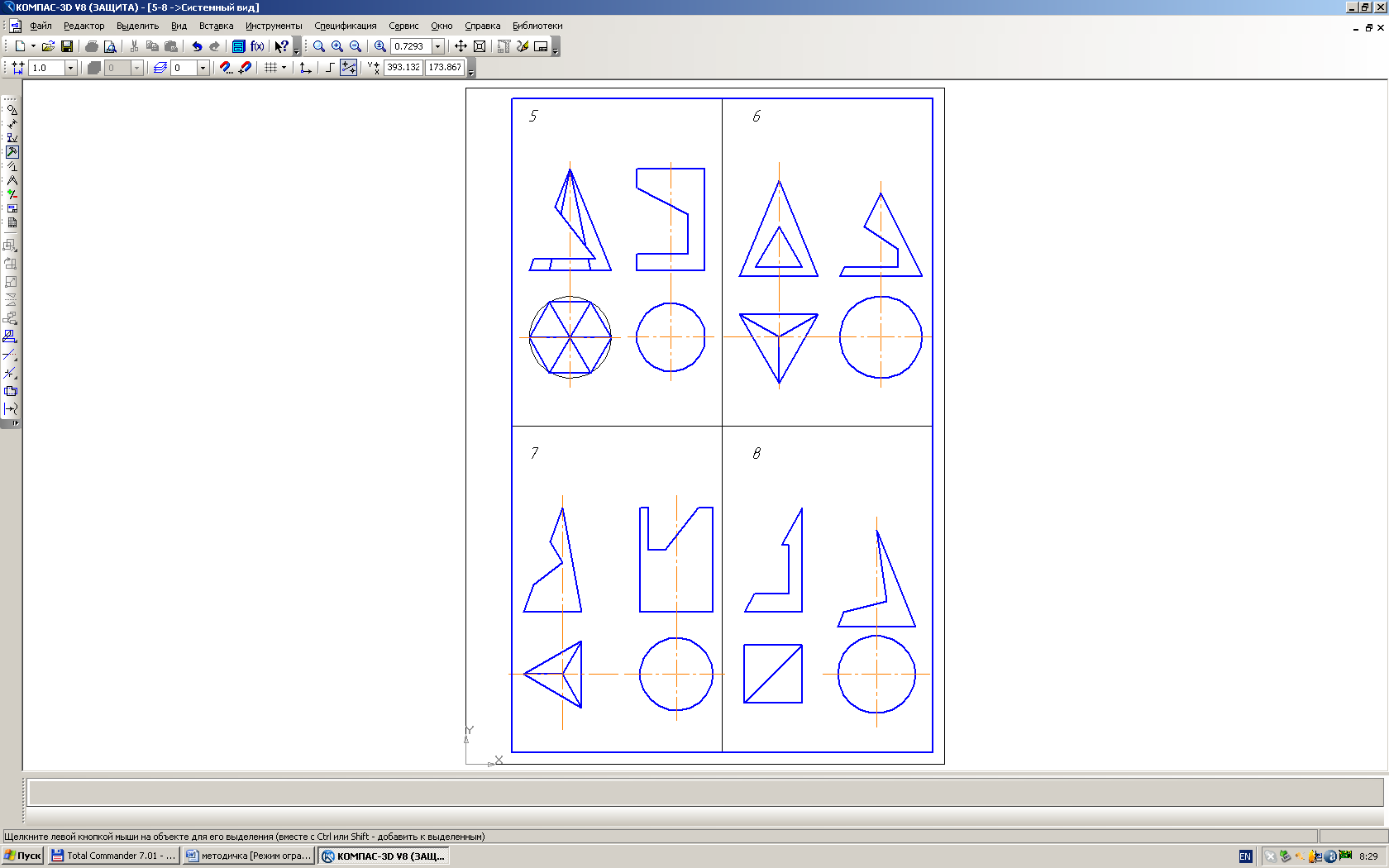
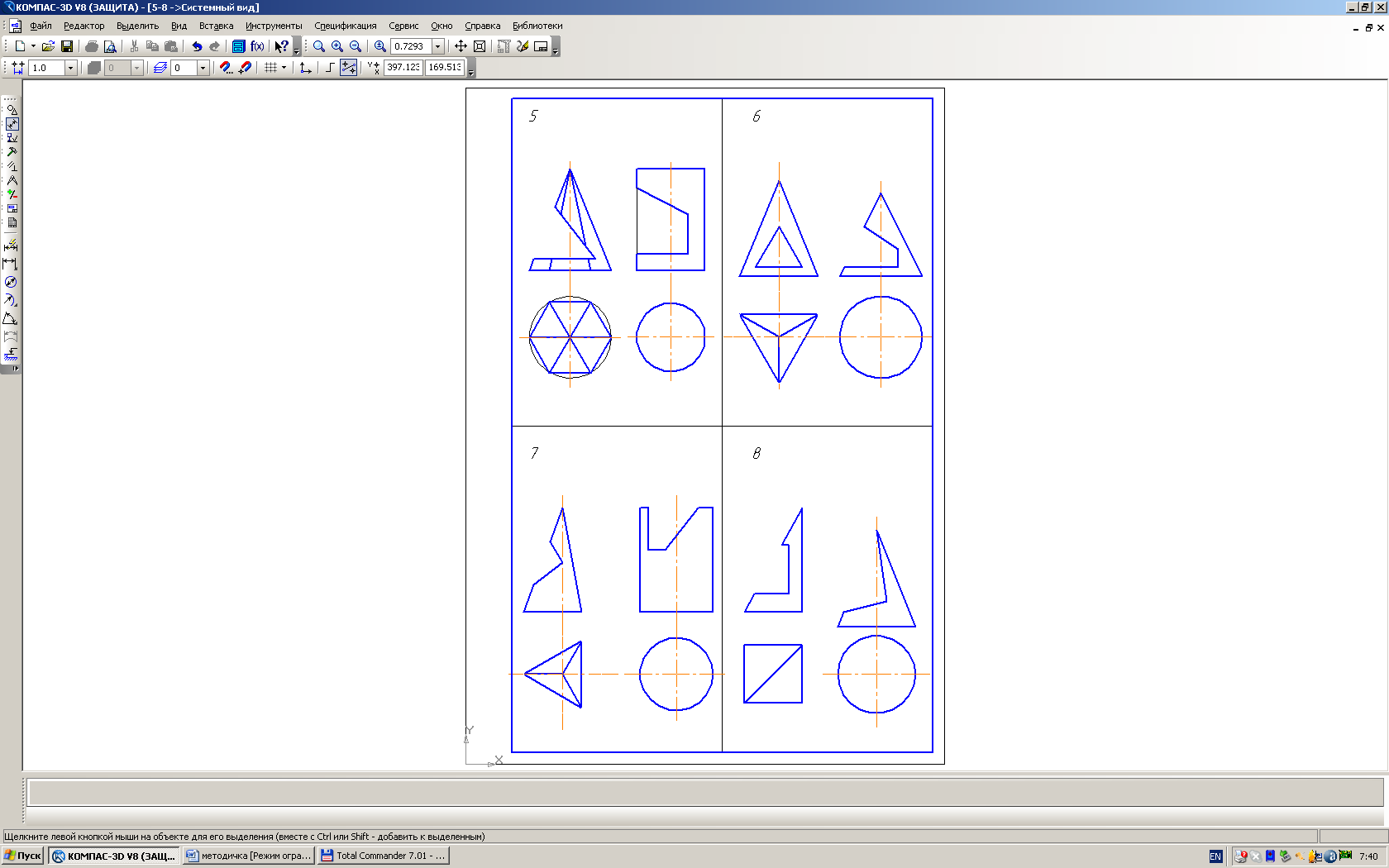
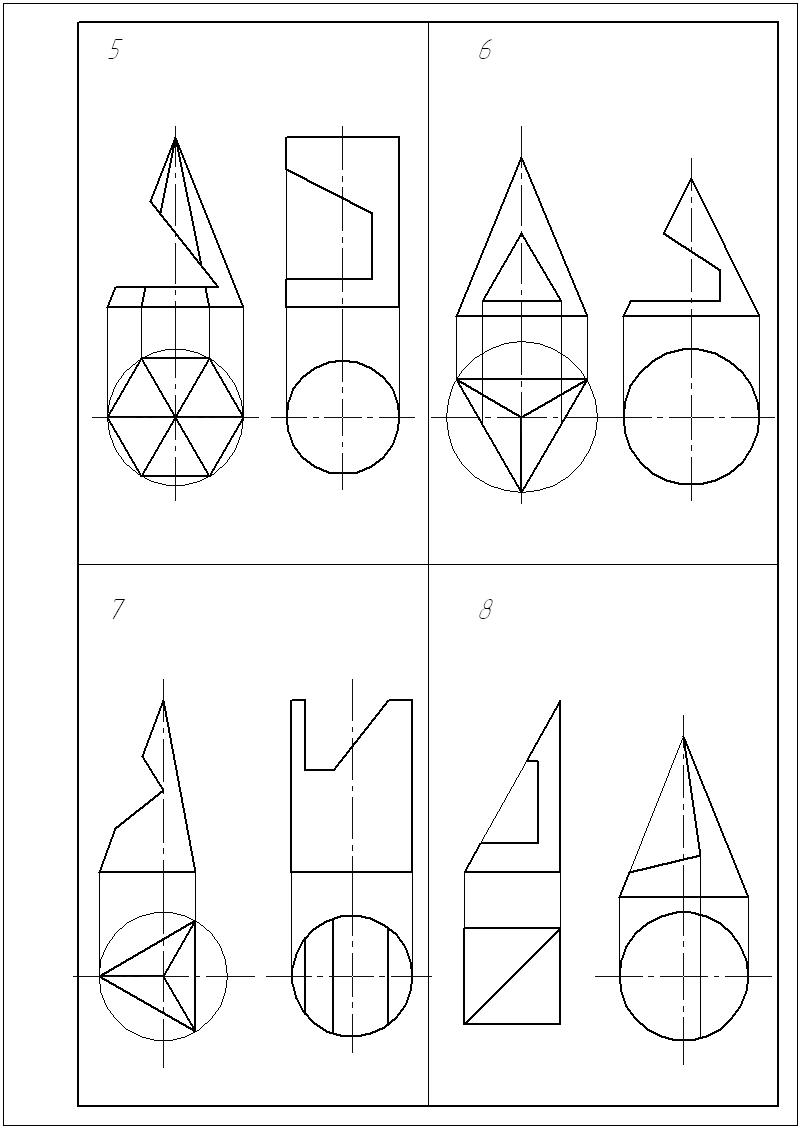
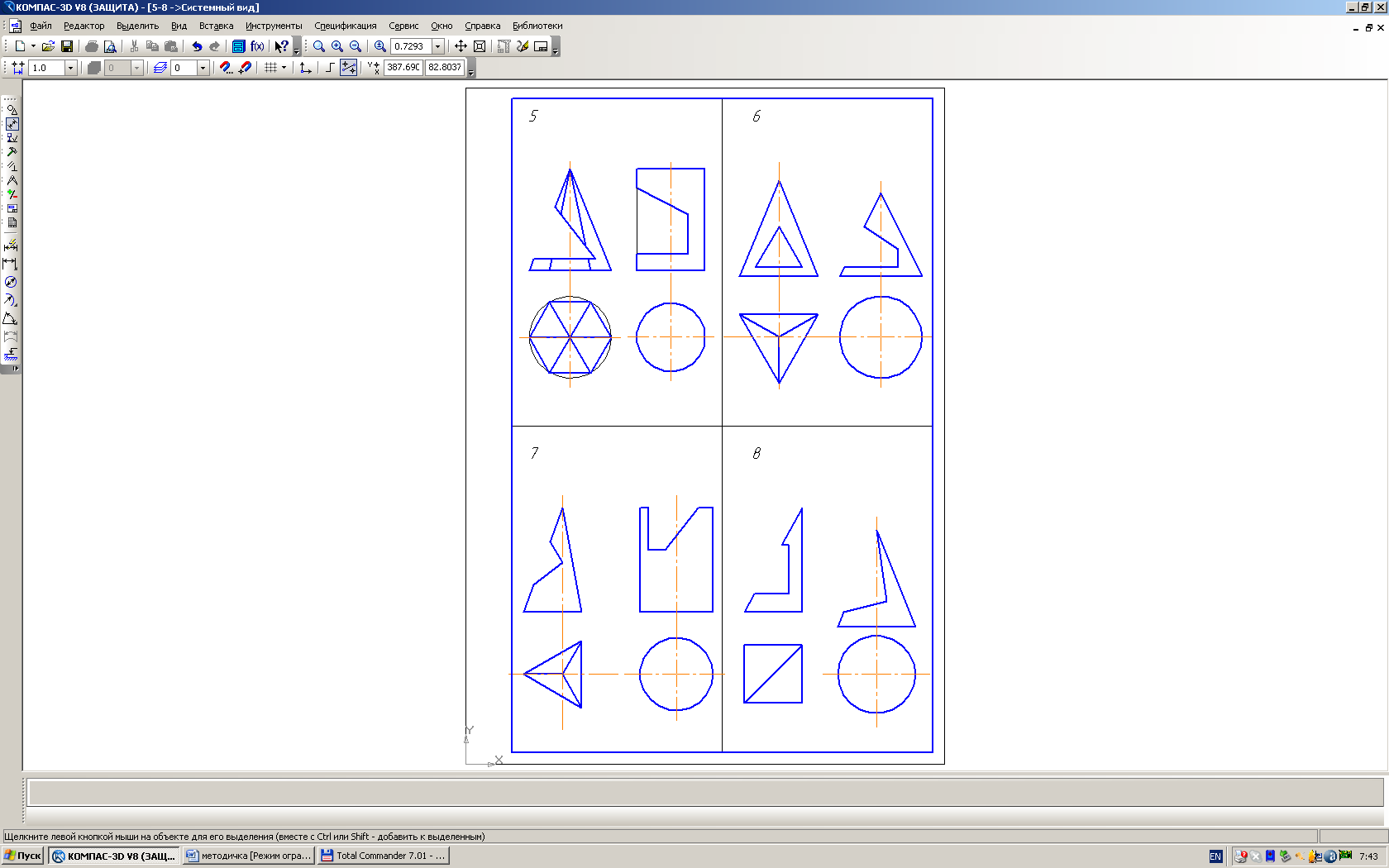
Примеры выполнения листов 3 и 4 приведены на рис. 5 и 6.
|
Рис. 5 |
|
Рис. 6 |
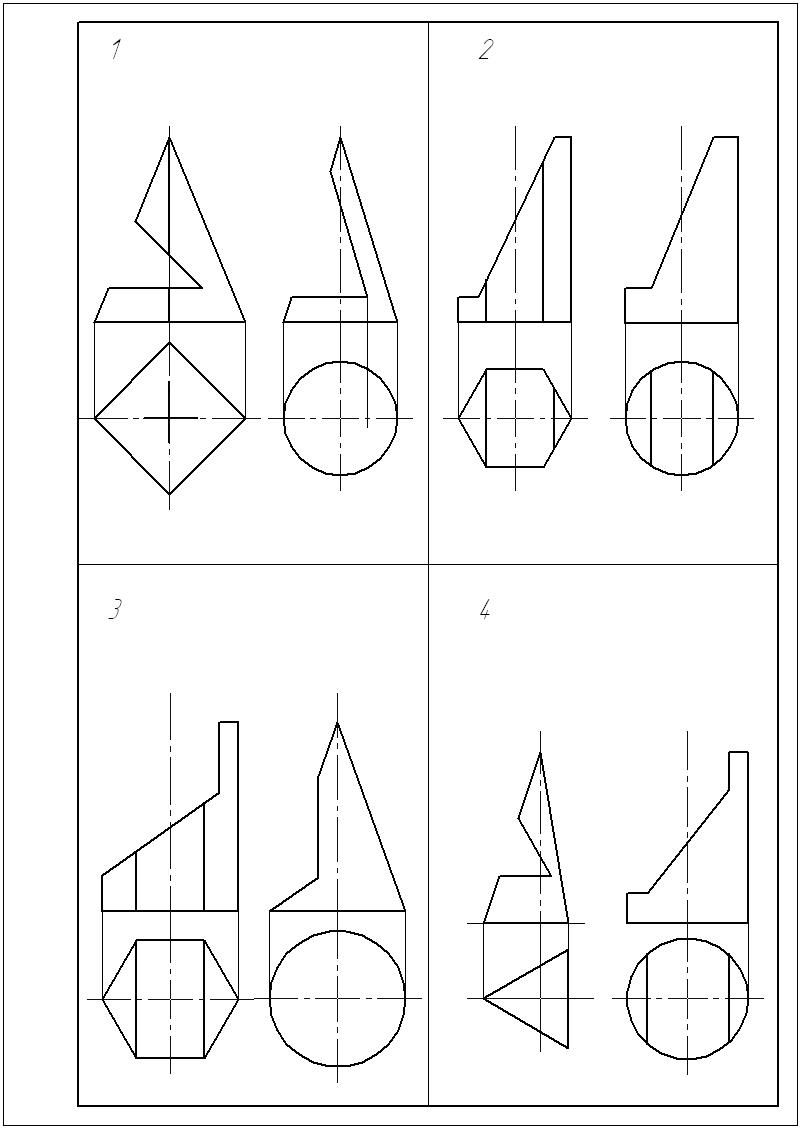
Таблица 3
|
|
ВАРИАНТ 1 |
ВАРИАНТ 2 |
|
|
ВАРИАНТ 3 |
ВАРИАНТ 4 |
|
|
ВАРИАНТ 5 |
ВАРИАНТ 6 |
|
|
ВАРИАНТ 7 |
ВАРИАНТ 8 |
|
|
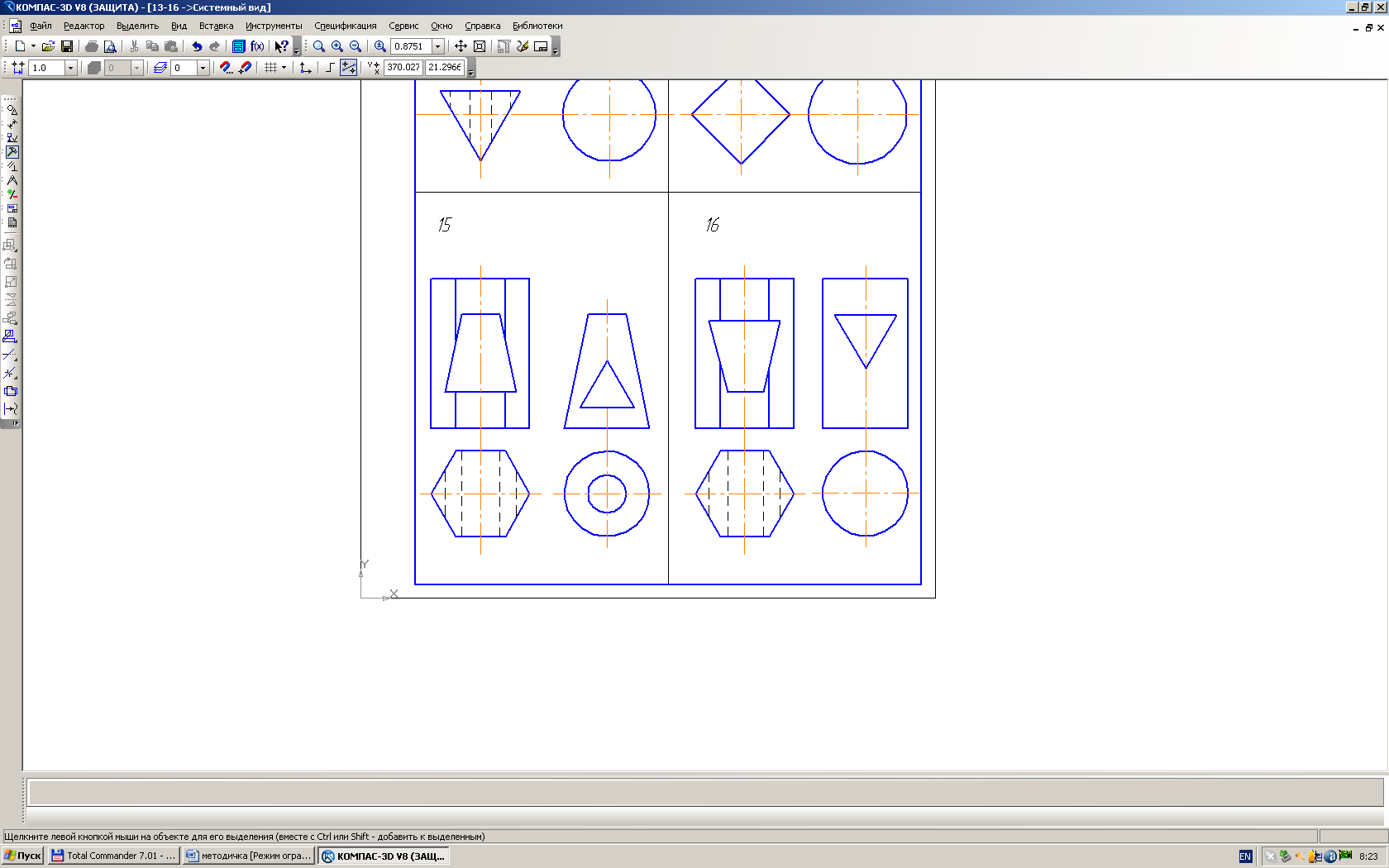
ВАРИАНТ 9 |
ВАРИАНТ 10 |
|
|
ВАРИАНТ 11 |
ВАРИАНТ 12 |
|
|
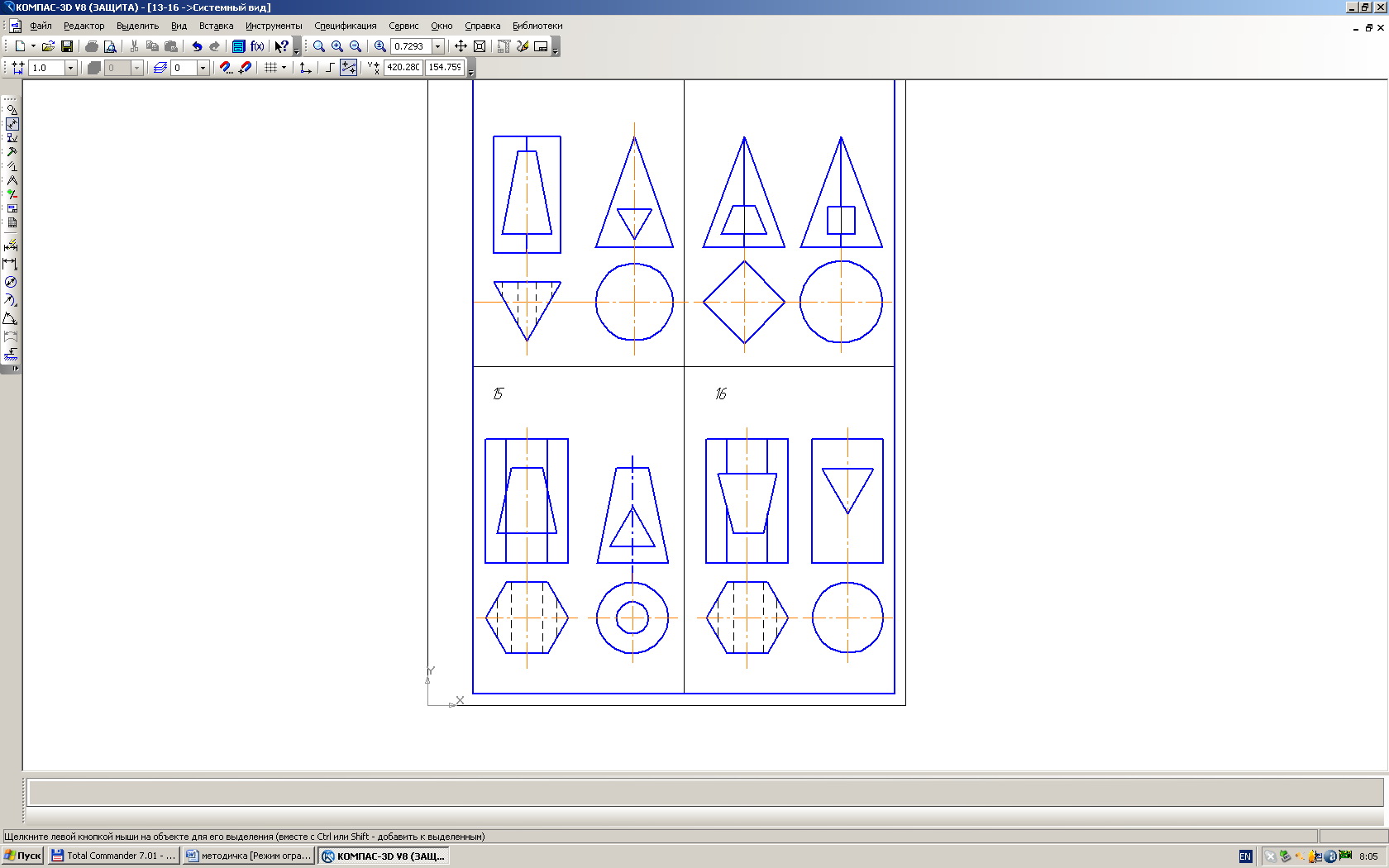
ВАРИАНТ 13 |
ВАРИАНТ 14 |
|
|
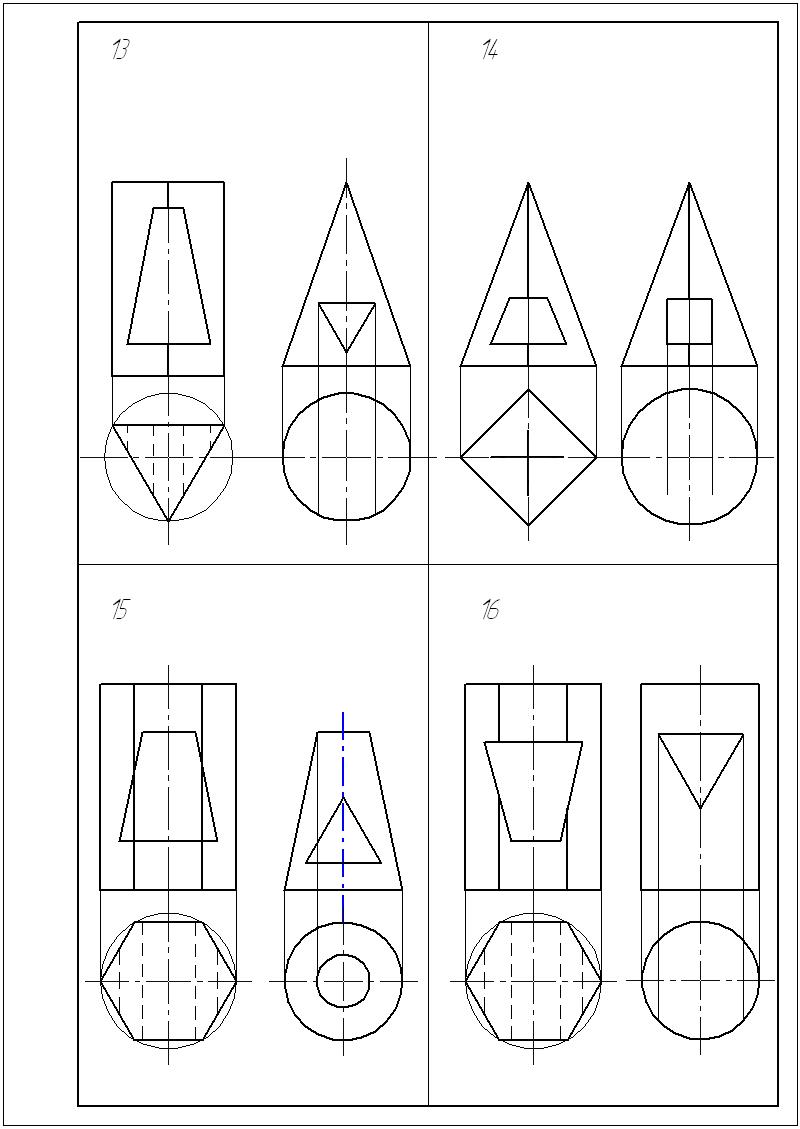
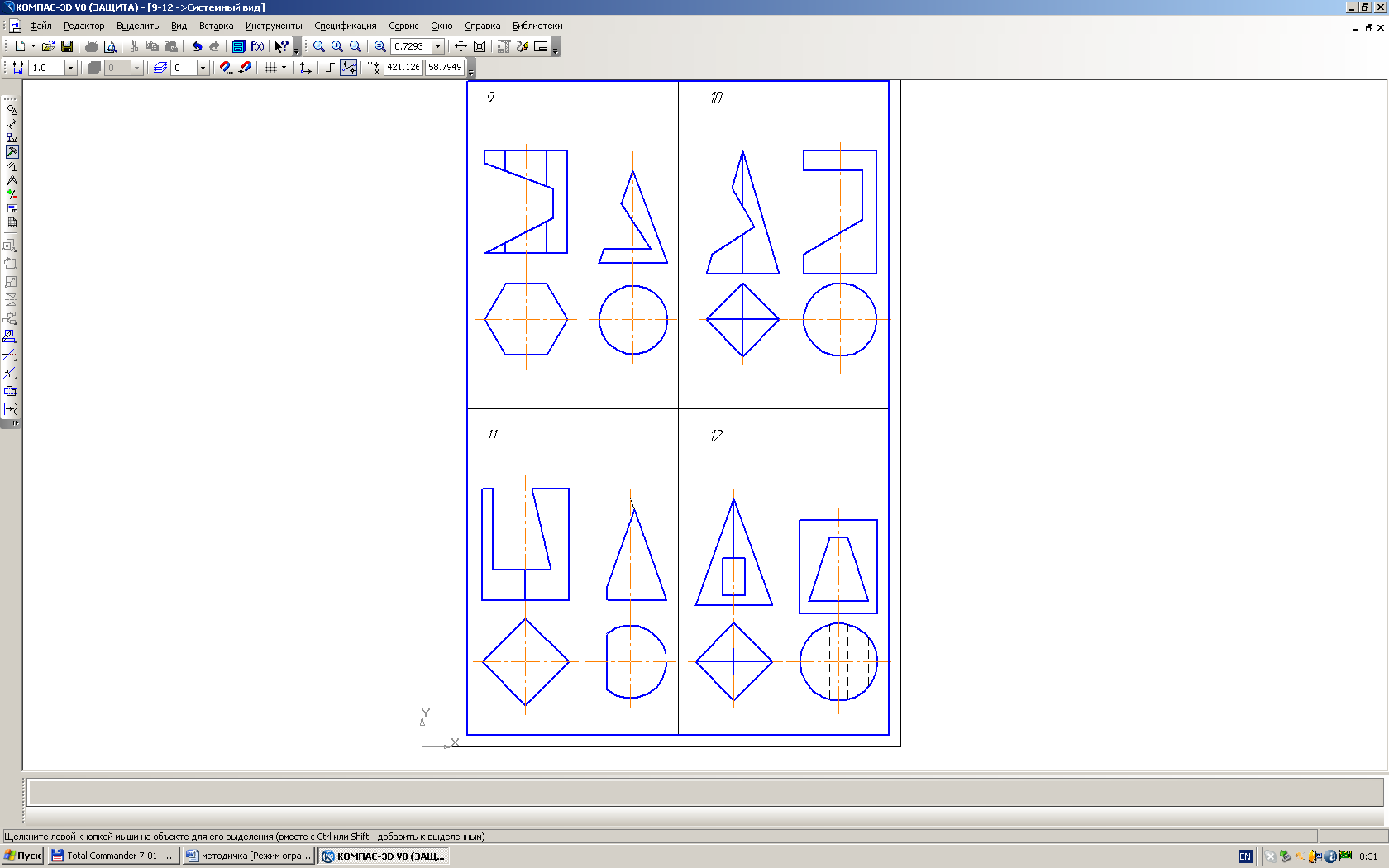
ВАРИАНТ 15 |
ВАРИАНТ 16 |
|
|
ВАРИАНТ 17 |
ВАРИАНТ 18 |
|
|
ВАРИАНТ 19 |
ВАРИАНТ 20 |
|
|
ВАРИАНТ 21 |
ВАРИАНТ 22 |
|
|
ВАРИАНТ 23 |
ВАРИАНТ 24 |
|
|
ВАРИАНТ 25 |
ВАРИАНТ 26 |
|
|
ВАРИАНТ 27 |
ВАРИАНТ 28 |
|
|
ВАРИАНТ 29 |
ВАРИАНТ 30 |
|
|
