Отображения и функции

Пусть заданы два множества А и В. Если для каждого элемента указан элемент , с которым сопоставляется а, то говорят, что между множествами А и В установлено соответствие.

Соответствие называется функциональным, если образом любого элемента из множества А является единственный элемент из множества В. График такого соответствия называется функциональным. Это означает, что в нем нет пар с одинаковыми первыми и различными вторыми компонентами.

Функциональное соответствие называется функцией.

Отображением называют всюду определенную функцию. Отображением множества А в множество В (функцией на А со значениями в В) называется правило, по которому каждому элементу множества А сопоставляется элемент множества В.

Т.к. понятие «функция» шире понятия «отображение», то в дальнейшем употребляется «функция».

Способы задания функций:

1 Аналитический. Аналитическим выражением называется символическое обозначение совокупности математических операций, которые производятся в определенной последовательности. Если обозначает аналитическое выражение, то функция задана аналитически, например Функция может иметь разные аналитические выражения на разных подмножествах множества Х, например:

2 Табличный. Функция определена таблицей своих значений или конечными списками пар.

Например:

	x	1	2	3	4	5	6	7
	y	9	7	9	7	6	3	2

В этом случае вычисление значений функции сводится к непосредственному считыванию соответствующих пар. Если необходимо знать значение функции для аргументов, отсутствующих в таблице, то его можно приблизительно вычислить при помощи правил интерполяции или экстраполяции.

3 Графический. Этот способ заключается в графическом изображении пар в выбранной системе координат.

4 Алгоритмический, типичным примером которого является рекурсивный способ. Рекурсивные процедуры задают функции следующим образом: заранее определено значение функции для одного или нескольких «начальных» значений аргумента, например (0) или (0) и (1). Значения функции при других аргументах определяются через ее значения в предыдущих точках. Как правило, рекурсивные процедуры задаются на множестве (подмножестве) натуральных чисел N. Например, функция n!: 1!=1; (m+1)!=m!(m+1). По определению 0!=1. Отличительной особенностью такого значения функции является то, что при вычислении значения функции для аргумента x=m, требуется предварительно вычислить значение функции во всех предыдущих точках. Для m! – это значения функции в точках 1, 2, 3, ..., m-1.

Т .к. в функциональной зависимости каждый элемент множества А связан с единственным элементом В, то в графических терминах функция описывается таким графом, у которого из каждой вершины, изображающей элементы множества А, выходит ровно одна стрелка.

Пример 8.

Рис.10

Пример 9. Определите, какие из следующих отношений между множествами

A={a, b, c}и B={1, 2,3}являются функциями из множества А в В.

Решение:

(а) Отношение – не функция, поскольку элементу а соответствуют два разных элемента множества В: 1 и 2.

(б) Отношение g является функцией.

(в) Последнее отношение функцией не является, поскольку элементу b не соответствует ни одного элемента.

Пример 10. Какие из отношений являются функциями?

(а) «х – брат или сестра у» на множестве всех людей;

(б) отношение на множестве Z, задано парами:

(в) отношение на множестве R, задано парами:

Решение:

(а) Это не функция, поскольку есть люди с несколькими братьями и сестрами, а также бывают семьи с единственным ребенком, т.е. ни брата, ни сестры нет.

(б) Отношение б функция, поскольку по каждому числу х его квадрата х² определяется однозначно.

(в) Последнее отношение – не функция, так как, например, обе упорядоченные пары: и - ему принадлежат. Кроме того, в нем отсутствуют пары (х, у) с отрицанием х.

Пусть – функция из множества А в множество В. Поскольку для каждого существует единственным образом определенный , такой, что , мы будем писать у = (х), и говорить, что функция отображает множество А в множество В, а (х) называть образом х при отображении или значением , соответствующим аргументу х.

Кроме того, можно написать :A→B, чтобы подчеркнуть, что функция переводит элементы из А в элементы В. Множество А принято называть областью определения, а В – областью значений функции .

Типы отображений. Отображение называется ее инъективным или инъекцией, или взаимно однозначным отображением, иначе «в», если для всех .

Это определение логически эквивалентно тому, что

т.е. у инъективной функции нет повторяющихся значений. Иными словами, разные входные данные дают различные выходные данные.

Будем называться функцию сюръективной или сюръекцией, или функцией «на», если множество ее значений совпадает с областью значений. Это означает, что для каждого найдется такой , что b= (a). Таким образом, каждый элемент области значений является образом какого – то элемента из области определения .

Мы называем биективной функцией или просто биекцией, если она как инъективна, так и сюръективна.

Пример 11. Определите, какие из функций, изображенных на рис. 11, инъективны, а какие сюръективны. Перечислите все биекции.

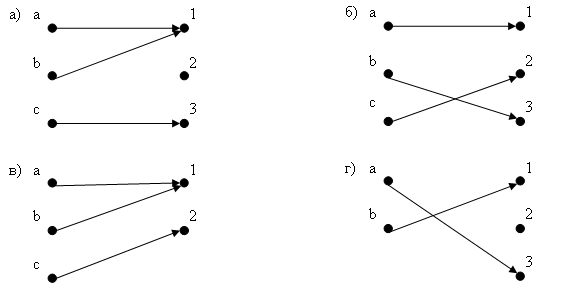
Рис.11

Решение:

(а) Данная функция не инъективна, поскольку значение 1 соответствует как a, так и b. Она не является и сюръекцией, ввиду того, что в элемент 2 ничего не переходит.

(б) Данная функция инъективна, т.к. не имеет повторяющихся значений. Она же и сюръективна, поскольку множество ее значений совпадает со своей областью значений.

(в) Значение 1 эта функция принимает как на а, так и на b. Следовательно, она не инъективна. Однако данная функция сюръективна, поскольку в ее множество значений входят все элементы области значений.

(г) Последняя функция инъективна, но не сюръективна (в элемент 2 ничего не переходит).

Только в случае (б) мы имеем биекцию.

Обратные функции. Пусть - произвольная функция. Рассмотрим функцию закон которой задан следующим образом: в том и только в том случае, если . Построенная таким образом функция называется обратной к функции . При графическом представлении обратная функция получается из данной переменной направления стрелок.

Если функция задана аналитически, например, у = 5х и требуется найти обратную, то следует:

1) выразить х через у;

2) переименовать переменные.

В соответствии с заданной функцией: 1)

2)

Таким образом, обратная функция будет .

Если функция задана перечислением пар, например, то для задания обратной функции следует пометь местами образы и прообразы, т.е.

Обратными для тригонометрических функций являются: для sin x - arcsin x,

для cos x – arcos x и т.д.

Для логарифмических функций обратной будет показательная и наоборот. Обратной для х² будет и т.д.

Обратная функция однозначна в том и только в том случае, когда заданная функция инъективна.

Функция обратима только тогда, когда она биективна.

Суперпозиция функций. Результатом суперпозиции двух данных функций и называется функция , закон которой задается следующим образом: в том и только в том случае, если существует такой элемент , что и .

Функция , полученная таким способом из функций и называется их композицией.

Пример 12. Даны две функции и (рис.12).

B

А

С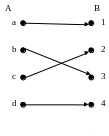

1

a

b

c

d

C

x

2

x

y

z

y

3

z

4

Рис.12

В функции в функции

В соответствии с определением получаем, что в новой функции

Пример 13. Заданы функции и Вычислить

Решение. Все четыре новые функции определены на R со значениями в R.

Как видно из вычислений, результат суперпозиции двух данных функций зависит от их порядка, т.е. операция суперпозиции не обладает свойством коммутативности.

В современных языках программирования функции используется очень широко. Они дают нам возможность выделить отдельные вычисления в подпрограммы. В большинстве языков есть специальные библиотеки с наиболее часто применяющимися функциями, такими как sin x, log x, и т.д. Кроме того, в них легко создавать собственные функции.

В некоторых особенно мощных языках, известных как языки функционального программирования, основные операторы определены в терминах функций. Главная особенность таких языков – возможность построения новых, более сложных, операторов из основных. Чтобы уметь это делать, нам необходимо в совершенстве овладеть композицией функций.