Дифференциал функции

Пусть функция y = f(x) дифференцируема в точке х₀.

Тогда ее приращение можно записать:

, где (х)0, при х0.

Величина (x) является бесконечно малой, а слагаемое является линейной функцией от x и составляет главную часть приращения функции.

Дифференциалом функции f(x) в точке х₀ называется линейная относительно x функция , составляющая главную часть приращения функции в точке х₀.

Обозначается df(х₀) или dy.

dy = f(x)dx.

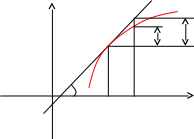
Геометрический смысл дифференциала

y

f(x)

K

dy

M y

L



x₀ x₀ + x x

Из треугольника MKL: KL = dy = tgx = yx

Таким образом, дифференциал функции f(x) в точке х₀ равен приращению ординаты касательной к графику этой функции в рассматриваемой точке.

Свойства дифференциала

Если u = f(x) и v = g(x)- функции, дифференцируемые в точке х, то непосредственно из определения дифференциала следуют следующие свойства:

1. d(u  v) = (u  v)dx = udx  vdx = du  dv

2. d(uv) = (uv)dx = (uv + vu)dx = vdu + udv

3. d(Cu) = Cdu

4. 

Пример. Найти дифференциал функции .

Сначала преобразуем данную функцию: , найдем производную

Тогда дифференциал будет равен

Пример. Найти дифференциал функции .

Сначала найдем производную:

Тогда дифференциал будет равен

Пример. Найти дифференциал функции

Пример. Найти дифференциал функции

Пример. Найти дифференциал функции

Приближенные вычисления с помощью дифференциала

1. Вычисление приближенного значения приращения функции

Пример. Пользуясь понятием дифференциала функции, вычислить приближенно изменение функции при изменении аргумента от 5 до 5,01.

Найдем дифференциал функции . Подставим значения х₀ = 5, х = 0,01. Получим

2. Вычисление приближенного значения функции

Пример. Вычислить приближенное значение с помощью дифференциала 1,998⁵.

Рассмотрим функцию , где х = 1,998. Разобьем х на х₀ и х (х = х₀ + х), пусть х₀ = 2, тогда х = - 0,002.

Найдем значение , ,

Тогда 1,998⁵  32 – 0,16 = 31, 84.

Производные и дифференциалы высших порядков

Пусть функция f(x)- дифференцируема на некотором интервале. Тогда, дифференцируя ее, получаем первую производную

Если найти производную функции f(x), получим вторую производную функции f(x).

т.е. y = (y) или .

Этот процесс можно продолжить и далее, находя производные степени n.

.

Основные теоремы дифференциального исчисления

1. Теорема Ролля. Если функция f(x) непрерывна на отрезке [a, b], дифференцируема в интервале (а, b) и значения функции на концах отрезка равны f(a) = f(b), то в интервале (а, b) существует хотя бы одна точка c (a < c < b), в которой производная f '(с) = 0.

Геометрический смысл теоремы Роля. Геометрический смысл теоремы Ролля состоит в том, что при выполнении условий теоремы на интервале (a, b) существует точка с такая, что в соответствующей точке кривой y = f(x) касательная параллельна оси Ох. Таких точек на интервале может быть и несколько, но теорема утверждает существование по крайней мере одной такой точки.

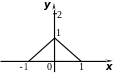
Заметим, что если хотя бы в одной точке промежутка [a; b] функция не дифференцируема, то производная функции f (x) может в нуль и не обратиться. Например, функция y =1-xнепрерывна на промежутке [-1; +1], дифференцируема в (-1;+1) за исключением точки x₀ = 0, причем  f (-1) = f (1) = 0, т.е. условие теоремы Ролля нарушено в единственной точке x₀ = 0 (в ней функция не дифференцируется). Очевидно, что ни в одной точке графика функции на промежутке [-1; 1] касательная к графику не параллельна оси 0x.

Теорема Ролля имеет несколько следствий:

1. Если функция f(x) на отрезке [a, b] удовлетворяет теореме Ролля, причем f(a) = f(b) = 0, то существует, по крайней мере, одна точка с, a < с < b, такая, что f(с) = 0. Т.е. между двумя нулями функции найдется хотя бы одна точка, в которой производная функции равна нулю.

2. Если на рассматриваемом интервале (а, b) функция f(x) имеет производную (n-1)-го порядка и n раз обращается в нуль, то существует, по крайней мере, одна точка интервала, в котором производная (n –1)–го порядка равна нулю.

2. Теорема Лагранжа. Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема в интервале (а, b), то в этом интервале найдется, по крайней мере, одна точка c (a < c < b), такая, что .

Это означает, что если на некотором промежутке выполняются условия теоремы, то отношение приращения функции к приращению аргумента на этом отрезке равно значению производной в некоторой промежуточной точке.

Рассмотренная выше теорема Ролля является частным случаем теоремы Лагранжа.

Выражение называется формулой конечных приращений Лагранжа.

Геометрический смысл теоремы Лагранжа.

Пусть выполнены условия теоремы Лагранжа, тогда справедлива формула конечных приращений Лагранжа.

Пусть точки A и B, лежащие на графике функции, имеют координаты A (a; f (a)), B (b; f (b)), тогда очевидно, что величина дроби равна тангенсу угла наклона хорды AB к оси Оx, т.е. .

С другой стороны, f '(c) = tg. Значит, в точке x = c касательная к графику функции y = f (x) параллельна хорде, стягивающей дугу кривой AB. В этом и заключается геометрический смысл теоремы Лагранжа.

3. Теорема Коши. Если функции f(x) и g(x) непрерывны на отрезке [a, b] и дифференцируемы в интервале (a, b) и g(x)  0 ни в одной точке этого интервала, то существует по крайней мере одна точка c (a  c  b), такая, что имеет место равенство:

.

Т.е. отношение приращений функций на данном отрезке равно отношению производных в точке с.

Геометрический смысл теоремы Коши.

Нетрудно убедиться в том, что геометрический смысл теоремы Коши совпадает с геометрическим смыслом теоремы Лагранжа.