§ 5. Метод комплексных амплитуд

Используется при расчете более сложных цепей.

Вместо действительных величин – напряжения и тока, меняющихся по гармоническому закону, используются комплексные функции.

В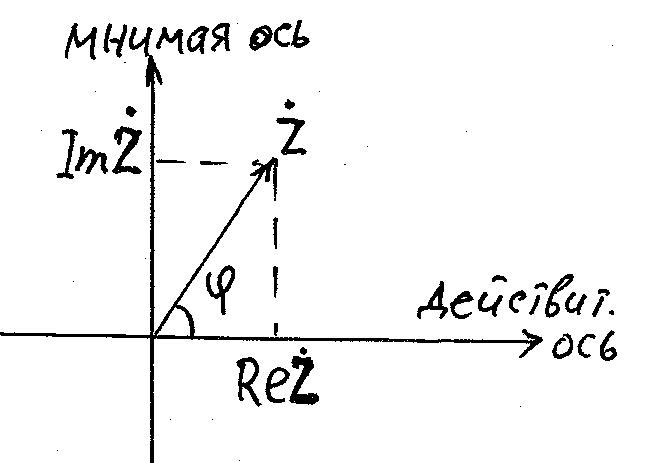 спомним, что комплексное число (точкой над буквой будем подчеркивать ее комплексный характер) состоит из действительной и мнимой частей. Его можно представить как вектор на плоскости. Длина вектора равна модулю числа (Z), угол – это фаза числа: (i – мнимая единица). Формула Эйлера: ; , .

Силе тока ставится в соответствие комплексная функция . Физический смысл имеет действительная часть этой функции . Напряжению ставится в соответствие комплексная функция . Физический смысл имеет действительная часть этой функции .

Комплексное сопротивление (или импеданс) вводят так, чтобы выполнялся закон Ома для мгновенных значений и : . Таким образом,

. (1)

Модуль комплексного сопротивления равен полному сопротивлению цепи Z - он связывает амплитудные (или действующие) значения напряжения и силы тока. Аргумент комплексного сопротивления показывает, на сколько напряжение опережает по фазе ток.

Итак, комплексное сопротивление, в отличие от действительного сопротивления , несет информацию не только об отношении амплитудных (или действующих) значений напряжения и силы тока, но и о разности фаз между током и напряжением в цепи.

Удобство работы с комплексными функциями состоит в том, что закон Ома справедлив для мгновенных значений и , поэтому для расчета можно использовать те же алгоритмы, что в цепях постоянного тока. Так, при последовательном соединении участков цепи их комплексные сопротивления складываются, а при параллельном соединении складываются обратные сопротивления.

Найдем сначала комплексные сопротивления индуктивности и емкости.

На индуктивности напряжение опережает ток на , поэтому комплексное сопротивление индуктивности

На емкости напряжение отстает от тока на , поэтому комплексное сопротивление емкости

Итак:

(2).

(3).

На активном сопротивлении разность фаз между током и напряжением равна нулю, поэтому оно остается вещественным и равным .

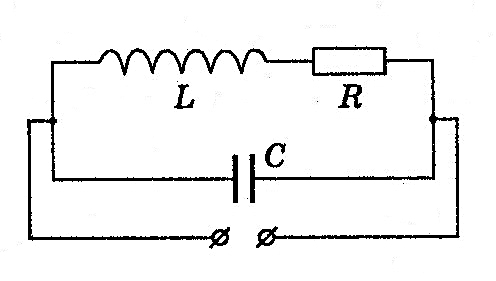
Рассмотрим в качестве примера цепь, состоящую из двух параллельных ветвей: одна ветвь содержит конденсатор, и ее комплексное сопротивление равно ; вторая ветвь включает последовательно соединенные индуктивное и активное сопротивления, поэтому ее комплексное сопротивление равно . Комплексное сопротивление всей цепи равно

.

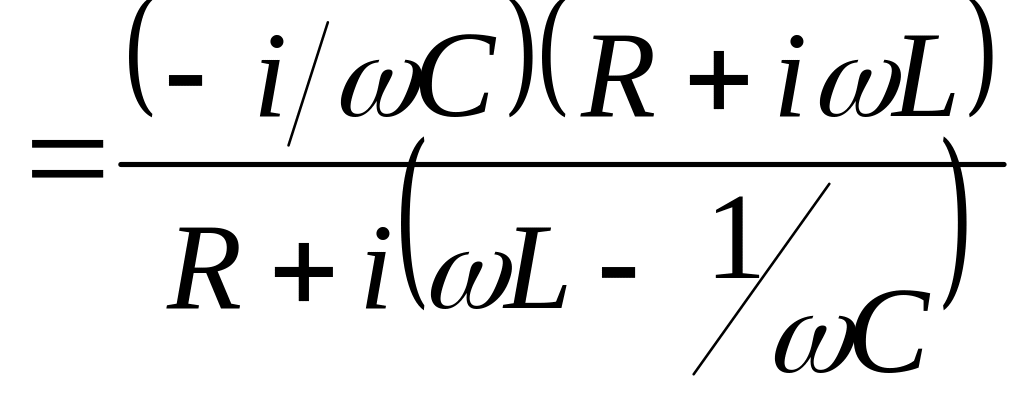
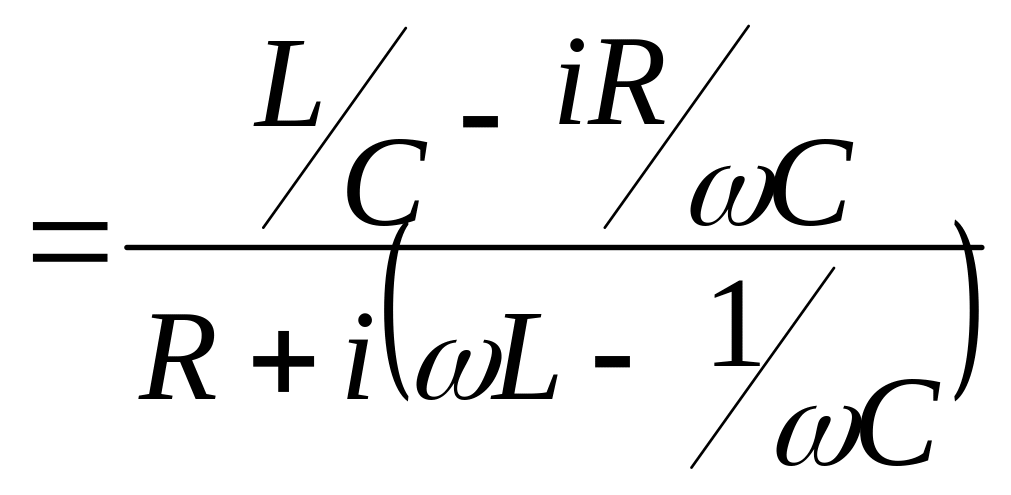Полное сопротивление Z равно модулю полученного числа. Модуль дроби равен отношению модулей числителя и знаменателя, поэтому

.

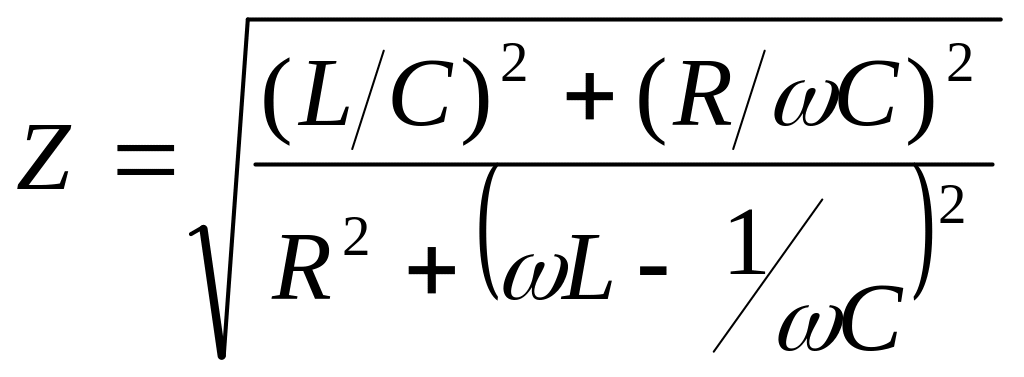Чтобы найти фазу , надо у комплексного числа выделить действительную часть. Тогда .

§ 6. Мощность в цепи переменного тока

Мгновенная мощность, потребляемая участком цепи, равна произведению мгновенных значений напряжения и силы тока:

.

Учтем, что , поэтому

.

Интерес представляет средняя за большой промежуток времени мощность Р. Усредним полученное выражение. Учитывая, что , , получим:

Средняя мощность , потребляемая цепью переменного тока, определяется действующими значениями напряжения и тока и разностью фаз между ними. Число называют коэффициентом мощности.

Рассчитать среднюю мощность на участке цепи можно двумя способами.

1 способ. Вычислить сопротивление цепи и .

. (1)

2 способ. Хотя потребляемая цепью мощность зависит от всех параметров цепи, выделяется средняя мощность (в виде теплоты) только на активном сопротивлении. Реактивные элементы цепи (емкость и индуктивность) в течение половины периода запасают энергию, в течение другой половины периода отдают ее обратно источнику, так что в среднем мощности не потребляют. Поэтому для вычисления средней мощности достаточно знать действующую силу тока , текущего через активное сопротивление. По закону Джоуля-Ленца (и с учетом того, что на активном сопротивлении напряжение и ток изменяются в фазе) выделяемая тепловая мощность равна

(2).

Итак, этот способ требует вычисления только силы тока через активную нагрузку (поэтому он, как правило, короче).

П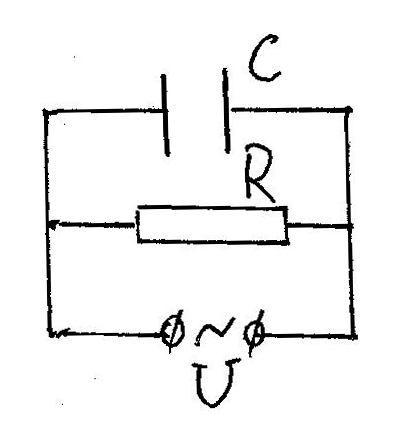 ример. Действующее значение тока через резистор , поэтому контур потребляет среднюю мощность .

Демонстрация. Подключая ваттметр поочередно к конденсатору, катушке и резистору, измеряем потребляемую ими среднюю мощность: , , .