2.1.2 Резонансные кривые для тока

Из закона Ома (48) видно, что при ω→0 и ω→∞ i₀→0.

При

(52)

амплитуда тока достигает своего максимального знамения

(53)

Итак, (52) есть условие резонанса для тока, откуда для резонансной частоты ω_ip получаем

(54)

Резонансные кривые для тока i₀(ω) при постоянной амплитуде эдс источника ε₀ и заданных параметрах L и С приведены на рис. 6(б). Из формулы (53) и рисунка 6(б) видно, что при увеличении R амплитуда тока уменьшается и резонанс

выражен менее отчетливо. Однако резонансная частота не зависит от активного сопротивления и равна ω₀.

При вынужденных колебаниях в контуре кроме рассмотренного нами резонанса напряжения на конденсаторе и резонанса тока имеет место резонанс и других изменяющихся со временем величин: q(t), ε_L(t), U_R(t). Но все эти явления резонанса, происходящие в последовательном контуре, т.е. когда источник напряжения и все элементы контура соединены последовательно, называются резонансом напряжений, в отличие от случаев, когда источник ЭДС подключается к контуру параллельно. В этих случаях наблюдается резонанс токов, который в данной работе не рассматривается.

1.1.4.Определение добротности контура при вынужденных

Колебаниях

Добротность при вынужденных колебаниях определяет амплитуду напряжения на конденсаторе в резонансе. Действительно, из (43) имеем:

(55)

При не очень большом сопротивлении, полагая и учитывая (32), преобразуем выражение (55)

или

(56)

Т.е. добротность колебательного контура показывает, во сколько раз резонансная амплитуда напряжения на конденсаторе больше амплитуды вынуждающей ЭДС. Аналогично можно определить амплитуду напряжения на индуктивности L.

(57)

Таким образом, амплитудные значения U_0L и U_0C при резонансе равны по величине, но согласно (47), находятся в противофазах, поэтому их суммарное значение равно нулю. Отсюда и .название – резонанс напряжений. При резонансе величина тока определяется

лишь падением напряжения на активном сопротивлении, т.е. как и следовало ожидать.согласно (53).

Добротность характеризует также и ширину резонансной кривой, или полосы пропускания данного контура. Это чрезвычайно важно для настройки контура на определенную частоту.

Чтобы это показать, построим резонансную кривую U_C=f(ω) в безразмерных координатах. По ординате отложим 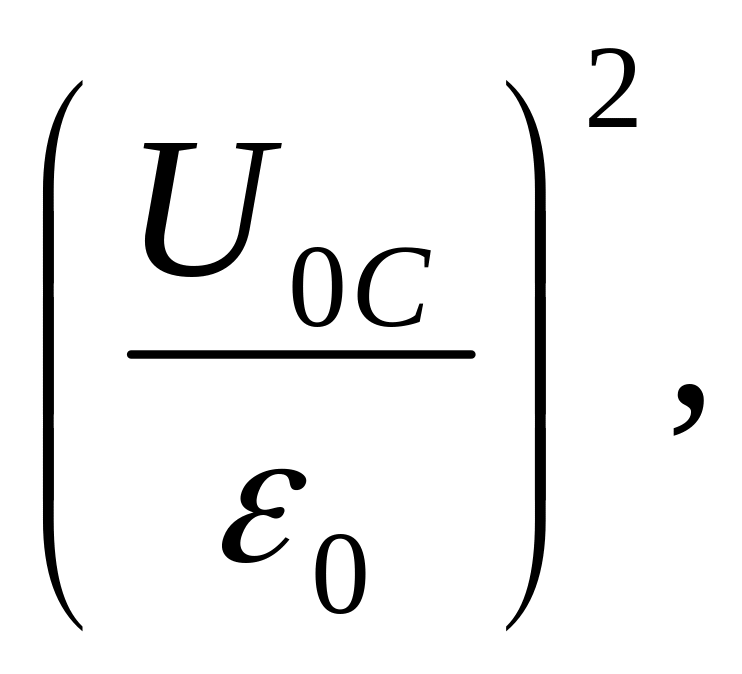а по абсциссе отношение (рис.7). Из (49), используя (5),

Найдем

или (58)

где Q – добротность контура (32).

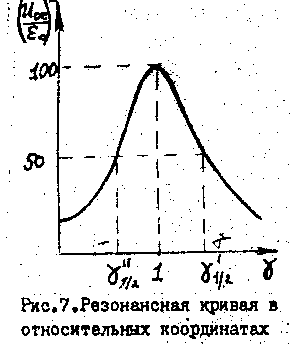
Если теперь найти значение γ=γ_1/2, при котором величина вдвое меньше резонансной величины, т.е.

то выражение (58) можно записать

Или

(59)

Решая уравнение (59) ; находим, что

(60)

Рассмотрим, контуры с большой добротностью (Q>>1), членами порядка 1/Q² можно пренебречь, и из (60) получим

или

(61)

Из (61) видно, что существуют два значения γ_1/2, расположенные по обе стороны максимума резонансной кривой (γ=1), при которых величина в два раза меньше своего максимального значения. Обозначив эти значения через γ’_1/2 и γ’’_1/2, из (57) имеем

и

отсюда,

ИЛИ

(62)

Разность γ’_1/2 γ’’_1/2 называют полосой пропускания или полушириной резонансной кривой. Чем выше добротность контура, тем меньше полоса пропускания, тем лучше избирательность контура.

Примечание: Полуширину резонансной кривой можно рассчитать и из зависимости U_C(ν). Для этого нужно провести горизонтальную линию на уровне и спроектировать точки пересечения на ось ν. Тем самым мы получим ν’_1/2 и ν’’_1/2. Т.е.

(63)