
- •Вариант 11
- •Вариант 12
- •Анықтауыштардың дәрежесін төмендетіп есептеу керек (Вычислить определители методом понижения порядка):
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •4. Матрица рангісін анықта (Определить ранг матриц):
- •6. Теңдеулер жүйесін Гаусс әдісімен шеш:
Вариант 11
Анықтауыштардың дәрежесін төмендетіп есептеу керек (Вычислить определители методом понижения порядка):
а)
 б)
б) .
Жауабы(Отв.): а)360, б)54
.
Жауабы(Отв.): а)360, б)54
С=2AB+3E матрицасын тап, егер (Найти матрицу С=2AB+3E, если):
![]() ,
,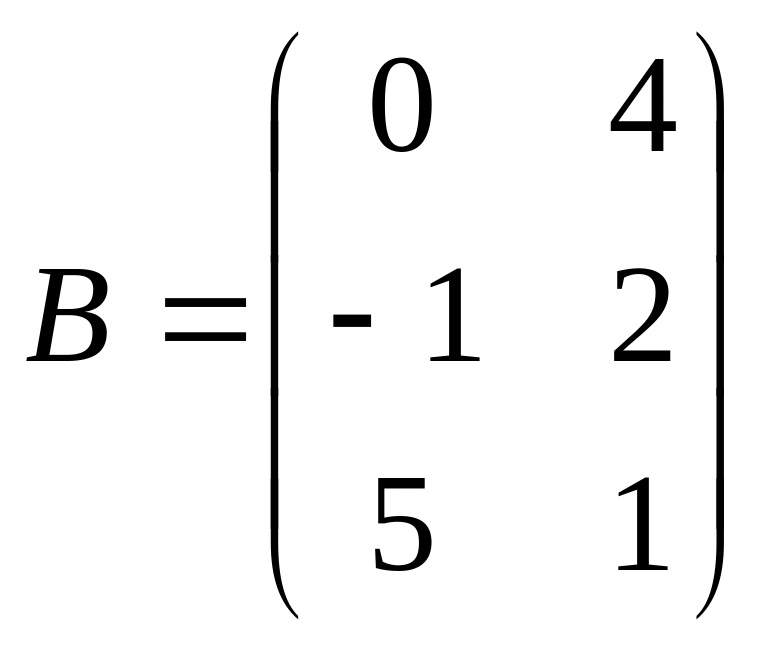 ,
,![]() .Жауабы(Отв.):
.Жауабы(Отв.):
![]() .
.
Кері матрицаларды табу керек: а) қосалқы матрицалар әдісімен, б) элементар түрлендірулер әдісімен. АА-1=Е формуласын қолданып, текеру керек. (Найти матрицы, обратные данным: а) методом присоединенной матрицы, б) методом элементарных преобразований. Сделать проверку, пользуясь формулой АА-1=Е):
а)
 ,
б)
,
б)
 .
.
Матрица рангісін анықта (Определить ранг матриц):
а)
 ,
б)
,
б)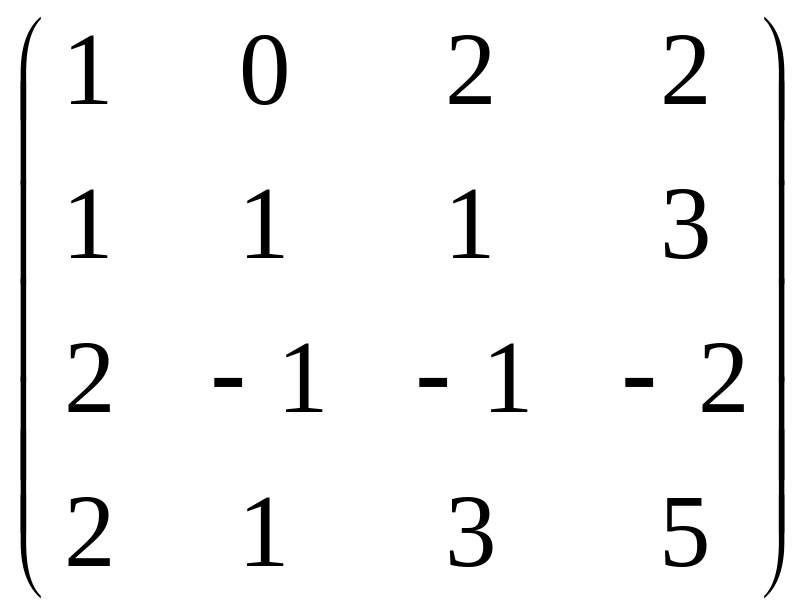 .
Жауабы (Отв.): а)r=2,
б) r=3.
.
Жауабы (Отв.): а)r=2,
б) r=3.
5. Теңдеулер жүйесін шеш: а) Крамер формуласымен; б) матрицалар әдісімен (кері матрицаны элементар түрлендірулер әдісімен тап) (Решить системы уравнений: а) по формуле Крамера; б) матричным методом (обратную матрицу найти методу элементарных преобразований)):
а)
![]() ,
б)
,
б)
![]() .
Жауабы (Отв.): а) (0,1,1), б) (1,1,-1).
.
Жауабы (Отв.): а) (0,1,1), б) (1,1,-1).
Теңдеулер жүйесін Гаусс әдісімен шеш:
а)
![]() ,
б)
,
б)
![]() .
.
Жауабы (Отв.): а) (-1,2,0,-1),
б)
![]()
![]()
![]()
![]()
![]() .
.
7. a, b, c векторлары базис құратынын дәлелде. d векторын (a, b, c) базис бойынша жікте(Доказать, что векторы a, b, c образуют базис. Разложить вектор d по базису (a, b, c): a(1,2,1), b(4,3,3), c(-2,-4,-1), d(3,1,2).
Жауабы: d=a+b-с.
Вариант 12
Анықтауыштардың дәрежесін төмендетіп есептеу керек (Вычислить определители методом понижения порядка):
а)
 б)
б) .
Жауабы(Отв.): а)12 , б)-1800 2. С=2AB+3E
матрицасын тап, егер (Найти
матрицу С=2AB+3E,
если):
.
Жауабы(Отв.): а)12 , б)-1800 2. С=2AB+3E
матрицасын тап, егер (Найти
матрицу С=2AB+3E,
если):
![]() ,
,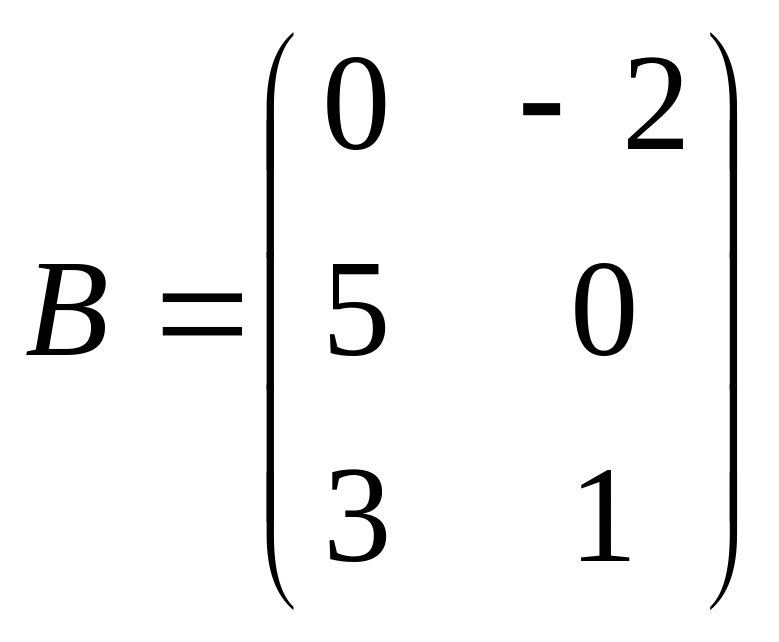 ,
.Жауабы(Отв.):
,
.Жауабы(Отв.):
![]() .
.
3.Кері матрицаларды табу керек: а) қосалқы матрицалар әдісімен, б) элементар түрлендірулер әдісімен. АА-1=Е формуласын қолданып, текеру керек. (Найти матрицы, обратные данным: а) методом присоединенной матрицы, б) методом элементарных преобразований. Сделать проверку, пользуясь формулой АА-1=Е):
а)
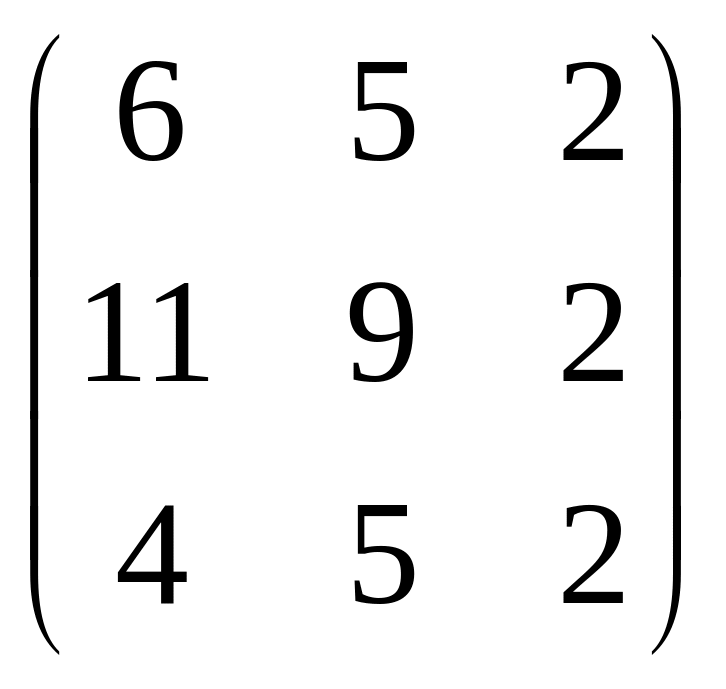 ,
б)
,
б)
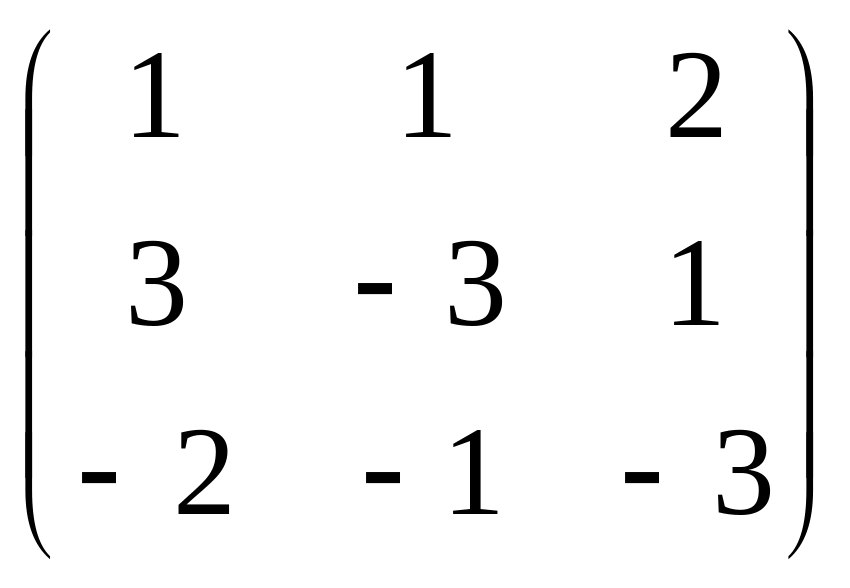 .
.
4. Матрица рангісін анықта (Определить ранг матриц):
а)
 ,
б)
,
б)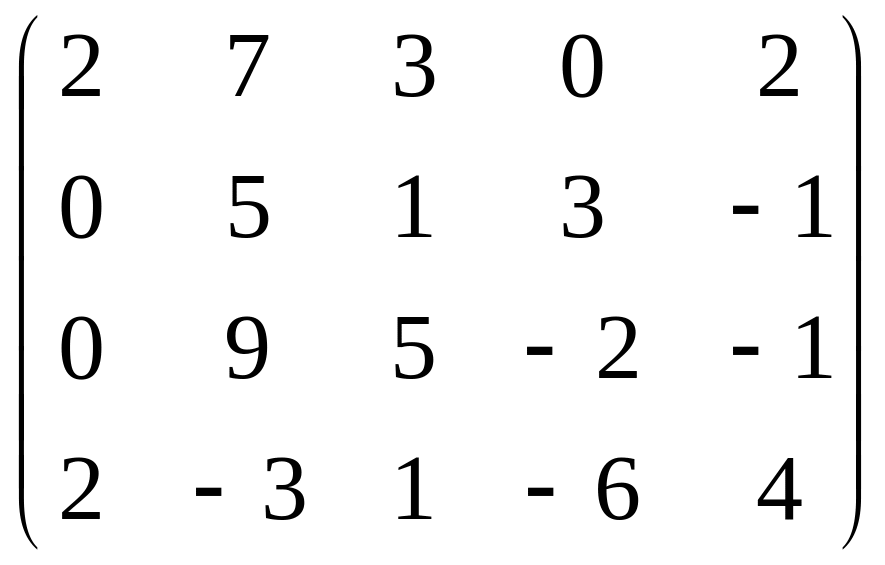 .
Жауабы (Отв.): а)r=2,
б) r=3.
.
Жауабы (Отв.): а)r=2,
б) r=3.
5. Теңдеулер жүйесін шеш: а) Крамер формуласымен; б) матрицалар әдісімен (кері матрицаны элементар түрлендірулер әдісімен тап) (Решить системы уравнений: а) по формуле Крамера; б) матричным методом (обратную матрицу найти методу элементарных преобразований)):
а)
![]() ,
б)
,
б)
![]() .
Жауабы (Отв.): а) (0,1,2 , б) (1,0:1
.
Жауабы (Отв.): а) (0,1,2 , б) (1,0:1
6. Теңдеулер жүйесін Гаусс әдісімен шеш:
а)
![]() ,
б)
,
б)
![]() .
.
Жауабы (Отв.): а) (2,1,1,0),
б)
![]()
![]()
![]() .
.
7. a, b, c векторлары базис құратынын дәлелде. d векторын (a, b, c) базис бойынша жікте(Доказать, что векторы a, b, c образуют базис. Разложить вектор d по базису (a, b, c): a(6,2,1), b(-4,1,-3), c(1,-3,-2), d(3,11,7).
Жауабы: d=a-3с.
Вариант 13
Анықтауыштардың дәрежесін төмендетіп есептеу керек (Вычислить определители методом понижения порядка):
а)
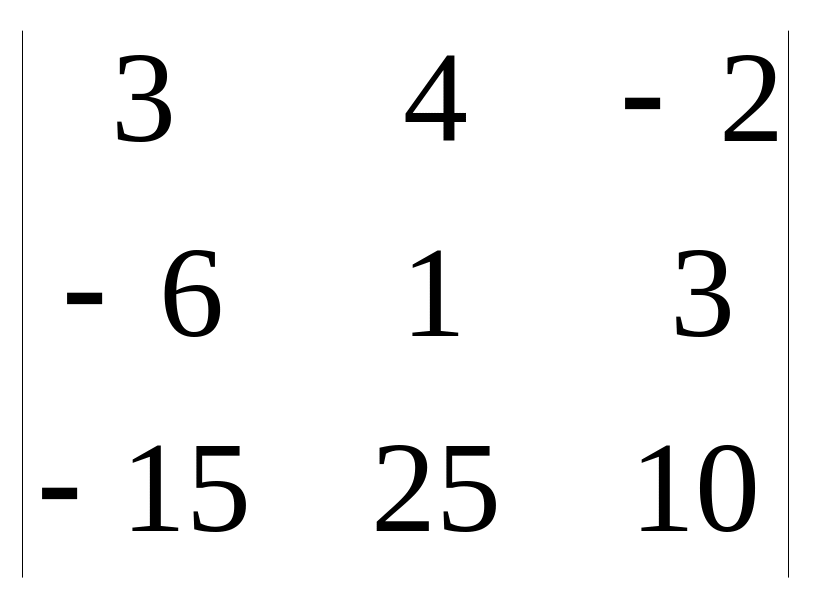 б)
б)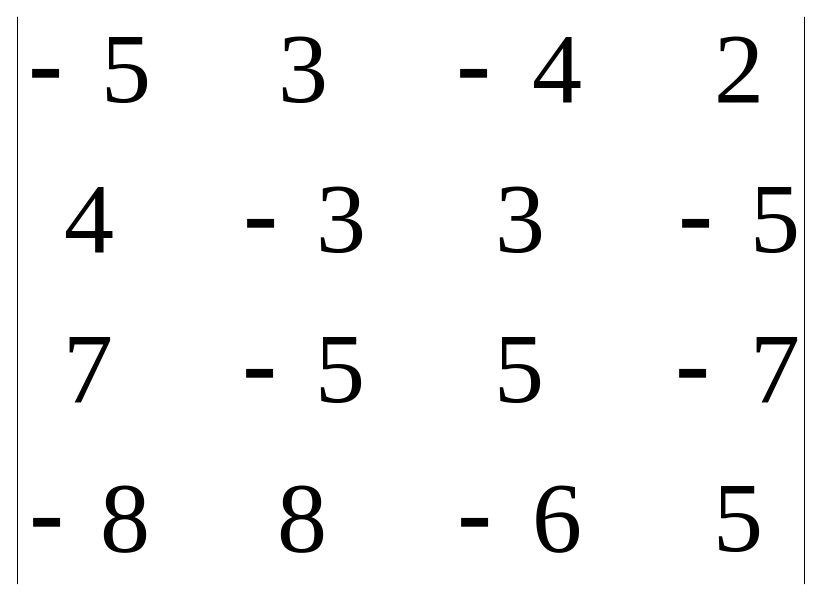 .
Жауабы(Отв.): а)135 , б) 17 2. С=2AB+3E
матрицасын тап, егер (Найти
матрицу С=2AB+3E,
если):
.
Жауабы(Отв.): а)135 , б) 17 2. С=2AB+3E
матрицасын тап, егер (Найти
матрицу С=2AB+3E,
если):
 ,
,![]() ,
, .Жауабы(Отв.):
.Жауабы(Отв.):
 .
.
3.Кері матрицаларды табу керек: а) қосалқы матрицалар әдісімен, б) элементар түрлендірулер әдісімен. АА-1=Е формуласын қолданып, текеру керек. (Найти матрицы, обратные данным: а) методом присоединенной матрицы, б) методом элементарных преобразований. Сделать проверку, пользуясь формулой АА-1=Е):
а)
 ,
б)
,
б)
 .
.
4. Матрица рангісін анықта (Определить ранг матриц):
а)
 ,
б)
,
б) .
Жауабы (Отв.): а)r=2,
б) r=3.
.
Жауабы (Отв.): а)r=2,
б) r=3.
5. Теңдеулер жүйесін шеш: а) Крамер формуласымен; б) матрицалар әдісімен (кері матрицаны элементар түрлендірулер әдісімен тап) (Решить системы уравнений: а) по формуле Крамера; б) матричным методом (обратную матрицу найти методу элементарных преобразований)):
а)
![]() ,
б)
,
б)
![]() .
Жауабы (Отв.): а) (1,-1,1 ) б)
(2,1:-2)
.
Жауабы (Отв.): а) (1,-1,1 ) б)
(2,1:-2)
6. Теңдеулер жүйесін Гаусс әдісімен шеш:
а)
![]() ,
б)
,
б)
![]() .
.
Жауабы (Отв.): а) (1,2,-1,-1)
б)
![]()
![]()
![]()
![]() .
.
7. a, b, c векторлары базис құратынын дәлелде. d векторын (a, b, c) базис бойынша жікте(Доказать, что векторы a, b, c образуют базис. Разложить вектор d по базису (a, b, c): a(1,2,1), б(5,41), c(-3,-5,1), d(7,8,3).
Жауабы: d=2a+б.
