Министерство образования и науки Украины

Национальный аэрокорсмический университет им. Н.Е. Жуковского “ХАИ”

Кафедра Проектирования радиоэлектронных систем Летательных Аппаратов

СИСТЕМЫ ПЕРЕДАЧИ ДАННЫХ

ОСНОВЫ ТЕОРИИ ПЕРЕДАЧИ ИНФОРМАЦИИ

“ОСНОВЫ ОБРАБОТКИ ИЗОБРАЖЕНИЙ”

Лабораторный практикум

Моделирование на ЭВМ

с использованием пакета MATLAB

Шульгин В.И.

Харьков 2013

Обработка изображений с использованием

MATLAB Image Processing Toolbox

Значительную часть данных, передаваемых в современных системах передачи информации, в настоящее время составляют неподвижные изображения и видео. В связи с этим, знакомство с методами представления, анализа, обработки и передачи изображений и видео, как одного из типов информации в системах передачи данных, имеет очень важное значение при изучении принципов их построения и проектирования.

Чрезвычайно удобным и гибким инструментом для решения перечисленных задач является пакет Image Processing Toolbox среды MATLAB.

Что такое Image Processing Toolbox?

Приложение Image Processing Toolbox представляет собой набор функций, которые расширяют возможности моделирования в среде MATLAB. Приложение Image Processing Toolbox поддерживает различные операции обработки изображений, включая:

• пространственные преобразования изображений

• линейную и нелинейную фильтрацию изображений

• анализ и улучшение изображений

• восстановление изображений

• сжатие (компрессию) изображений

Представление цифровых изображений.

Изображение можно представить как двумерную функцию f(x,y), где x и y – это пространственные координаты (на плоскости), а f - амплитуда (яркость, интенсивность) изображения в точке с координатами ( x, y).

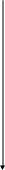
x

f(x,y)

y

Ц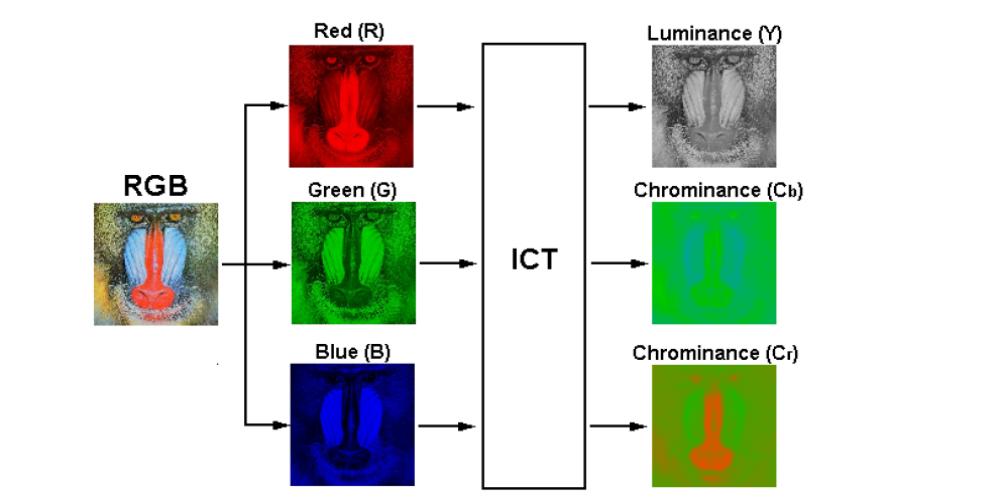 ветные изображения представляют собой комбинацию из трех монохромных изображений (компонент). В цветовой системе RGB – это красная, зеленая и синяя компоненты, в системе YUV – это яркостная и две цветоразностных компоненты.

Связь между представлениями полноцветного изображения при разных цветовых схемах можно записать в матричной форме:

Для обратного преобразования YUV в цвета RGB нужно обратить матрицу ICT и подставить ее в соответствующую матричную форму.

Естественные изображения (фотографии, кино) обычно носят непрерывный характер – координаты x, y и яркость f для них могут принимать любые значения. При передаче таких изображений по цифровым каналам связи, а также при их хранении и обработки в цифровом виде такие изображения должны подвергаться дискретизации по пространственным координатам и по уровню (дискретизации и квантованию).

При этом координаты x, y точек изображения, а также значения яркости f становятся дискретными - x_i, y_j и f ^q(x_i, y_j) .

Такое изображение называется цифровым. А значение элемента изображения называется "пиксель" - это сокращенно от "picture element".

Строка

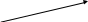
Пиксель f(x_i,y_j)

Изображения в MATLAB и Image Processing Toolbox.

Основной структурной единицей данных в MATLAB является массив. Для представления изображения данные в массиве должны нести информацию о значениях интенсивностей изображения.

MATLAB запоминает изображения в виде двумерного массива (т.е. матрицы размером M × N), в котором каждый элемент c координатами (x,y) соответствует одному пикселю изображения.

Координаты пикселей x и y могут принимать целые значения от 1 до M и от 1 до N, соответственно.

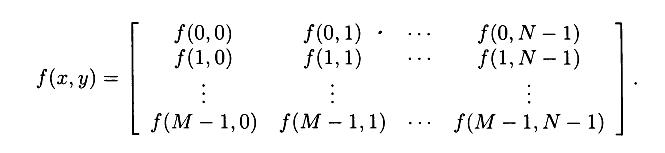
Например, если изображение состоит из 200 строк и 300 столбцов, то оно в системе MATLAB запоминается в виде матрицы с размерностью 200 × 300.

Полноцветные изображения представляются в виде трехмерных массивов (например – RGB), где имеются красная, зеленая и синяя составляющие.

Индексация массивов в MATLAB начинается с 1, поэтому соответствующая матрица в MATLAB будет иметь вид

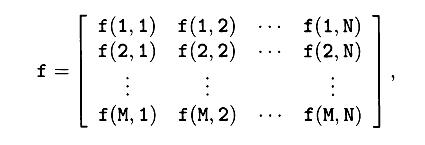
Считывание изображений.

Изображения для их обработки в MATLAB хранятся в файла, поэтому первым действием при работе с изображением является его загрузка в программу.

Очистим рабочее пространство MATLAB от всех переменных и закроем открытые окна отображений.

clear, close all

Для считывания изображений используется функция imread.

В этом примере показано считывание изображения pout.tif, которое включено в приложение Image Processing Toolbox, и его запоминание в виде массива I.

I = imread('pout.tif');

Для считывания изображения, расположенного в некоторой конкретной папке нужно в явном виде указать полный путь к этой директории, например:

f = imread('D:\Myimage\rose.jpg');

В первом примере функция imread считывает данные из графического формата TIFF (Tagged Image File Format), во втором – JPEG.

Список некоторых наиболее известных поддерживаемых форматов приведен ниже:

• BMP Windows Bitmap

• GIF Graphics Interchange Format

• HDF Hierarchical Data Format

• JPEG, JPG Joint Photographic Experts Group

• PBM Portable Bitmap

• PCX Paintbrush

• PGM Portable Graymap

• PNG Portable Network Graphics

• TIFF, TIF Tagged Image File Format

Функция imread позволяет считывать изображения из графических файлов различных форматов и с разной глубиной цвета (количество бит на пиксель в каждой цветовой компоненте). Большинство форматов использует для запоминания значений пикселей 8 бит на пиксель.

Если эти данные считываются в память, то система MATLAB запоминает их в формате uint8.

Информация об изображении.

Считав изображение полезно получить информацию о нем. В частности, очень часто нужна информация о размере изображения (количество пикселей по вертикали и по горизонтали). Сделать это можно по команде:

size(I)

Ответом программы будет:

ans = 291 240.

Типы изображений.

Пакет Image Processing Toolbox работает со следующими типами изображений:

- полутоновые изображения (изображения в градациях серого);

- двоичные (черно-белые) изображения;

- цветные изображения RGB.

Полутоновые изображения

Полутоновое изображение – это матрица, элементы которой представлены в виде числовых значений классов uint8 [0,255], или uint16 [0,65535].

Двоичные изображения

Двоичные изображения в MATLAB представляют сомой матрицу логических элементов 0 или 1. Для преобразования числовых массивов в логические служит функция logical - B=logical(A)

Полноцветные изображения

Полноцветные изображения представляют собой такой тип изображений, где каждый пиксель описывается тремя значениями красной, синей и зеленой составляющих. Система MATLAB запоминает полноцветные изображения в виде массива данных с размерностью m×n×3. В этом массиве хранится каждая компонента цвета для каждого отдельного пикселя.

Графический файловый формат запоминает полноцветные изображения как 24-битные данные, где красная, зеленая и синяя компонента представлены 8 битами каждая. В сумме это дает около 16 миллионов цветов.

Полноцветные изображения могут быть представлены в формате uint8, uint16, single или double.

Вывод изображения на дисплей.

Теперь рассмотрим вопрос отображения считанного изображения.

Изображение можно вывести на дисплей с помощью функции imshow, имеющей следующий синтаксис:

imshow(f, G)

где f – матрица изображения, G – число градаций яркости, используемых для отображения. Если параметр G не указан, то по умолчанию G = 256.

imshow(I)

Если нужно вывести на дисплей последовательно несколько изображений, сделать это можно так:

imshow(I), figure, imshow(f)

Пример:

clear, close all

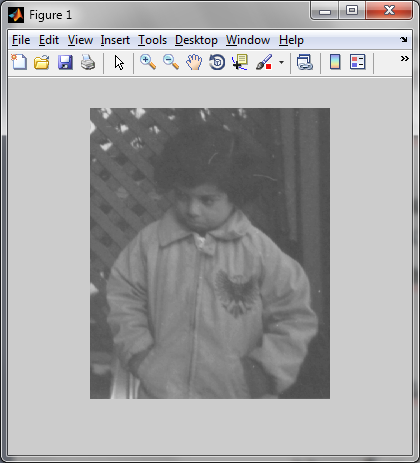
I = imread('pout.tif');

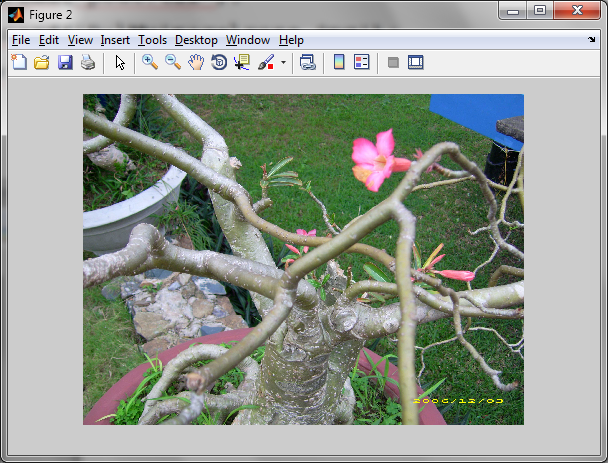
f = imread('D:\Myimage\rose.jpg');

imshow(I), figure, imshow(f)

Результат:

Фильтрация и подавление шумов на изображении.

Одной из наиболее часто решаемых задач обработки изображений является фильтрация или подавление шумов на изображении.

При моделировании задач фильтрации в MATLAB возникает необходимость генерирования моделей различных по характеру шумов и зашумления изображений.

Поскольку изображения, представляют собой двумерные функции, соответственно и шумы на изображении также имеют двумерный характер.

Для зашумления изображений служит команда imnoise, имеющая следующий синтаксис:

J = imnoise(I,type)

J = imnoise(I,type,parameters)

Где строковая переменная type может принимать одно из значений:

• 'gaussian' - для гауссового белого шума;

• 'localvar' - для гауссового белого шума с нулевым математическим ожиданием и локальной мощностью, зависящей от яркости текущего участка изображения;

• 'poisson' – пуассоновский шум;

• 'salt & pepper' – для шума в виде черных и белых пикселов (шум называется - «соль и перец»);

Кроме этого J = imnoise(I,type,parameters) – дополнительно задаются параметры соответствующего типа шума.

Например:

J = imnoise(I,'gaussian',m,v) – добавление к изображению I гауссового БШ со средним m и дисперсией v. По умолчанию m=0, v=0.01.

J = imnoise(I,'poisson') – генерирует пуассоновский шум из данных, вместо того чтобы добавлять к данным искусственный шум.

J = imnoise(I,'salt & pepper',d), где параметр d - плотность шума. В результате генерируется примерно d*prod(size(I)) пикселей шума. По умолчанию d=0.05.

Изображение I может принадлежать классу uint8 или uint16. Результирующее изображение J принадлежит тому же классу, что и I, и имеет тот же размер.

Пример 1:

clear;

close all;

I = imread('eight.tif');

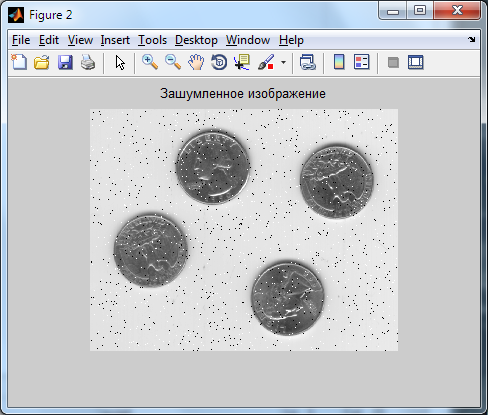
J = imnoise(I,'salt & pepper',0.02);

Imshow(I)

title('Исходное изображение');

figure, imshow(J)

title('Зашумленное изображение');

Р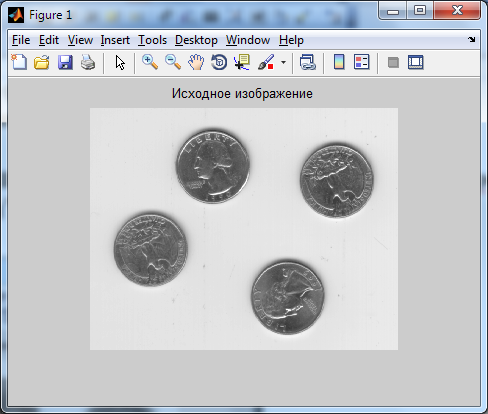 езультат операции добавления шума типа 'salt & pepper' к изображению – его “зашумления” показан ниже:

Пример 2:

I = imread('eight.tif');

J = imnoise(I,'gaussian');

Imshow(I)

title('Исходное изображение');

figure, imshow(J)

title('Зашумленное изображение');

В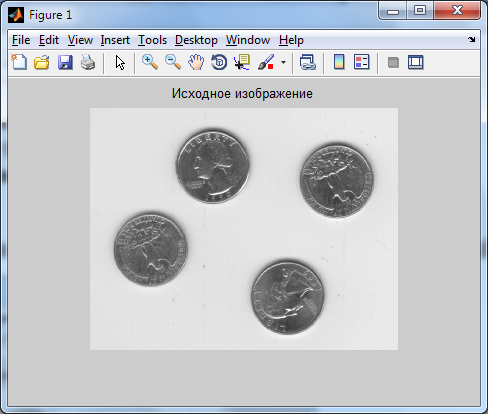 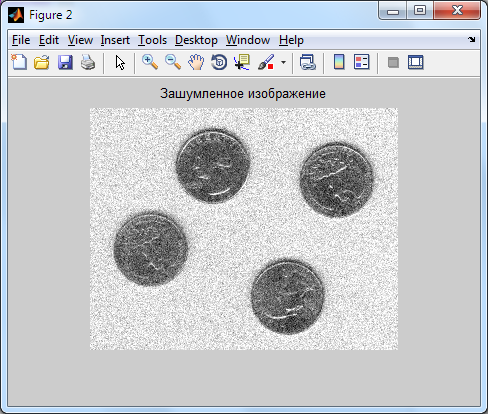этом примере в качестве шума использован нормальный (гауссов) белый шум

Методы фильтрации изображений.

Ослабление действия помех достигается фильтрацией. При фильтрации яркость каждой точки исходного изображения, искаженного помехой, заменяется некоторым другим значением яркости, которое полагается в меньшей степени искаженным помехой.

Что может послужить основой для различения сигналов и помех на изображении? Изображение представляет собой двумерную функцию пространственных координат, которая обычно изменяется по этим координатам медленнее (иногда значительно медленнее), чем помеха. Это позволяет при оценке полезного сигнала в каждой точке кадра принять во внимание подобие множества соседних точек полезного изображения, то есть воспользоваться определенной похожестью сигнала в этих точках.

В других случаях, наоборот, признаком полезного сигнала являются резкие перепады – границы яркости. И в этом случае свойства сигнала проявляются при наблюдении его не только в локальной точке, но и с учетом поведения изображения в окрестностях этой точки.

Таким образом, идеология фильтрации основывается на рациональном использовании данных, как фильтруемой точки, так и ее окрестности.

Линейная фильтрация

Для пояснения процедуры линейной фильтрации изображения сначала рассмотрим процесс линейной дискретной фильтрации одномерных данных – сигналов.

Пусть (x₁, x₂, x₃, x₄, … x_i … x_n-1, x_n) – дискретная последовательность на входе линейного фильтра, (y₁, y₂, y₃, y₄, … y_i, … y_n-1, y_n) - последовательность на выходе фильтра, и (h₀, h₁, …. , h_m) – импульсная переходная характеристика фильтра.

x_i

y_i

h_k

Тогда сигнал на выходе фильтра y_i при подаче на его вход сигнала x_i

определяется следующим образом:

y_i =

Эта формула – известное вам выражение для линейной дискретной свертки, дискретный аналог интеграла Дюамеля, описывающего соотношение между входом и выходом любого линейного звена.

Если раскрыть сумму в этом выражении, получим:

y_i = x_i h₀ + x_i-1 h₁ + x_i-2 h₂ + x_i-3 h₃ + …

Это выражение можно объяснить так. Сигнал на выходе фильтра в i-тый момент есть сигнал на его входе в этот же момент, умноженный на h_0, плюс сигнал на входе в предшествующий момент времени i-1, умноженный на h₁ плюс сигнал на входе в момент времени i-2, умноженный на h₂ и так далее. Иными словами, текущее значение сигнала на выходе фильтра представляет собой сумму входных значений с весами, зависящими от вида ИПХ фильтра. Можно дать еще одну интерпретацию работы фильтра – линейный фильтр на своем выходе усредняет значения входного сигнала с весами, определяемыми видом ИПХ этого фильтра.

Аналогичным образом выполняется фильтрация двумерных дискретных сигналов – изображений. Отличие состоит в том, что входной сигнал фильтра, выходной сигнал фильтра и ИПХ представляют собой двумерные функции x_ij , y_ij и h_kl соответственно, и дискретная свертка также имеет двумерный характер

y_ij =

То есть, точка изображения на выходе двумерного линейного фильтра представляет собой сумму (среднее значение) всех соседних точек фильтруемого изображения, взятых с весами, определяемыми видом ИПХ фильтра.

Такая процедура еще называется оконной фильтрацией, где окно фильтра – это его ИПХ. Все элементы фильтруемого изображения, попавшие в окно – усредняются и тем самым формируют выходной сигнал фильтра.

Процедура же фильтрации для всего изображения – это последовательное выполнение фильтрации каждой точки. То есть, окно фильтра "пробегает" по всем элементам фильтруемого изображения и в каждом своем положении формирует усредненное значение яркости по всем точкам, попавшим в окно.

Окно фильтра

Процедура линейной фильтрации изображения в MATLAB выполняется с использованием команды