1. Образование пузырей в жидкости

1.1. Образование пузырей при продувке жидкости

Продувка жидкой ванны газом в металлургии играет очень важную роль, причем в зависимости от конкретных условий ее осуществляют сверху, снизу и сбоку ванны, через специальные фурмы, перфорированное днище и т.д. Представим себе, что через перфорированный лист в жидкость подается газ (рис. 1). При небольших расходах газа истечение происходит в виде отдельных пузырей, образованию которых препятствуют силы поверхностного натяжения.

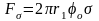(1.1)

и силы гидравлического сопротивления

(1.2)

или в случае вязкой среды (закон Стокса)

,

где r₁ и r – радиусы отверстия и пузыря; _о – коэффициент сужения шейки 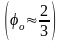; С_х – коэффициент гидравлического сопротивления; _с – динамический коэффициент вязкости сплошной среды (жидкости); _с –плотность дисперсной среды (газа); w – относительная скорость перемещения границы раздела фаз, которую можно представить в виде

. (1.3)

Скорость роста пузыря w можно связать со скоростью истечения газа через отверстие w₁, используя уравнение сплошности в виде

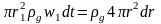(1.4)

Откуда

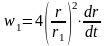. (1.5)

Скорость роста пузыря не является величиной постоянной и изменяется во времени по закону

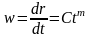, (1.6)

причем характер представленной зависимости определяется условиями истечения.

Время формирования пузыря t₁ можно определить из закона сохранения массы

или

, (1.7)

где r_о – радиус пузыря в момент отрыва; – средняя скорость газа за время t₁.

Время между двумя последовательными отрывами пузырей t₂ может быть больше t₁, тогда средняя скорость газа в отверстиях перфорированного листа

.

Эта величина связана с перепадом давления, под действием которого происходит истечение газа в жидкость, т.е.

, (1.8)

где  – коэффициент скорости.

Если t=t₁, то пузыри непрерывно следуют один за другим, под перфорированным листом образуется газовая подушка. Для случая m=0 и t₂=0 величина минимальной скорости газа в отверстиях, при которой имеет место непрерывное истечение пузырей:

, (1.9)

где _с – плотность сплошной среды.

Момент отрыва пузыря характеризуется равновесием сил поверхностного натяжения F_, сил гидравлического сопротивления F_S и архимедовой силы

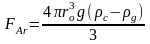, (1.10)

где r_о – радиус пузыря в момент отрыва.

При приближенном анализе обычно пренебрегают гидравлическим сопротивлением среды из равенства архимедовой силы и сил поверхностного натяжения

. (1.11)

При истечении в вязкую среду равенство сил действующих на пузырь в момент отрыва

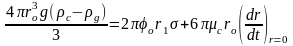(1.12)

Подставляя в формулу (1.12) соотношение (1.5), записанное в виде

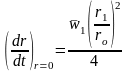, (1.13)

получим

. (1.14)

Сопоставляя формулы (1.11) и (1.14) видно, что при увеличении вязкости жидкости отрывной радиус пузыря возрастает.

Истечение при квадратичном законе сопротивления имеет место при истечении в жидкость газовых пузырей достаточно большого размера. Аналогично формуле (12) можно записать

. (1.15)

Используя соотношения (1.8), (1.13) и (1.15), получим

. (1.16)

Сопоставление формул (1.11) и (1.16) показало, что при прочих равных условиях, отрывной радиус пузыря возрастает с уменьшением плотности барботирующего газа и увеличением перепада давления, под действием которого происходит истечение.