ББК 32.973.2-018я73

М 48-2

Мельникова О. И., Бархатова И. А., Беднякова Т.М., Васильев В.А., Павлов А.С., Флорко А. Б.

М 48-2 Сборник задач по программированию. Учебное пособие.— Дубна: Международный университет природы, общества и человека «Дубна», 2011.— с.: ил.

ISBN 5—89847—035—2

Учебное пособие содержит задачи, необходимые для освоения базовых приемов программирования. Задачи разделены по темам, начальные главы содержат примеры решения наиболее типичных задач. Задачи, содержащиеся в дополнительной главе, позволят оценить уровень освоения курса.

Пособие предназначено для студентов 1 курса Международного университета природы, общества и человека «Дубна», изучающих дисциплины «Программирование на языке высокого уровня» и «Практикум на ЭВМ», а также для всех желающих освоить приемы современного программирования.

Рецензенты:

Международный университет природы, общества и человека «Дубна»

141980 Г.Дубна Московской обл., ул.Университетская, 19

 Авторы. 2011

ISBN 5—89847—035—2  Международный университет природы,

общества и человека «Дубна», 2011

Оглавление

Введение 3

1. Условные выражения 4

2. Циклы 13

3. Массивы 18

3.1. Заполнение одномерного массива 19

3.2 Двумерные массивы 26

4. Строки 42

5. Классы 51

6. Графика 59

7. Файлы 67

8. Дополнительные задачи 71

Введение

1. Условные выражения

Пример: Дано целое число A. Проверить истинность высказывания: «Число A является четным».
int A; A = Convert.ToInt32(Console.ReadLine()); if (A % 2 == 0) Console.WriteLine("true"); else Console.WriteLine("false");	Объявляем целочисленную переменную A Присваиваем A значение, которое вводится пользователем с клавиатуры. При этом не забываем конвертировать вводимое число в целочисленный тип данных. Проверяем делится ли наше число на два без остатка. Если делится – выводим true. В противном случае выводим false.

1. Дано целое число A. Проверить истинность высказывания: «Число A является положительным».

2. Определить, является ли число введенное пользователем отрицательным.

3. Определить знак числа, введенного пользователем.

4. Дано целое число A. Проверить истинность высказывания: «Число A является нечетным». Определить, является ли число введенное пользователем нечетным.

5. Дано целое число A. Проверить истинность высказывания: «Число A является четным».

6. Даны два целых числа: A, B. Проверить истинность высказывания: «A кратно B».

7. Даны два действительных числа x, y. Получить: max(x, y); min(x, y).

Пример: Даны два целых числа: A, B. Проверить истинность высказывания: «Справедливы неравенства A > 2 и B ≤ 3».

int A, B; A = Convert.ToInt32(Console.ReadLine()); B = Convert.ToInt32(Console.ReadLine()); if (A > 2 && B <= 3) Console.WriteLine("true"); else Console.WriteLine("false");

Объявляем целочисленные переменные A и B. Присваиваем A значение, которое вводится пользователем с клавиатуры. При этом не забываем конвертировать вводимое число в целочисленный тип данных. Аналогичное делаем для B. В решении этой задачи необходим логический оператор! Поскольку мы должны проверить действительно ли A > 2 и при этом B ≤ 3 одновременно. Если это верно – выводим true. В противном случае выводим false.

8. Даны два целых числа: A, B. Проверить истинность высказывания: «Справедливы неравенства A ≥ 0 или B < –2».

9. Даны три целых числа: A, B, C. Проверить истинность высказывания: «Справедливо двойное неравенство A < B < C».

10. Даны три действительных числа. Выбрать из них те, которые принадлежат интервалу (2, 8).

11. Даны действительные числа x1,…, x10. Вычислить f(a) для каждого числа xi, если

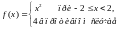
12. Даны действительные числа x1,…, x13. Вычислить f(a) для каждого числа xi, если

13. Даны действительные числа x, y (x не равно y). Меньшее из этих двух чисел заменить их полусуммой, а большее - их удвоенным произведением.

14. A) Найти наибольшее из трех чисел, введенных пользователем.

Б) Найти наименьшее из трех чисел, введенных пользователем.

В) Найти наибольше и наименьшее из трех чисел, введенных пользователем.В

15. Даны три целых числа: A, B, C. Проверить истинность высказывания: «Число B находится между числами A и C».

16. Даны два целых числа: A, B. Проверить истинность высказывания: «Каждое из чисел A и B нечетное».

17. Даны два целых числа: A, B. Проверить истинность высказывания: «Хотя бы одно из чисел A и B нечетное».

18. Даны два целых числа: A, B. Проверить истинность высказывания: «Только одно из чисел A и B нечетное».

19. Даны два целых числа: A, B. Проверить истинность высказывания: «Числа A и B имеют одинаковую четность».

Для решения данной задачи существует два решения, одно из которых очевидно:

if (A%2==1 && B%2==1) || (A%2== && B%2 ==0)

Однако в задаче спрашивается только про одинаковую четность значений A и B, т.е. необходимо проверить равенство

(A%2 == B%2)

20. Даны три целых числа: A, B, C. Проверить истинность высказывания: «Каждое из чисел A, B, C положительное».

21. Даны три целых числа: A, B, C. Проверить истинность высказывания: «Хотя бы одно из чисел A, B, C положительное».

22. Даны три целых числа: A, B, C. Проверить истинность высказывания: «Ровно одно из чисел A, B, C положительное».

Алгоритм решения:

Добавим переменную p = 0, которая будет посчитывать количество положительных чисел

Проверяем условия:

If (A > 0) p++;

If (B > 0) p++;

If (C > 0) p++;

// Осталось проверить значение р

If (p == 1) вывод результата на экран!!!

23. Даны три целых числа: A, B, C. Проверить истинность высказывания: «Ровно два из чисел A, B, C являются положительными».

24. Дано целое положительное число. Проверить истинность высказывания: «Данное число является четным двузначным».

25. Дано целое положительное число. Проверить истинность высказывания: «Данное число является нечетным трехзначным».

26. Проверить истинность высказывания: «Среди трех данных целых чисел есть хотя бы одна пара совпадающих (равных)».

27. Проверить истинность высказывания: «Среди трех данных целых чисел есть хотя бы одна пара взаимно противоположных».

28. Дано трехзначное число. Проверить истинность высказывания: «Все цифры данного числа различны».

29. Дано трехзначное число. Проверить истинность высказывания: «Цифры данного числа образуют возрастающую последовательность».

30. Дано трехзначное число. Проверить истинность высказывания: «Цифры данного числа образуют возрастающую или убывающую последовательность».

31. Дано четырехзначное число. Проверить истинность высказывания: «Данное число читается одинаково слева направо и справа налево».

32. Даны числа A, B, C (число A не равно 0). Рассмотрев дискриминант D = B² – 4·A·C, проверить истинность высказывания: «Квадратное уравнение A·x² + B·x + C = 0 имеет вещественные корни».

33. Определить количество корней квадратного уравнения, коэффициенты вводятся пользователем.

34. Даны числа x, y. Проверить истинность высказывания: «Точка с координатами (x, y) лежит во второй координатной четверти».

35. Даны числа x, y. Проверить истинность высказывания: «Точка с координатами (x, y) лежит в четвертой координатной четверти».

36. Даны числа x, y. Проверить истинность высказывания: «Точка с координатами (x, y) лежит во второй или третьей координатной четверти».

37. Даны числа x, y. Проверить истинность высказывания: «Точка с координатами (x, y) лежит в первой или третьей координатной четверти».

38. Определить в какой координатной плоскости лежит точка, координаты которой вводит пользователь.

39. Даны числа x, y, x₁, y₁, x₂, y₂. Проверить истинность высказывания: «Точка с координатами (x, y) лежит внутри прямоугольника, левая верхняя вершина которого имеет координаты (x₁, y₁), правая нижняя — (x₂, y₂), а стороны параллельны координатным осям».

40. Даны целые числа a, b, c, являющиеся сторонами некоторого треугольника. Проверить истинность высказывания: «Треугольник со сторонами a, b, c является равносторонним».

41. Даны целые числа a, b, c, являющиеся сторонами некоторого треугольника. Проверить истинность высказывания: «Треугольник со сторонами a, b, c является равнобедренным».

42. Даны целые числа a, b, c, являющиеся сторонами некоторого треугольника. Проверить истинность высказывания: «Треугольник со сторонами a, b, c является прямоугольным».

43. Даны целые числа a, b, c. Проверить истинность высказывания: «Существует треугольник со сторонами a, b, c». Определить, существует ли треугольник, длины сторон которого a, b, c, где a, b, c вводит пользователь..

2. Циклы

Алгоритм решения задачи «нахождение суммы ряда»:

Пример: Дано целое число N (> 1) и две вещественные точки на числовой оси: A, B (A < B). Отрезок [A, B] разбит на N равных отрезков. Вывести H — длину каждого отрезка, а также набор точек A, A + H, A + 2·H, A + 3·H, …, B, образующий разбиение отрезка [A, B].

int N = Convert.ToInt32(Console.ReadLine()); double A = Convert.ToDouble(Console.ReadLine()); double B = Convert.ToDouble(Console.ReadLine()); double H = B - A; Console.WriteLine(H); for (int i = 0; i < N; i++) { Console.WriteLine(A + (H * i)); } В таблице 1 подробно рассмотрены значения, которые (должны) будут получать переменные

Заводим целочисленную переменную N. Помещаем в N значение, вводимое с клавиатуры, не забыв конвертировать его в целочисленный тип данных. Аналогичное делаем для A, только тип данных с плавающей точкой. Так же для B. Заводим переменную H и присваиваем ей значение (B-A) – расстояние между точками на оси. Выводим H. Идем циклом от 0 до N-1. { На каждом шагу выводим значение (A+(H*i), которое и является искомым. } i H*i A+H*i 0 0 A 1 H A+H 2 2*H A+2*H … … … N-1 (N-1)*H A+(N-1)*H N N*H A+N*H

1. Найти площадь "снеговика", если каждый новый круг увеличивается на 4.

2. Дано натуральное число n. Вычислить:

1. n!;

2. (1+1/1^2)(1+1/2^2).....(1+1/n^2);

3. 1/sin(1) + 1/(sin(1)+sin(2)) + ...... + 1/(sin(1)+...+sin(n)).

1. Даны действительное число a и натуральное число n. Вычислить:

1. a(a+1)...(a+n-1)4;

2. 1/a + 1/a(a+1) + .... + 1/a(a+1)...(a+n);

3. 1/a + 1/a^2 + 1/a^4 + ..... + 1/a^2n.

1. Дано натуральное число n. Получить последовательность b₁, …, b_n, где при i=1,2…, n значение b_i равно:

1. i;

2. i2;

3. 2i+1.

5. Даны натуральные числа n, a₁, …, a_n. Определить произведение членов a_k последовательности a₁, …, a_n, кратных 3.

6. Даны натуральные числа n, a₁, …, a_n. Определить сумму членов a_k последовательности a₁, …, a_n, не кратных 5.