5. 51. Над майданом, на висоті 5 метрів, висить точкове джерело світла. Площа поверхні всередині якої освітленість майдану не менша 1 лк, дорівнює 235,5 м2. Знайти силу джерела світла.

Рис. 5.51

Р

Дано:

= 5 м = 235,5 м2 = 1 лк

= ?

озв’язок.

Вважаємо, що поверхня, освітленість якої буде відповідати умові задачі дорівнює площі, яка обмежена колом з діаметром .

Освітленість, яка створюється точковим ізотропним джерелом силою світла , що знаходиться на відстані від точки дорівнює

, (1)

де - кут падіння променів на майдан; - відстань від джерела світла до краю столу; .

Тоді отримаємо

. (2)

У рівняння (2) підставляємо задані в умові задачі величини і отримуємо відповідь:

=

5. 52. Над майданом висить точкове джерело світла силою 200 кд. Площа поверхні, всередині якої освітленість майдану не менша 1 лк, дорівнює 235,5 м2. Знайти висоту на якій висить джерело світла.

Рис. 5.52

Р

Дано:

= 200 кд = 235,5 м2 = 1 лк

= ?

озв’язок.

Вважаємо, що поверхня, освітленість якої буде відповідати умові задачі дорівнює площі, яка обмежена колом з діаметром .

Освітленість, яка створюється точковим ізотропним джерелом силою світла , що знаходиться на відстані від точки дорівнює

, (1)

де - кут падіння променів на поверхню майдану; - відстань від джерела світла до краю столу; .

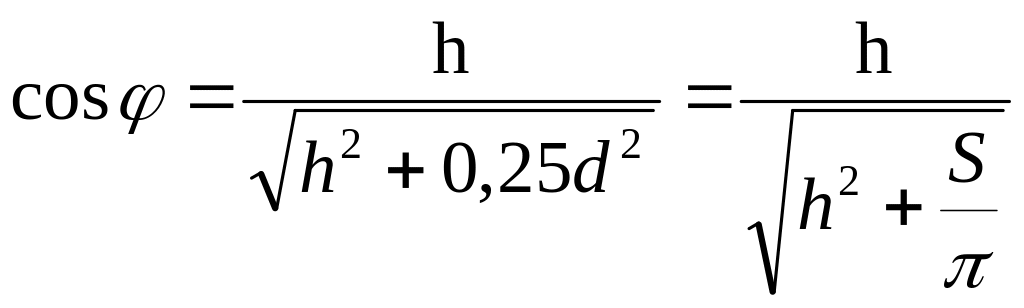Тоді отримаємо

. (2)

У рівняння (2) підставляємо задані в умові задачі величини і отримуємо відповідь:

=

5. 53. На висоті 2 метра над центром півсфери радіусом 200 см, висить точкове джерело світла силою 172 кд. Знайти освітленість в точці поверхні півсфери, на яку промені падають під кутом 30°.

Рис. 5.53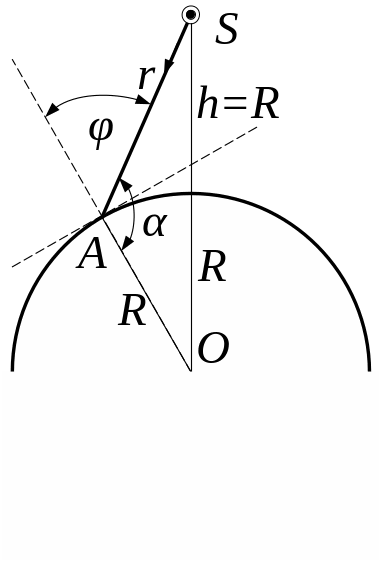

Р

Дано:

= 2 м = 200 см = 172 кд = 300

= ?

озв’язок.

Освітленість, яка створюється точковим ізотропним джерелом силою світла , що знаходиться на відстані від точки дорівнює

, (1)

де - кут падіння променів на поверхню півсфери; - відстань від джерела світла до точки на поверхні сфери, яку визначаємо з трикутника за допомогою теореми косинусів:

, (2)

Тоді з квадратного рівняння (2) отримаємо

. (3)

Остаточний результат має вигляд:

, (4)

У рівняння (4) підставляємо задані в умові задачі величини і отримуємо відповідь:

=

5. 54. На висоті 2 метра над центром півсфери, радіусом 200 см, висить точкове джерело світла силою 700 кд. Знайти освітленість в точці поверхні півсфери, на яку промені падають під кутом 42°.

Рис. 5.54

Р

Дано:

= 2 м = 200 см = 700 кд = 420

= ?

озв’язок.

Освітленість, яка створюється точковим ізотропним джерелом силою світла , що знаходиться на відстані від точки дорівнює

, (1)

де - кут падіння променів на поверхню півсфери; - відстань від джерела світла до точки на поверхні сфери, яку визначаємо з трикутника за допомогою теореми косинусів:

, (2)

Тоді з квадратного рівняння (2) отримаємо

. (3)

Остаточний результат має вигляд:

, (4)

У рівняння (4) підставляємо задані в умові задачі величини і отримуємо відповідь:

=

5. 55. На висоті 2 метра над центром півсфери, радіусом 200 см, висить точкове джерело світла силою 172 кд. Знайти освітленість в точці поверхні півсфери, на яку промені падають під кутом 0°.

Рис. 5.55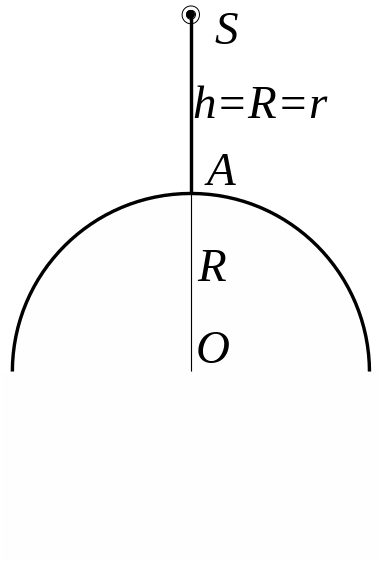

Р

Дано:

= 2 м = 200 см = 700 кд = 420

= ?

озв’язок.

Освітленість, яка створюється точковим ізотропним джерелом силою світла , що знаходиться на відстані від точки дорівнює

, (1)

де - кут падіння променів на поверхню півсфери; - відстань від джерела світла до точки .

У рівняння (1) підставляємо задані в умові задачі величини і отримуємо відповідь:

=

5. 56. Три однакові лампи вуличного освітлення з силою світла 219,7 кд, знаходяться на висоті 500 см. Відстань між лампами 12 метрів. Знайти освітленість землі в точці під середньою лампою.

Рис. 5.56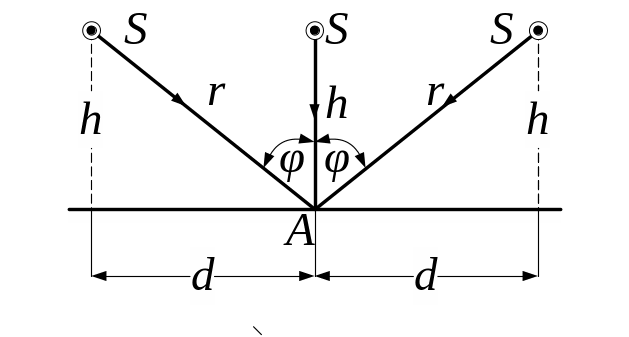

Р

Дано:

= 219,7 кд = 500 см = 12 м

= ?

озв’язок.

Освітленість, яка створюється точковим ізотропним джерелом силою світла , що знаходиться на відстані від точки дорівнює

, (1)

де - кут падіння променів на землю, у двох випадках , а в одному випадку = 0; - відстань від джерела світла до точки , у двох випадках , а в одному випадку = .

Тоді освітленість у точці дорівнюватиме

. (2)

У рівняння (2) підставляємо задані в умові задачі величини і отримуємо відповідь:

=