5. 26. На якій відстані від опуклого дзеркала потрібно помістити джерело світла, щоб його зображення вийшло на відстані 60 см від дзеркала? Фокус дзеркала дорівнює 90 см.
Розв’язок.
Ф
Дано:
= 60 см
= 90 см
= ?
Рис. 5.25
, (1)
де і - відповідно відстані предмета і зображення від полюса дзеркала; - фокусна відстань дзеркала; - радіус кривизни дзеркала. Для опуклого дзеркала і від’ємні.
А лінійне збільшення сферичного дзеркала дорівнює
, (2)
де і - лінійні розміри зображення та предмета.
З рівняння (1) отримуємо:
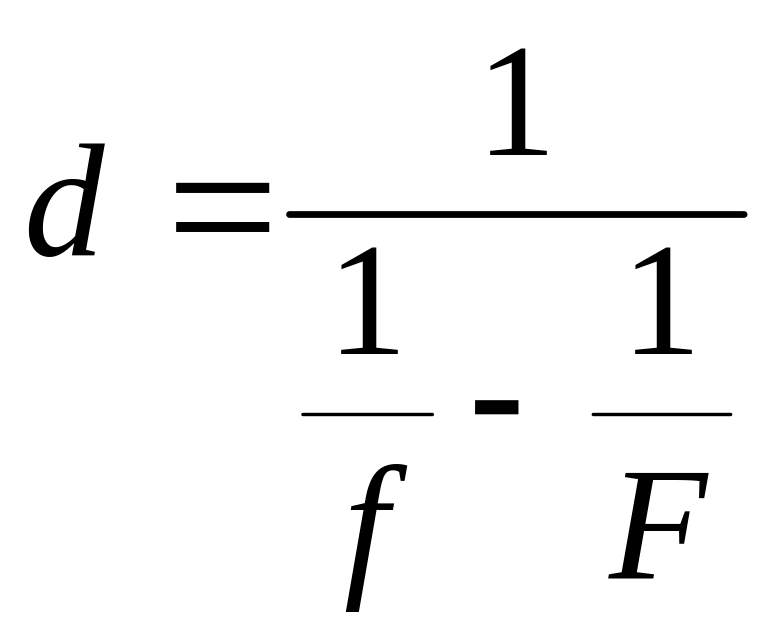(3)
Підставляємо данні умови задачі в вираз (3) і отримуємо відповідь:
= см
5. 27. На відстані 15 см від двоопуклої лінзи, оптична сила якої 10 дптр, поставлений перпендикулярно до оптичної осі предмет, висотою 2 см. Знайти висоту зображення.
Розв’язок.
Ф
Дано:
= 15 см
= 10
дптр
= 2 см
= ?
Рис. 5.27
, (1)
де і - відповідно відстані від оптичного центра лінзи до предмета і зображення; - відносний показник заломлення матеріалу лінзи; - фокусна відстань лінзи; - оптична сила лінзи. А лінійне збільшення лінзи дорівнює
, (2)
де і - лінійні розміри зображення та предмета.
Тоді з рівнянь (1) і (2) отримуємо
. (3)
У рівняння (3) підставляємо задані в умові задачі величини і отримуємо відповідь:
=
5. 28. Відстань між двома джерелами світла 24 см. На якій відстані від джерел треба поставити збірну лінзу, з фокусною відстанню 9 см, щоб зображення обох джерел світла знаходились від лінзи на одній відстані?
Розв’язок.
Ф
Дано:
= 24 см
= 9 см
= ?
Рис.5.28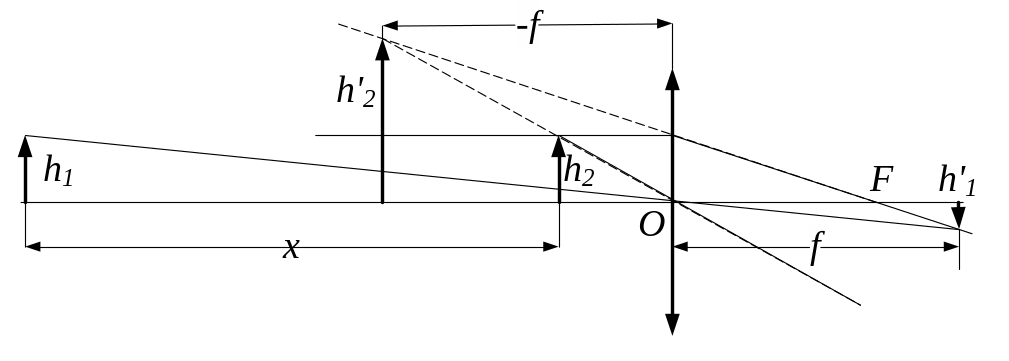
де і - відповідно відстані від оптичного центра лінзи до предмета і зображення; - відносний показник заломлення матеріалу лінзи; - фокусна відстань лінзи; - оптична сила лінзи. А лінійне збільшення лінзи дорівнює
, (2)
де і - лінійні розміри зображення та предмета.
Тоді з рівняння (1), враховуючи, що одне з зображень повинно бути уявним, отримуємо
. (3)
У квадратного рівняння (3) отримуємо відповідь:
=
5. 29. На якій відстані від лінзи з фокусною відстанню 12 см потрібно поставити предмет, щоб його дійсне зображення було втроє більше самого предмета?
Розв’язок.
Ф
Дано:
= 12 см
= 3
= ?
Рис. 5.27
, (1)
де і - відповідно відстані від оптичного центра лінзи до предмета і зображення; - відносний показник заломлення матеріалу лінзи; - фокусна відстань лінзи; - оптична сила лінзи. А лінійне збільшення лінзи дорівнює
, (2)
де і - лінійні розміри зображення та предмета.
Тоді з рівнянь (1) і (2) отримуємо
. (3)
У рівняння (3) підставляємо задані в умові задачі величини і отримуємо відповідь:
=
5. 30. При фотозйомці автомобіля, довжиною 4 м, плівка знаходилась на відстані 60 мм від об'єктива. З якої відстані фотографували автомобіль, якщо довжина його негатива 32 мм?.
Розв’язок.
Ф
Дано:
= 60 мм
= ?
Рис. 5.27
= 4 м
= 32 мм
, (1)
де і - відповідно відстані від оптичного центра лінзи до предмета і зображення; - відносний показник заломлення матеріалу лінзи; - фокусна відстань лінзи; - оптична сила лінзи. А лінійне збільшення лінзи дорівнює
, (2)
де і та і - лінійні розміри зображення та предмета.
Тоді з рівняння (2) отримуємо
. (3)
У рівняння (3) підставляємо задані в умові задачі величини і отримуємо відповідь:
=
5.
31. На стіл діаметром 2 м падає під кутом
30° до горизонталі потік
світла в 600 лм. Яка освітленість столу?
= 3.
Розв’язок.
О
Дано:
= 2 м
= 300
= 600
лм
= ?
, (1)
де
кут між променями і нормаллю до поверхні.
У рівняння (1) підставляємо задані в умові задачі величини і отримуємо відповідь:
=
5. 32. Світло від лампочки, з силою світла у 200 кд, падає під кутом 45° на робоче місце, створюючи освітленість у 140 лк. На якій відстані від робочого місця знаходиться лампочка? На якій висоті від
робочого
місця вона висить? Прийняти
= 1,4.
Р
Дано:
= 140
лк
= 450
= 200
кд
= ?,
= ?
О
Рис. 5.32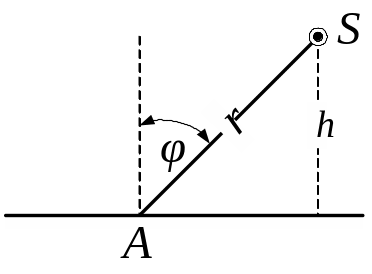
, (1)
де - кут падіння променів.
Звідки отримуємо
. (2)
З прямокутного трикутника катет дорівнює
. (3)
У рівняння (2) та (3) підставляємо задані в умові задачі величини і отримуємо відповідь:
= =
5. 33. Ліхтар із силою світла в 500 кд висить на стовпі на висоті 3 м від поверхні землі. Знайти освітленість землі в точці на відстані 4 м від підстави стовпа.
Р
Дано:
= 500
кд
= 3 м
= ?
= 4
м
О
Рис. 5.33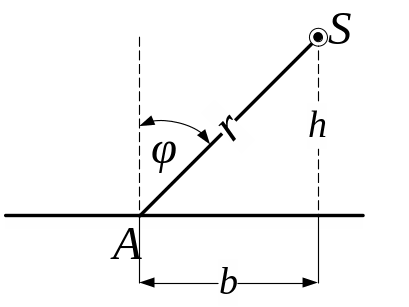
, (1)
де - кут падіння променів.
Звідки отримуємо
. (2)
У рівняння (2) підставляємо задані в умові задачі величини і отримуємо відповідь:
=
5. 34. Над площею
висить ліхтар. Освітленість у тих точках,
де промені
падають на землю під кутом
дорівнює 10 лк (
= 0,3). Яка
освітленість в точках, де промені падають
на землю під кутом
Рис. 5.34
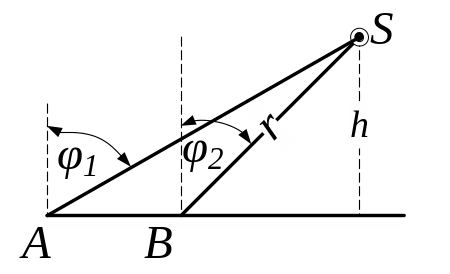
= 0,6)?
Р
Дано:
= 0,3
=
0,6
= 10 лк
= ?
Освітленість, яка створюється точковим ізотропним джерелом силою світла , що знаходиться на відстані від точки дорівнює
, (1)
де
- кут падіння променів на землю;
- відстань від джерела світла до точки
на землі.
Тоді отримаємо
. (2)
У рівняння (2) підставляємо задані в умові задачі величини і отримуємо відповідь:
=
5. 35. Круглий зал діаметром 30 м освітлюється лампою, яка прикріплена до центру стелі. Знайти висоту зали, якщо відомо, що найменша освітленість стіни залу в 2 рази більше найменшої освітленості підлоги?
Рис. 5.35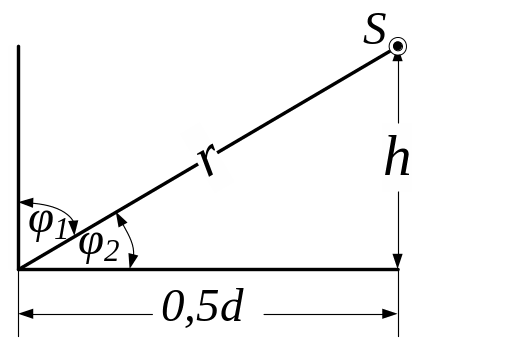
Р
Дано:
= 30
м
= ?
= 2
Освітленість, яка створюється точковим ізотропним джерелом силою світла , що знаходиться на відстані від точки дорівнює
, (1)
де
- кут падіння променів на поверхню;
- відстань від джерела світла до точок
на стіні та на підлозі;
.
Тоді отримаємо
. (2)
З рівняння (2) визначаємо висоту зали, підставляємо задані в умові задачі величини і отримуємо відповідь:
=
5. 36. Стіл діаметром 0,6 м освітлюється лампою, що висить на висоті 0, 4 м над центром столу. Яка освітленість краю столу, якщо повний світловий потік, що утворюється лампою становить 628 лм?
Рис. 5.36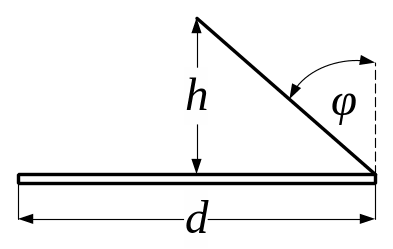
Р
Дано:
= 0,6
м
= 0,4 м
= 628 лм
= ?
Освітленість, яка створюється точковим ізотропним джерелом силою світла , що знаходиться на відстані від точки дорівнює
, (1)
де - кут падіння променів на стіл; - відстань від джерела світла до краю столу; - сила світла, що дорівнює світловому потоку , що розповсюджується в одиниці тілесного кута
;
.
Тоді отримаємо
. (2)
У рівняння (2) підставляємо задані в умові задачі величини і отримуємо відповідь:
=
5. 37. Площадка висвітлюється двома різними лампами, що висять на стовпі одна над одною на висоті 8 м та 27 м. На якій відстані від підстави стовпа знаходяться точки площадки, освітленість яких не зміниться, якщо поміняти лампи місцями?
Р
Дано:
= ?
= 8
м
= 27
м
О
Рис. 5.37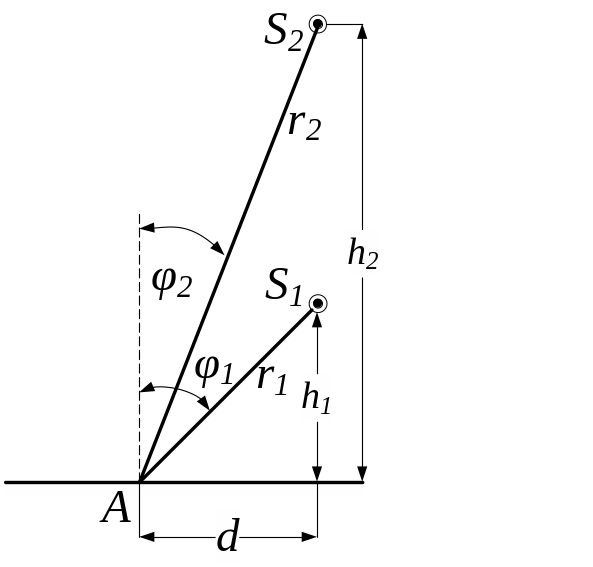
, (1)
де
- кут падіння променів;
- відстань від джерела світла до точки
;
.
Звідки отримуємо освітленість
у точці
від двох джерел
і
,які
знаходяться на відстанях
і
від підстави стовпа
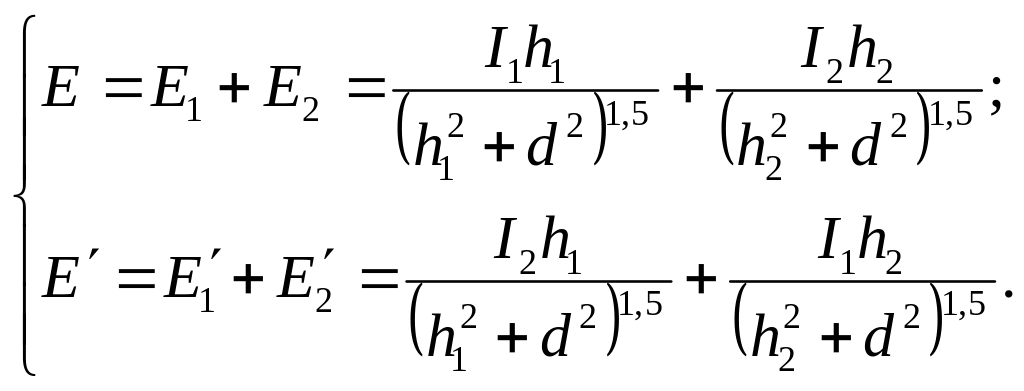. (2)
Оскільки
,
то отримаємо рівняння:
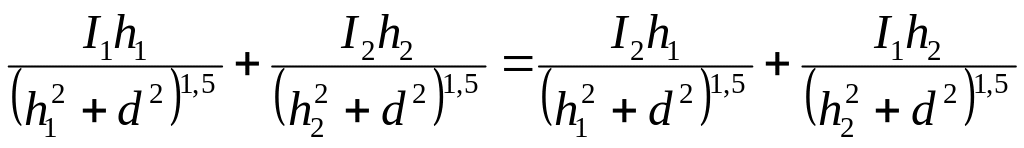. (3)
Звідки отримуємо
.
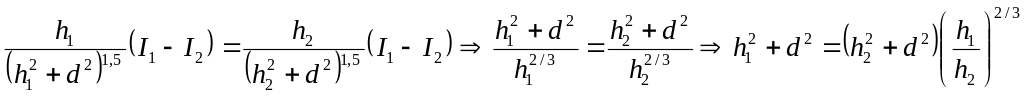(4)
З рівняння (4) маємо
.
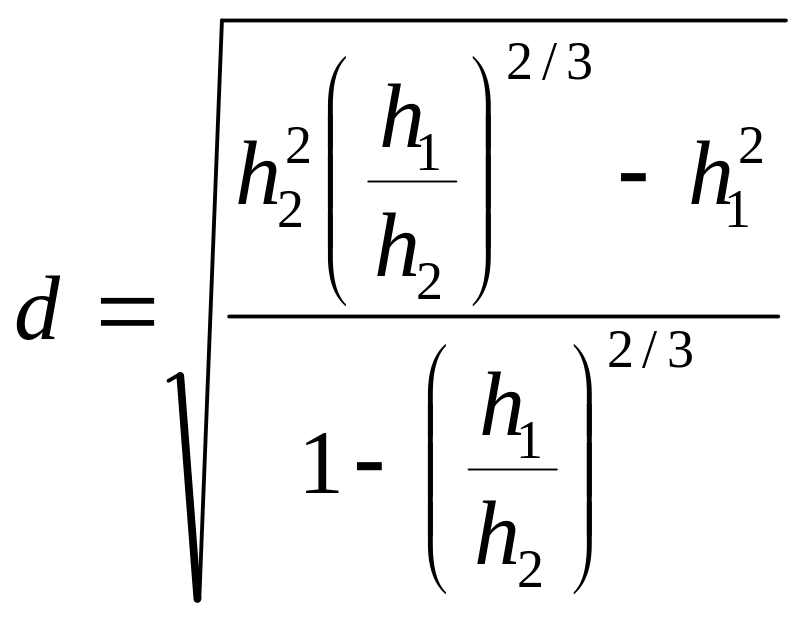(5)
У рівняння (4) підставляємо задані в умові задачі величини і отримуємо відповідь:
=
5. 38. Круглий зал діаметром 32 м освітлюється лампою, що закріплена в центрі стелі. Знайти висоту залу, якщо найменша освітленість стіни залу в два рази більше найменшої освітленості підлоги.
Р
Дано:
= 32
м
= 2
= ?
Рис. 5.38
Освітленість, яка створюється точковим ізотропним джерелом силою світла , що знаходиться на відстані від точки дорівнює
, (1)
де - кут падіння променів на поверхню; - відстань від джерела світла до точок на стіні та на підлозі; .
Тоді отримаємо
. (2)
З рівняння (2) визначаємо висоту зали, підставляємо задані в умові задачі величини і отримуємо відповідь:
=
5. 39. Над серединою столу на висоті 2 м висить лампа з силою світла 110 кд. її замінили на лампу у 17, 6 кд, зменшивши відстань до столу так, що освітленість середини столу залишилася незмінною. Знайти висоту на якій тепер висить лампа.
Рис. 5.39
Р
Дано:
= ?
= 2 м
= 110 кд
= 17,6 кд
Освітленість, яка створюється точковим ізотропним джерелом силою світла , що знаходиться на відстані від точки дорівнює
, (1)
де
- кут падіння променів на поверхню столу,
за умовою він дорівнює нулю;
- відстань від джерела світла до краю
столу;
- сила світла.
Тоді згідно з умовою задачі отримаємо
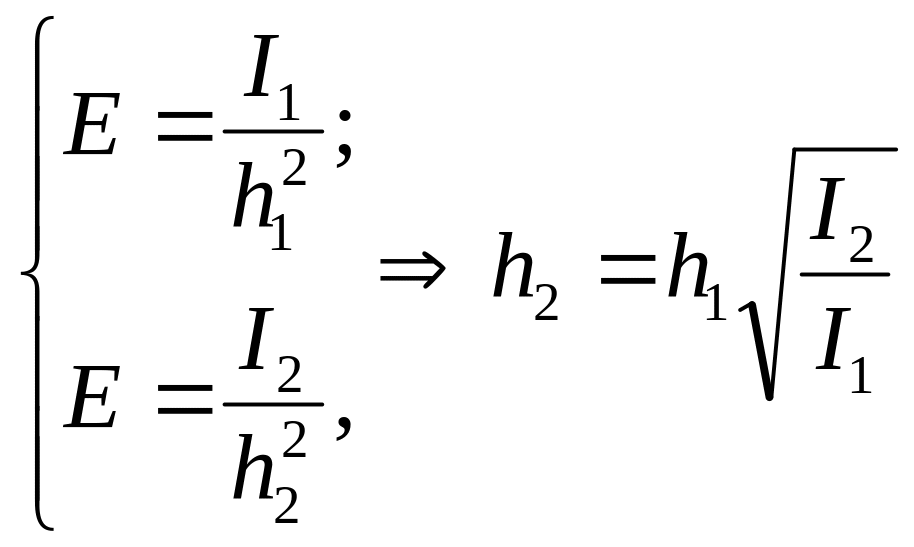. (2)
У рівняння (2) підставляємо задані в умові задачі величини і отримуємо відповідь:
=
5. 40. Знайти силу світла лампи вуличного освітлення необхідну для того, щоб освітленість землі посередині між ліхтарями була 0,2 лк. Лампи підвішені на висоті 4 м. Відстань між стовпами 6 м.
Рис. 5.40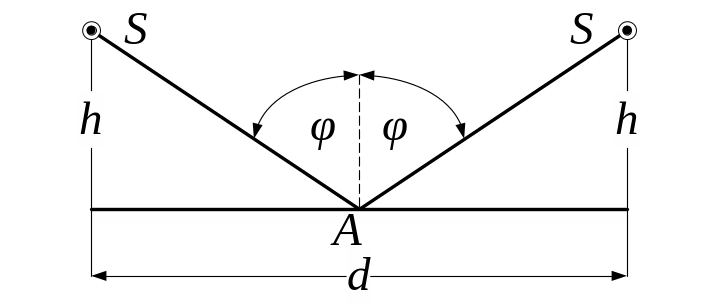
Р
Дано:
=
0,2 лк
= 4 м
= 6 м
= ?
Освітленість, яка створюється точковим ізотропним джерелом силою світла , що знаходиться на відстані від точки дорівнює
, (1)
де
- кут падіння променів на землю, за умовою
;
- відстань від джерела світла до середини
між стовпами;
- сила світла.
Тоді згідно з умовою задачі отримаємо
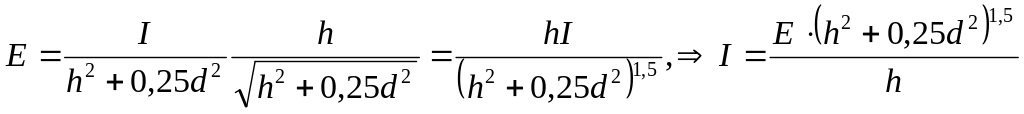. (2)
У рівняння (2) підставляємо задані в умові задачі величини і отримуємо відповідь:
=
5. 41. З якої найбільшої відстані можна помітити уночі вогник, якщо його сила світла 2,5 мкд, а найменший світловий потік, що сприймається оком людини 10-13 лм? Поверхня зіниці ока в темряві дорівнює 0,4 см2.
Розв’язок.
С
Дано:
= 2,5 мкд
= 10-13
лм
= ?
= 0,4
см2
, (1)
який дорівнює
.
Тоді рівняння (1) можна записати так
, (2)
У рівняння (2) підставляємо задані в умові задачі величини і отримуємо відповідь:
=
5. 42. На якій висоті над креслярською дошкою треба повісити лампу потужністю 400 Вт, щоб освітленість дошки під лампою склала 50 лк? Світловіддача лампи 12 лм/Вт. Нахил дошки до обрію 60°.
Розв’язок.
С
Дано:
= 50 лк
= 12 лм/Вт
= 60°
= ?
Рис. 5.42
= 400 Вт
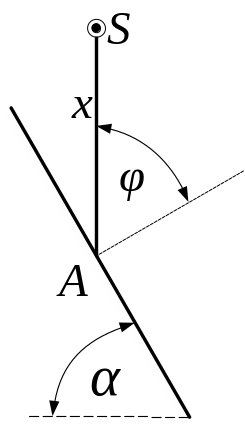
, (1)
який в нашому випадку дорівнює
повному тілесному куту
.
Повний потік дорівнює
.
Тоді рівняння (1) можна записати так
. (2)
Освітленість, яка створюється точковим ізотропним джерелом силою світла , що знаходиться на відстані від точки дорівнює
, (3)
де = - кут падіння променів на дошку.
У рівняння (3) підставляємо задані в умові задачі величини і отримуємо відповідь:
=
5. 43. По обидві боки від точкового джерела світла на відстанях 40 см, паралельно один одному знаходяться екран та плоске дзеркало. Знайти освітленість в центрі екрана, якщо сила світла джерела дорівнює 2,7 кд?
Рис. 5.39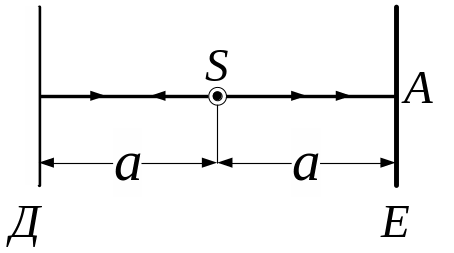
Р
Дано:
= 2,7 кд
= ?
= 40 см
Освітленість, яка створюється точковим ізотропним джерелом силою світла , що знаходиться на відстані від точки дорівнює
, (1)
де - кут падіння променів на землю, за умовою він дорівнює нулю.
Тоді згідно з умовою задачі отримаємо
. (2)
У рівняння (2) підставляємо задані в умові задачі величини і отримуємо відповідь:
=
5. 44. Над круглим столом, діаметром 160 см, на висоті 60 см висить лампочка, створюючи освітленість краю столу у 303 лк. Визначити силу світла лампочки.
Рис. 5.44
Р
Дано:
= 160
см
= 60 см
= 303 лк
= ?
Освітленість, яка створюється точковим ізотропним джерелом силою світла , що знаходиться на відстані від точки дорівнює
, (1)
де
- кут падіння променів на край столу;
- відстань від джерела світла до краю
столу;
.
Тоді отримаємо
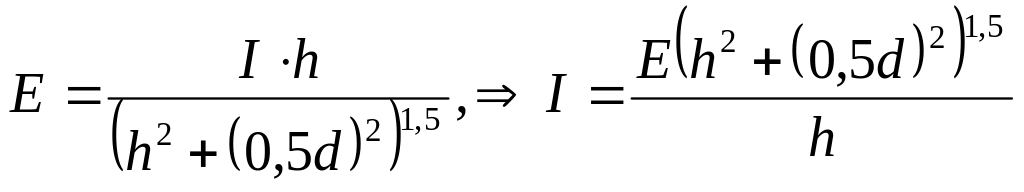. (2)
У рівняння (2) підставляємо задані в умові задачі величини і отримуємо відповідь:
=
5. 45. Над круглим столом, діаметром 240 см, на висоті 50 см висить лампочка. Визначить у скільки разів максимальна освітленість точок на поверхні столу перевищує мінімальну.
Рис. 5.44
Р
Дано:
= 240
см
= 50 см
= ?
Освітленість, яка створюється точковим ізотропним джерелом силою світла , що знаходиться на відстані від точки дорівнює
, (1)
де - кут падіння променів на поверхню столу; - відстань від джерела світла до краю столу; .
Тоді отримаємо
. (2)
У рівняння (2) підставляємо задані в умові задачі величини і отримуємо відповідь:
=
5. 46. По обидві боки від точкового джерела світла на відстанях 40 см, паралельно один одному знаходяться екран та плоске дзеркало, освітленість в центрі екрана дорівнює 18,75 лк. Знайти силу світла джерела.
Рис. 5.46
Р
Дано:
= 40 см
= 18,75 лк
= ?
Освітленість, яка створюється точковим ізотропним джерелом силою світла , що знаходиться на відстані від точки дорівнює
, (1)
де - кут падіння променів на екран, за умовою він дорівнює нулю.
Тоді згідно з умовою задачі отримаємо
. (2)
У рівняння (2) підставляємо задані в умові задачі величини і отримуємо відповідь:
=
5. 47. Максимальна освітленість точок на поверхні круглого столу діаметром 240 см перевищує мінімальну у 17,576 разів. На якій висоті над центром столу висить лампочка?
Рис. 5.47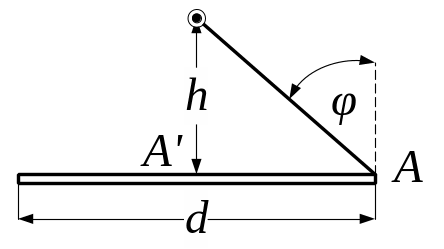
Р
Дано:
= 240
см
= 17,576
= ?
Освітленість, яка створюється точковим ізотропним джерелом силою світла , що знаходиться на відстані від точки дорівнює
, (1)
де
- кут падіння променів на поверхню столу;
- відстань від джерела світла до краю
столу;
.
Тоді отримаємо
. (2)
У рівняння (2) підставляємо задані в умові задачі величини і отримуємо відповідь:
=
5. 48. Над центром круглого столу на висоті 50 см висить лампочка. Максимальна освітленість точок на поверхні столу перевищує мінімальну у 17,576 разів. Знайти діаметр столу.
Рис. 5.48
Р
Дано:
= 50 см
= 17,576
= ?
Освітленість, яка створюється точковим ізотропним джерелом силою світла , що знаходиться на відстані від точки дорівнює
, (1)
де - кут падіння променів на стіл; - відстань від джерела світла до краю столу; .
Тоді отримаємо
. (2)
У рівняння (2) підставляємо задані в умові задачі величини і отримуємо відповідь:
=
5. 49. Над центром квадратного столу на висоті, яка дорівнює стороні квадрата, висить лампочка. У скільки разів максимальна освітленість точок на поверхні столу перевищує мінімальну.
Р
Дано:
=
= ?
Рис. 5.49
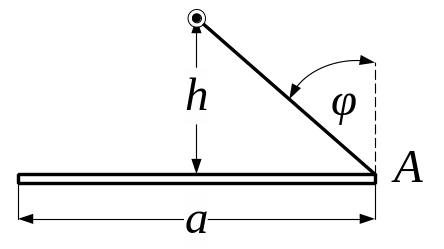
Освітленість, яка створюється точковим ізотропним джерелом силою світла , що знаходиться на відстані від точки дорівнює
, (1)
де
- кут падіння променів на стіл;
- відстань від джерела світла до краю
столу;
.
Тоді отримаємо
. (2)
У рівняння (2) підставляємо задані в умові задачі величини і отримуємо відповідь:
=
5. 50. Над майданом на висоті 5 метрів висить точкове джерело світла силою 200 кд. Знайти площу поверхні, всередині якої освітленість майдану буде не менша 1 лк
Рис. 5.50
Р
Дано:
= 5 м
= 200 кд
= 1 лк
= ?
Вважаємо, що поверхня, освітленість якої буде відповідати умові задачі дорівнює площі, яка обмежена колом з діаметром .
Освітленість, яка створюється точковим ізотропним джерелом силою світла , що знаходиться на відстані від точки дорівнює
, (1)
де - кут падіння променів на стіл; - відстань від джерела світла до краю столу; .
Тоді отримаємо
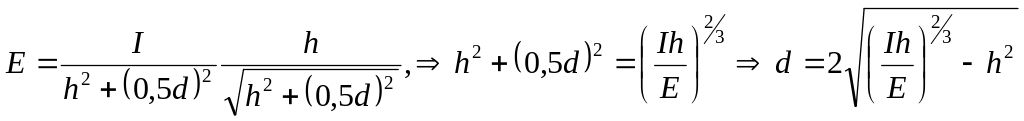. (2)
Тоді відповідь дорівнює
. (3)
У рівняння (3) підставляємо задані в умові задачі величини і отримуємо відповідь:
=